RobustConvexOptimization
RobustConvexOptimization[f,ForAll[pars,pcons,vcons],vars]
パラメータ的な制約 pcons を満足するパラメータ pars の可能なすべての値について制約 vcons を満足する vars についての f の最小値を与える vars の値を求める.
RobustConvexOptimization[…,"prop"]
解のどの特性"prop"を返すかを指定する.
詳細とオプション




- ロバスト最適化は最悪な場合の最適化としても知られている.
- ロバスト最適化は,一般に,パラメータ制約があるパラメータによって表される不確かさのもとで最適化問題を解く際に使われる.
- ロバスト最適化は,与えられた最適条件には可能なすべてのパラメータ値で達することができるという意味で,最も保守的な解を与える.
- ロバスト最適化は,以下の問題を解くロバストなミニマイザ
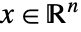 を求める.
を求める. -
最小化 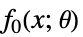
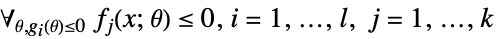
ただし 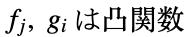
- ロバストミニマイザ
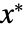 は,パラメータ集合内のすべての
は,パラメータ集合内のすべての 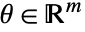 について
について 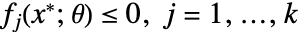 を満足する.
を満足する. - ロバスト最小値
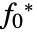 は,パラメータ集合内のすべての
は,パラメータ集合内のすべての 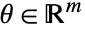 について
について 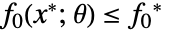 を満足する.
を満足する. - pcons または vcons には,線形等式制約
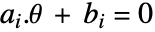 または
または 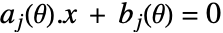 が含まれるかもしれない.
が含まれるかもしれない. - RobustConvexOptimization[f,cons,vars,pars]を使うこともできる.制約条件 cons は純粋にパラメータ的な制約条件
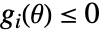 とパラメータ
とパラメータ 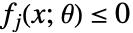 に依存する変数の制約条件に自動的に分離される.この形式はParametricConvexOptimizationと互換である.
に依存する変数の制約条件に自動的に分離される.この形式はParametricConvexOptimizationと互換である. - ロバスト最適化問題は,可解のあるいは凸最適化で近似可能な問題の型にはめられる場合は扱いやすいと考えられる.扱いやすさは変数制約
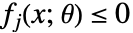 のタイプとパラメータ制約
のタイプとパラメータ制約 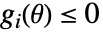 のタイプの組合せに依存する.
のタイプの組合せに依存する. - 次の変数制約とパラメータ制約の組合せが扱いやすいと考えられる.
-
変数制約 パラメータ制約 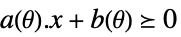
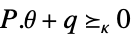
![TemplateBox[{{{a, ., x}, +, b}}, Norm]<=c(theta).x+d(theta) TemplateBox[{{{a, ., x}, +, b}}, Norm]<=c(theta).x+d(theta)](Files/RobustConvexOptimization.ja/19.png)
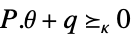
![TemplateBox[{{{{a, (, theta, )}, ., x}, +, {b, (, theta, )}}}, Norm]<=c.x+d TemplateBox[{{{{a, (, theta, )}, ., x}, +, {b, (, theta, )}}}, Norm]<=c.x+d](Files/RobustConvexOptimization.ja/21.png)
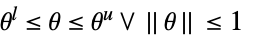
![TemplateBox[{{{{a, (, {theta, _, l}, )}, ., x}, +, {b, (, {theta, _, l}, )}}}, Norm]<=c(theta_r).x+d(theta_r) TemplateBox[{{{{a, (, {theta, _, l}, )}, ., x}, +, {b, (, {theta, _, l}, )}}}, Norm]<=c(theta_r).x+d(theta_r)](Files/RobustConvexOptimization.ja/23.png)
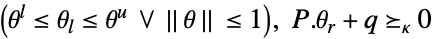
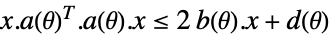
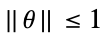
![a_0(theta)+a_1(theta) x_1+...+a_k(theta) x_k>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_0(theta)+a_1(theta) x_1+...+a_k(theta) x_k>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/RobustConvexOptimization.ja/27.png)
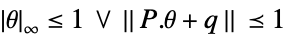
- 一般に,変数制約
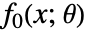 は
は 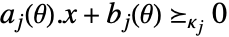 の形の円錐制約に変換される.ただし,
の形の円錐制約に変換される.ただし,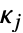 は,"NonNegativeCone","NormCone","SemidefiniteCone"のいずれかであり,
は,"NonNegativeCone","NormCone","SemidefiniteCone"のいずれかであり,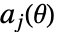 と
と 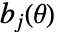 のパラメータに対する依存関係はアフィンでなければならない.
のパラメータに対する依存関係はアフィンでなければならない. - 目的関数
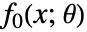 がパラメータに依存する,あるいは非線形である場合は,追加的な変数
がパラメータに依存する,あるいは非線形である場合は,追加的な変数 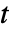 が導入され,エピグラフ変換によって,問題が目的変数
が導入され,エピグラフ変換によって,問題が目的変数 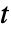 と追加的な制約条件
と追加的な制約条件 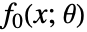 を持つようになる.
を持つようになる. - 変数指定とパラメータ指定の vars と pars は,それぞれ,以下のいずれかの形で変数とパラメータを与える要素のリストでなければならない.
-
v 次元が推測される変数か名前が 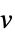 のスカラーパラメータ
のスカラーパラメータv∈Reals 実数のスカラー変数 v∈Integers 整数のスカラー変数 v∈Complexes 複素数のスカラー変数 v∈ℛ 幾何学領域 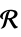 に制限されるベクトル変数
に制限されるベクトル変数v∈Vectors[n,dom] 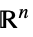 ,
,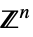 あるいは
あるいは![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/RobustConvexOptimization.ja/42.png) のベクトル変数
のベクトル変数v∈Matrices[{m,n},dom] 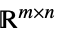 ,
,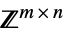 あるいは
あるいは![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/RobustConvexOptimization.ja/45.png) の行列変数
の行列変数 - 使用可能な解の特性"prop"には以下がある.
-
"PrimalMinimizer" 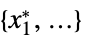
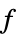 を最小化する変数値のリスト
を最小化する変数値のリスト"PrimalMinimizerRules" 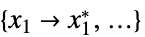
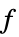 を最小化する変数 vars={v1,…}の値
を最小化する変数 vars={v1,…}の値"PrimalMinimizerVector" 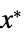
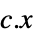 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 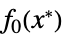
最小値 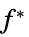
{"prop1","prop2",…} いくつかの解の特性 - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する最大反復数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal 最適化するパフォーマンスの局面 Tolerance Automatic 内部比較の許容度 - オプションMethodmethod を使って使用するメソッドが指定できる.以下は使用可能なメソッドである.
-
Automatic メソッドを自動的に選択する "CuttingSet" CuttingSet法を使う "PolyhedralApproximation" 線形制約集合がある近似"NormCone"制約 "SCS" SCS(錐ソルバの分割)ライブラリ "CSDP" CSDP(COIN半定値計画)ライブラリ "DSDP" DSDP(半定値計画)ライブラリ - いくつかの扱いにくいロバストな最適化問題も,ほぼCuttingSet法で解くことができる.
例題
すべて開くすべて閉じる例 (2)
スコープ (29)
基本的な用法 (15)
![]() のとき,すべての
のとき,すべての ![]() について,
について,![]() についての
についての ![]() に従うロバストなミニマイザを求める:
に従うロバストなミニマイザを求める:
区間![]() 内のすべての
内のすべての ![]() について,
について,![]() についての
についての ![]() に従うロバストなミニマイザを求める:
に従うロバストなミニマイザを求める:
![]() となるようなすべての
となるようなすべての ![]() について,
について,![]() に従う
に従う ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
![]() のとき,すべての
のとき,すべての![]() について
について ![]() に従う
に従う ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
明示的なForAllなしで代替構文を使う:
この構文をParametricConvexOptimizationで直接使って![]() の特定の値を試してみる:
の特定の値を試してみる:
VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表す:
VectorGreaterEqualを使っていくつかのGreaterEqual不等式制約を一度に表す:
スカラー不等式とベクトル不等式を組み合せて制約条件を指定する:
![]() であるすべての
であるすべての![]() について,制約条件
について,制約条件 ![]() に従って関数
に従って関数 ![]() を最小化する:
を最小化する:
Indexedを使ってベクトル変数の成分(例:![]() )にアクセスする:
)にアクセスする:
制約条件のパラメータ方程式を使って目的関数と制約条件の係数を指定する:
![]() であるすべての
であるすべての ![]() について,制約条件
について,制約条件 ![]() に従って関数
に従って関数 ![]() を最小にする:
を最小にする:
必要なときは,Vectors[n,Reals]を使ってベクトル変数の次元を指定する:
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
NonPositiveReals (![]() )を使って非正の制約条件を指定する:
)を使って非正の制約条件を指定する:
Intervalを使って境界を指定する:
パラメータがグループ化され変数に割り当てられたときに,Evaluateを使ってForAllの第1引数が確実に評価されるようにする:
線形変数制約 (5)
区間[0,2]内のすべての ![]() について,
について,![]() に従う
に従う ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
[0,2]内のすべての ![]() についての制約条件
についての制約条件 ![]() とは,数学的には
とは,数学的には ![]() を意味する.従って,この問題は以下と等しい:
を意味する.従って,この問題は以下と等しい:
区間で制限されるすべての![]() について,変数の制約条件
について,変数の制約条件 ![]() に従って
に従って ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
![]() の極値に設定されたミニマイザと変数制約を可視化する.緑で示されているパラメータ
の極値に設定されたミニマイザと変数制約を可視化する.緑で示されているパラメータ ![]() の可能なすべての値に対して実行可能である
の可能なすべての値に対して実行可能である![]() の集合は,パラメトリック実行可能領域の交点である:
の集合は,パラメトリック実行可能領域の交点である:
区間に制約されるすべての![]() について,変数制約条件
について,変数制約条件 ![]() に従う
に従う ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
ミニマイザ,パラメータ ![]() の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
![]() であるすべての
であるすべての![]() について,変数制約
について,変数制約 ![]() に従う
に従う ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
ミニマイザ,パラメータ ![]() の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
![]() であるすべての
であるすべての![]() について,変数制約
について,変数制約 ![]() に従う
に従う ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
NormCone変数制約 (7)
![]() であるすべての
であるすべての ![]() についての変数制約
についての変数制約![]() 上の
上の ![]() についてのロバストミニマイザを求める:
についてのロバストミニマイザを求める:
![]() の極値に設定されたミニマイザと変数制約を可視化する.パラメータ
の極値に設定されたミニマイザと変数制約を可視化する.パラメータ ![]() の可能なすべての値に対して実行可能な
の可能なすべての値に対して実行可能な![]() の集合は,全実行可能領域の共通部分(緑色で表示)である:
の集合は,全実行可能領域の共通部分(緑色で表示)である:
![]() であるすべての
であるすべての ![]() についての変数制約
についての変数制約![]() 上の
上の ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
ミニマイザ,パラメータ ![]() の極値に設定された変数制約,実行可能領域(緑色で表示)を可視化する:
の極値に設定された変数制約,実行可能領域(緑色で表示)を可視化する:
![]() であるすべての
であるすべての ![]() についての変数制約
についての変数制約![]() 上の
上の ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
ミニマイザ,![]() の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
![]() であるすべての
であるすべての ![]() についての変数制約
についての変数制約![]() 上の
上の ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
ミニマイザ,![]() の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
![]() であるすべての
であるすべての ![]() についての変数制約
についての変数制約![]() 上の
上の ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
![]() であるすべての
であるすべての ![]() についての変数制約
についての変数制約![]() 上の
上の ![]() についてのロバストなミニマイザを求める:
についてのロバストなミニマイザを求める:
ミニマイザ,![]() の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
の極値についての変数制約集合,実行可能領域(緑で表示)を可視化する:
オプション (3)
Method (2)
アプリケーション (14)
幾何学問題 (2)
データフィッティング問題 (3)
区間の不確かさに従って,応答があるデータのロバストな線形フィットを求める:
目的は,区間の不確かさ ![]() に従って入出力間の誤差を最小にすることである:
に従って入出力間の誤差を最小にすることである:
ロバストなフィット y=m x+b の傾き m と切片 b を求める:
不確かさの100の可能な実現のためのフィットモデルを求める:
ロバストフィット(黒),単純フィット(緑),データで,フィットモデルの包絡線を表示する:
出力に区間の不確かさ![]() が含まれる離散データに三次曲線をフィットする:
が含まれる離散データに三次曲線をフィットする:
DesignMatrixを使って入力行列を構築する:
目的は区間の不確かさ ![]() に従って入出力間の誤差を最小にすることである:
に従って入出力間の誤差を最小にすることである:
不確かさの可能な100の実現についてのフィットモデルを求める:
フィットモデルの包絡線を,ロバストなフィット(黒)およびデータとともに表示する:
ロバストなフィット(黒)と平均モデル(赤)をノイズのない厳密解と比較する:
ロバストなフィットは平均モデルよりも誤差が大きくなる傾向がある:
測定のインスタンス(入力)が不確かな範囲![]() にある離散データに三次曲線をフィットする:
にある離散データに三次曲線をフィットする:
製造問題 (3)
2つの異なる原材料 ![]() から活性剤を抽出する際の不確かさを考慮して利益を最大化するためにある会社が製造する2つの薬剤
から活性剤を抽出する際の不確かさを考慮して利益を最大化するためにある会社が製造する2つの薬剤 ![]() の最適な組合せを求める.医薬品の単位あたりの収益は以下の通りである:
の最適な組合せを求める.医薬品の単位あたりの収益は以下の通りである:
2つの薬の製造には90から100時間の人的資源が必要である.同社の人的資源は2000時間分しかない:
2つの薬を製造するのに40から50時間の機械時間が必要である.同社の機械時間は800時間しかない:
2つの薬を製造するための運用コストはそれぞれ700と800である.キログラムあたりの原材料費はそれぞれ100と199.9である:
同社は数単位の薬を製造しなければならず,したがってある程度の原材料を購入しなければならない:
2つの原材料から抽出される活性剤の量は,それぞれ![]() g/kgおよび
g/kgおよび![]() g/kgの原材料である.2つの薬はそれぞれ0.5g /単位と0.6g /単位の活性剤を必要とする:
g/kgの原材料である.2つの薬はそれぞれ0.5g /単位と0.6g /単位の活性剤を必要とする:
目的は,購入コストと運用コストを最小限に抑えながら収益を最大化することである:
原材料に活性剤の変動がない場合は,2番目の原材料が優先される:
ロバストな解は,原材料から抽出される活性剤の量が最も少ないという最悪のシナリオに対応する:
ロバストな解を使用する利点を確認するために,原材料と活性剤の不確かさをパラメータとして使ってパラメトリック関数を生成する:
名目上の結果,つまり ![]() を使用して原材料を購入した場合,原材料から抽出できる活性剤の量によっては,利益が21%減少する可能性がある:
を使用して原材料を購入した場合,原材料から抽出できる活性剤の量によっては,利益が21%減少する可能性がある:
原材料がロバストな結果を使用して購入された場合,つまり,![]() の場合,利益は最大6%減少する可能性がある:
の場合,利益は最大6%減少する可能性がある:
2番目の原材料から抽出できる活性剤の関数として利益をプロットする:
製造入力に不確かさがある企業の利益を最大化する製造製品の組合せを求める.同社は3つの製品を製造している.理想的な条件下では,単位あたりの収益,単位あたりのコスト,最大容量は次の式で与えられる:
各製品は4台の機械を使用して作られる.機械が各製品に費やす時間は次の通りである:
市場の変動のために,製品の各単位によって生成される収益は5ドル減少する可能性がある:
機械のダウンタイムを考慮すると,製造能力は製品ごとに5ユニット減少する可能性がある:
各機械は週に最大2400分実行できる.機械が稼働していない場合,稼働状態に戻るまでに最大120分かかる:
4台の機械のいずれかを修理するためのコストは,各製品のコストを1単位あたり5ドル増加させる:
利益は収益からコストを引いたものに製品 ![]() の単位数
の単位数 ![]() を掛けたものに等しくなる:
を掛けたものに等しくなる:
目的は,収益を最大にすることである.最適な製品の組合せは以下で与えられる:
さまざまなパラメータを変更するためのパラメトリック関数を作成する:
最良のシナリオでは,収益の減少や機械のダウンタイムは発生せず,以下のようになる:
最悪のシナリオは,RobustConvexOptimizationによって得られた結果に対応する:
価格と供給の変動に応じて3つの製品 ![]() を販売する会社の利益を最大化する製造製品の組合せを求める.
を販売する会社の利益を最大化する製造製品の組合せを求める.
単位あたり![]() の価格変動を考慮した単位あたりの収益は以下の通りである:
の価格変動を考慮した単位あたりの収益は以下の通りである:
この工場は100日しか稼働しない.理想的には,各単位の製造に2,4,5日かかるが,予期しない遅延により製造時間が1日長くなる可能性がある:
各製品には金と錫が含まれている.各単位で使用可能な金と錫は,それぞれ![]() および
および![]() である:
である:
製品が製造された場合,会社は各製品のセットアップ費用を負担する:
セットアップ費用が比較的高いため,一部の製品を全く製造しないことが望ましい場合がある.![]() を,製品
を,製品 ![]() が製造されている場合は
が製造されている場合は ![]() ,それ以外の場合は
,それ以外の場合は ![]() となる決定変数とする.制限
となる決定変数とする.制限 ![]() は他の制約よりも
は他の制約よりも ![]() のサイズを制限することなく,
のサイズを制限することなく,![]() が0の場合は
が0の場合は ![]() も0であることを保証する:
も0であることを保証する:
構造最適化問題 (1)
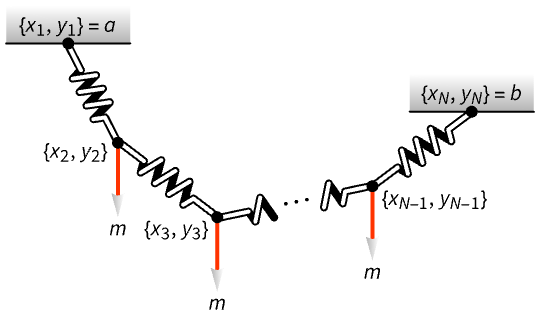
バネの剛性と平衡長の両方が製造上の不確かさの影響を受ける各リンクの端に垂直荷重がかかった状態で,![]() のバネリンクによって形成される吊り下げチェーンの形状を求める.目的はリンクの位置
のバネリンクによって形成される吊り下げチェーンの形状を求める.目的はリンクの位置 ![]() を求めることである:
を求めることである:
重力による位置エネルギーは ![]() である.ただし,
である.ただし,![]() は両端の垂直荷重,
は両端の垂直荷重,![]() は重力である:
は重力である:
伸縮によるバネリンクの張力による位置エネルギーは ![]() である.ここで,
である.ここで,![]() はバネリンク
はバネリンク ![]() の伸縮,
の伸縮,![]() はバネの不確かな剛性であり,
はバネの不確かな剛性であり,![]() はバネの理想的な剛性である.
はバネの理想的な剛性である.![]() を使用してエネルギーを
を使用してエネルギーを ![]() に変換する:
に変換する:
リンクチェーンの端は(0,0)と(2,-1)に固定されている:
各リンクは制約条件![]() を満足しなければならない.ただし,
を満足しなければならない.ただし,![]() は不確かさ
は不確かさ ![]() に従う各バネの静止長である:
に従う各バネの静止長である:
ポートフォリオの最適化 (2)
平均リターンに不確実性がある場合にリスクを最小限に抑えながらリターンを最大化するために,市場のボラティリティの影響を受ける可能性のある20の候補株から投資する6つの株の最適な組合せを見付ける.株式 ![]() の期待収益値
の期待収益値 ![]() および株式
および株式 ![]() 間の共分散は次の通りである:
間の共分散は次の通りである:
市場の変動のために各株式の平均収益値は不確実性 ![]() の影響を受ける:
の影響を受ける:
![]() は
は ![]() ならばその株を買うことになる決定ベクトルであるとすると,6つの株を選択しなければならない:
ならばその株を買うことになる決定ベクトルであるとすると,6つの株を選択しなければならない:
リスクを最小にしてリターンを最大にする株の最適な組合せを求める:
さまざまなパラメータを変更するためのパラメトリック関数を作成する:
最も安全で最適な株式の組合せは,不確実性のランダムなインスタンスを持つ最適な株式と比較して,最小のリスクとリターンを提供する:
平均リターンと共分散の両方に不確実性がある場合に,リスクを最小化しながらリターンを最大化するためのに6つの株に投資する資本の分布を見付ける.株 ![]() の期待収益値
の期待収益値 ![]() および株
および株 ![]() 間の共分散は次の通りである:
間の共分散は次の通りである:
市場の変動のために,各株式のリターン値は不確実性 ![]() の影響を受ける:
の影響を受ける:
共分散は有限のデータ集合から抽出され,不確実性 ![]() の影響を受ける:
の影響を受ける:
目的は,指定されたリスク回避パラメータ ![]() のリスクを最小限に抑えながらリターンを最大にすることである:
のリスクを最小限に抑えながらリターンを最大にすることである:
施設の場所問題 (1)
分類問題 (2)
2つの点集合![]() と
と ![]() を分離する線分
を分離する線分 ![]() を求める.ただし,
を求める.ただし,![]() は区間の不確かさである:
は区間の不確かさである:
分離するために,集合1は ![]() を,集合2は
を,集合2は ![]() を満足しなければならない:
を満足しなければならない:
目的は![]() を最小化することである.これによって
を最小化することである.これによって ![]() と
と ![]() の間の最大の厚さが得られる:
の間の最大の厚さが得られる:
不確かさが大きくなった集合を可視化すると,2つの集合に不確かさのボックスが重なるいくつかの点があることが分かる:
2つの3Dの点集合 ![]() と
と ![]() を分離する二次多項式を求める.ただし,
を分離する二次多項式を求める.ただし,![]() は不確かさの区間である:
は不確かさの区間である:
DesignMatrixを使って2つの集合のために二次多項式データ行列を構築する:
テキスト
Wolfram Research (2020), RobustConvexOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/RobustConvexOptimization.html.
CMS
Wolfram Language. 2020. "RobustConvexOptimization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RobustConvexOptimization.html.
APA
Wolfram Language. (2020). RobustConvexOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RobustConvexOptimization.html

