ConvexOptimization[f,cons,vars]
finds values of variables vars that minimize the convex objective function f subject to convex constraints cons.
ConvexOptimization[…,"prop"]
specifies what solution property "prop" should be returned.




ConvexOptimization
ConvexOptimization[f,cons,vars]
finds values of variables vars that minimize the convex objective function f subject to convex constraints cons.
ConvexOptimization[…,"prop"]
specifies what solution property "prop" should be returned.
Details and Options





- Convex optimization is global nonlinear optimization for convex functions with convex constraints. For convex problems, the global solution can be found.
- Convex optimization includes many other forms of optimization, including linear optimization, linear-fractional optimization, quadratic optimization, second-order cone optimization, semidefinite optimization and conic optimization.
- If
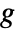 is concave, ConvexOptimization[-g,cons,vars] will maximize g.
is concave, ConvexOptimization[-g,cons,vars] will maximize g. - Convex optimization finds
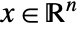 that solves the following problem:
that solves the following problem: -
minimize 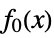
subject to constraints 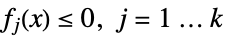
where 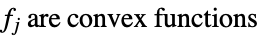
- Equality constraints of the form
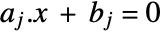 may be included in cons.
may be included in cons. - Mixed-integer convex optimization finds
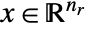 and
and 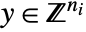 that solve the problem:
that solve the problem: -
minimize 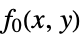
subject to constraints 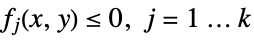
where 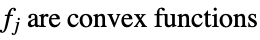
- When the objective function is real valued, ConvexOptimization solves problems with
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/ConvexOptimization.en/12.png) by internally converting to real variables
by internally converting to real variables 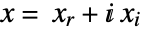 , where
, where 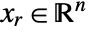 and
and 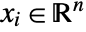 .
. - The variable specification vars should be a list with elements giving variables in one of the following forms:
-
v variable with name 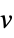 and dimensions inferred
and dimensions inferredv∈Reals real scalar variable v∈Integers integer scalar variable v∈Complexes complex scalar variable v∈ℛ vector variable restricted to the geometric region 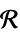
v∈Vectors[n,dom] vector variable in 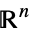 ,
, 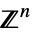 or
or ![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/ConvexOptimization.en/20.png)
v∈Matrices[{m,n},dom] matrix variable in 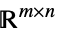 ,
, 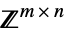 or
or ![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/ConvexOptimization.en/23.png)
- ConvexOptimization automatically does transformations necessary to find an efficient method to solve the minimization problem.
- The primal minimization problem as solved has a related maximization problem that is the Lagrangian dual problem. The dual maximum value is always less than or equal to the primal minimum value, so it provides a lower bound. The dual maximizer provides information about the primal problem, including sensitivity of the minimum value to changes in the constraints.
- The possible solution properties "prop" include:
-
"PrimalMinimizer" 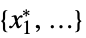
a list of variable values that minimizes 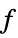
"PrimalMinimizerRules" 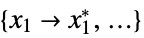
values for the variables vars={v1,…} that minimize 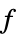
"PrimalMinimizerVector" 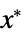
the vector that minimizes 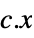
"PrimalMinimumValue" 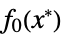
the minimum value 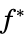
"DualMaximizer" 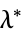
the vectors that maximize the dual problem "DualMaximumValue" the dual maximum value "DualityGap" 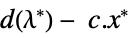
the difference between the dual and primal optimal values "Slack" 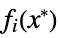
vectors that convert inequality constraints to equality {"prop1","prop2",…} several solution properties - The following options may be given:
-
MaxIterations Automatic maximum number of iterations to use Method Automatic the method to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize Tolerance Automatic the tolerance to use for internal comparisons WorkingPrecision MachinePrecision precision to use in internal computations - The option Methodmethod may be used to specify the method to use. Available methods include:
-
Automatic choose the method automatically solver transform the problem, if possible, to use solver to solve the problem "SCS" SCS splitting conic solver "CSDP" CSDP semidefinite optimization solver "DSDP" DSDP semidefinite optimization solver "MOSEK" commercial MOSEK convex optimization solver "Gurobi" commercial Gurobi linear and quadratic optimization solver "Xpress" commercial Xpress linear and quadratic optimization solver - Methodsolver may be used to specify that a particular solver is used so that the dual formulation used corresponds to the formulation documented for solver. Possible solvers are LinearOptimization, LinearFractionalOptimization, QuadraticOptimization, SecondOrderConeOptimization, SemidefiniteOptimization, ConicOptimization and GeometricOptimization.
Examples
open all close allBasic Examples (2)
Scope (28)
Basic Uses (12)
Minimize ![]() subject to the constraints
subject to the constraints ![]() and
and ![]() :
:
Several linear inequality constraints can be expressed with VectorGreaterEqual:
Use ![]() v>=
v>=![]() or \[VectorGreaterEqual] to enter the vector inequality sign :
or \[VectorGreaterEqual] to enter the vector inequality sign :
An equivalent form using scalar inequalities:
The inequality ![]() may not be the same as
may not be the same as ![]() due to possible threading in
due to possible threading in ![]() :
:
To avoid unintended threading in ![]() , use Inactive[Plus]:
, use Inactive[Plus]:
Use constant parameter equations to avoid unintended threading in ![]() :
:
VectorGreaterEqual represents a conic inequality with respect to the "NonNegativeCone":
To explicitly specify the dimension of the cone, use {"NonNegativeCone",n}:
Minimize ![]() subject to the constraint
subject to the constraint ![]() :
:
Specify the constraint ![]() using a conic inequality with "NormCone":
using a conic inequality with "NormCone":
Minimize ![]() subject to the positive semidefinite matrix constraint
subject to the positive semidefinite matrix constraint ![]() :
:
Use a vector variable ![]() and Indexed[x,i] to specify individual components:
and Indexed[x,i] to specify individual components:
Use Vectors[n,Reals] to specify the dimension of a vector variable when it may be ambiguous:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
An equivalent form using vector inequality ![]() :
:
Maximize the area of a rectangle with perimeter at most 1 and height at most half the width:
When ![]() and
and ![]() are positive, the problem can be solved by GeometricOptimization methods:
are positive, the problem can be solved by GeometricOptimization methods:
Using method GeometricOptimization implicitly assumes positivity:
Integer Variables (4)
Specify integer variables using Integers:
Specify integer domain constraints on vector variables using Vectors[n,Integers]:
Specify non-negative integer domain constraints using NonNegativeIntegers (![]() ):
):
Specify non-positive integer domain constraints using NonPositiveIntegers (![]() ):
):
Complex Variables (8)
Specify complex variables using Complexes:
Minimize a real objective ![]() with complex variables and complex constraints
with complex variables and complex constraints ![]() :
:
Let ![]() . Expanding out the constraints into real components gives:
. Expanding out the constraints into real components gives:
Solve the problem with real-valued objective and complex variables and constraints:
Solve the same problem with real variables and constraints:
Use a quadratic objective ![]() with Hermitian matrix
with Hermitian matrix ![]() and real-valued variables:
and real-valued variables:
Use objective (1/2)Inactive[Dot][Conjugate[x],q,x] with a Hermitian matrix ![]() and complex variables:
and complex variables:
Use a quadratic constraint ![]() with Hermitian matrix
with Hermitian matrix ![]() and real-valued variables:
and real-valued variables:
Use constraint (1/2)Inactive[Dot][Conjugate[x],q,x]d with a Hermitian matrix ![]() and complex variables:
and complex variables:
Find the Hermitian matrix with minimum 2-norm (largest singular value) such that the matrix ![]() is positive semidefinite:
is positive semidefinite:
The minimum for the largest singular value is:
Use a linear matrix inequality constraint ![]() with Hermitian or real symmetric matrices:
with Hermitian or real symmetric matrices:
The variables in linear matrix inequalities need to be real for the sum to remain Hermitian:
Primal Model Properties (1)
Dual Model Properties (3)
The dual problem is to maximize ![]() subject to
subject to ![]() :
:
The primal minimum value and the dual maximum value coincide because of strong duality:
That is the same as having a duality gap of zero. In general, ![]() at optimal points:
at optimal points:
Get the dual maximum value and dual maximizer directly using solution properties:
The "DualMaximizer" can be obtained with:
The dual maximizer vector partitions match the number and dimensions of the dual cones:
To get the dual format for a particular problem-type solver, specify it as a method option:
Options (13)
Method (8)
"SCS" is a splitting conic solver method:
"CSDP" is an interior point method for semidefinite problems:
"DSDP" is an alternative interior point method for semidefinite problems:
"IPOPT" is an interior point method for nonlinear problems:
Different methods have different default tolerances, which affects the accuracy and precision:
Compute exact and approximate solutions:
"SCS" has a default tolerance of ![]() :
:
"CSDP", "DSDP" and "IPOPT" have default tolerances of ![]() :
:
When method "SCS" is specified, it is called with the SCS library default tolerance of 10-3:
With default options, this problem is solved by method "SCS" with tolerance 10-6:
Use methods "CSDP" or "DSDP" for constraints that are converted to semidefinite constraints:
Solve the problem using method "CSDP":
Solve the problem using method "DSDP":
Use method "IPOPT" to obtain accurate solutions when "CSDP" and "DSDP" are not applicable:
"IPOPT" produces more accurate results than "SCS", but is typically much slower:
PerformanceGoal (1)
The default value of the option PerformanceGoal is $PerformanceGoal:
Use PerformanceGoal"Quality" to get a more accurate result:
Use PerformanceGoal"Speed" to get a result faster, but at the cost of quality:
Tolerance (2)
A smaller Tolerance setting gives a more precise result:
Compute the exact minimum value with Minimize:
Compute the error in the minimum value with different Tolerance settings:
Visualize the change in minimum value error with respect to tolerance:
A smaller Tolerance setting gives a more precise answer, but may take longer to compute:
WorkingPrecision (2)
The default working precision is MachinePrecision:
Using WorkingPrecisionInfinity will give an exact solution if possible:
WorkingPrecision other than MachinePrecision and ∞ will try to use a method with extended precision support:
Using WorkingPrecisionAutomatic will try to use the precision of the input problem:
Solve a problem with a quadratic objective using 24-digit precision:
There is currently no method that solves problems with quadratic objectives using exact arithmetic. When the requested precision is not supported, the computation uses machine numbers:
Applications (30)
Basic Modeling Transformations (11)
Maximize ![]() subject to
subject to ![]() . Solve a maximization problem by negating the objective function:
. Solve a maximization problem by negating the objective function:
Negate the primal minimum value to get the corresponding maximal value:
Minimize ![]() subject to
subject to ![]() . Since the constraint
. Since the constraint ![]() is not convex, use a semidefinite constraint to make the convexity explicit:
is not convex, use a semidefinite constraint to make the convexity explicit:
A matrix is positive semidefinite if and only if the determinants of all upper-left submatrices are non-negative:
Minimize ![]() subject to
subject to ![]() , assuming
, assuming ![]() when
when ![]() . Using the auxiliary variable
. Using the auxiliary variable ![]() , the objective is to minimize
, the objective is to minimize ![]() such that
such that ![]() :
:
A Schur complement condition says that if ![]() , a block matrix
, a block matrix ![]() iff
iff ![]() . Therefore,
. Therefore, ![]() iff
iff ![]() . Use Inactive[Plus] for constructing the constraints to avoid threading:
. Use Inactive[Plus] for constructing the constraints to avoid threading:
Minimize ![]() over an ellipse centered at
over an ellipse centered at ![]() :
:
The epigraph transformation can be used to construct a problem with a linear objective and additional variable and constraint:
In this form, the problem can be solved directly with ConicOptimization:
Minimize ![]() , where
, where ![]() is a nondecreasing function, by instead minimizing
is a nondecreasing function, by instead minimizing ![]() . The primal minimizer
. The primal minimizer ![]() will remain the same for both problems. Consider minimizing
will remain the same for both problems. Consider minimizing ![]() subject to
subject to ![]() :
:
The minimum value for ![]() can be obtained by applying
can be obtained by applying ![]() to the minimum value of
to the minimum value of ![]() :
:
ConvexOptimization will automatically do this transformation:
Find ![]() that minimizes the largest eigenvalue of a symmetric matrix that depends linearly on the decision variables
that minimizes the largest eigenvalue of a symmetric matrix that depends linearly on the decision variables ![]() ,
, ![]() . The problem can be formulated as a linear matrix inequality since
. The problem can be formulated as a linear matrix inequality since ![]() is equivalent to
is equivalent to ![]() , where
, where ![]() is the
is the ![]()
![]() eigenvalue of
eigenvalue of ![]() . Define the linear matrix function
. Define the linear matrix function ![]() :
:
A real symmetric matrix ![]() can be diagonalized with an orthogonal matrix
can be diagonalized with an orthogonal matrix ![]() so
so ![]() . Hence
. Hence ![]() iff
iff ![]() . Since any
. Since any ![]() , taking
, taking ![]() ,
, ![]() , hence
, hence ![]() iff
iff ![]() . Numerically simulate to show that these formulations are equivalent:
. Numerically simulate to show that these formulations are equivalent:
Run a Monte Carlo simulation to check the plausibility of the result:
Find ![]() that maximizes the smallest eigenvalue of a symmetric matrix
that maximizes the smallest eigenvalue of a symmetric matrix ![]() that depends linearly on the decision variables
that depends linearly on the decision variables ![]() . Define the linear matrix function
. Define the linear matrix function ![]() :
:
The problem can be formulated as linear matrix inequality, since ![]() is equivalent to
is equivalent to ![]() where
where ![]() is the
is the ![]()
![]() eigenvalue of
eigenvalue of ![]() . To maximize
. To maximize ![]() , minimize
, minimize ![]() :
:
Run a Monte Carlo simulation to check the plausibility of the result:
Find ![]() that minimizes the difference between the largest and the smallest eigenvalues of a symmetric matrix
that minimizes the difference between the largest and the smallest eigenvalues of a symmetric matrix ![]() that depends linearly on the decision variables
that depends linearly on the decision variables ![]() . Define the linear matrix function
. Define the linear matrix function ![]() :
:
The problem can be formulated as a linear matrix inequality, since ![]() is equivalent to
is equivalent to ![]() , where
, where ![]() is the
is the ![]()
![]() eigenvalue of
eigenvalue of ![]() . Solve the resulting problem:
. Solve the resulting problem:
In this case, the minimum and maximum eigenvalues coincide and the difference is 0:
Minimize the largest (by absolute value) eigenvalue of a symmetric matrix ![]() that depends linearly on the decision variables
that depends linearly on the decision variables ![]() :
:
The largest eigenvalue satisfies ![]() The largest (by absolute value) negative eigenvalue of
The largest (by absolute value) negative eigenvalue of ![]() is the largest eigenvalue of
is the largest eigenvalue of ![]() and satisfies
and satisfies ![]() :
:
Find ![]() that minimizes the largest singular value
that minimizes the largest singular value ![]() of a symmetric matrix
of a symmetric matrix ![]() that depends linearly on the decision variables
that depends linearly on the decision variables ![]() :
:
The largest singular value ![]() of
of ![]() is the square root of the largest eigenvalue of
is the square root of the largest eigenvalue of ![]() , and from a preceding example it satisfies
, and from a preceding example it satisfies ![]() , or equivalently
, or equivalently ![]() :
:
For quadratic sets ![]() , which include ellipsoids, quadratic cones and paraboloids, determine whether
, which include ellipsoids, quadratic cones and paraboloids, determine whether ![]() , where
, where ![]() are symmetric matrices,
are symmetric matrices, ![]() are vectors and
are vectors and ![]() scalars:
scalars:
Assuming that the sets ![]() are full dimensional, the S-procedure says that
are full dimensional, the S-procedure says that ![]() iff there exists some non-negative number
iff there exists some non-negative number ![]() such that
such that ![]() Visually see that there exists a non-negative
Visually see that there exists a non-negative ![]() :
:
Use 0 for an objective function since feasibility is a concern. Since λ≥0, it follows that ![]() :
:
Geometry Problems (8)
Minimize the length of the diagonal of a rectangle of area 4 such that the width plus three times the height is less than 7:
Find the minimum distance between two disks of radius 1 centered at ![]() and
and ![]() . Let
. Let ![]() be a point on disk 1. Let
be a point on disk 1. Let ![]() be a point on disk 2. The objective is to minimize
be a point on disk 2. The objective is to minimize ![]() subject to constraints
subject to constraints ![]() :
:
Visualize the positions of the two points:
The distance between the points is:
Find the half-lengths of the principal axes ![]() that maximize the volume of an ellipsoid with a surface area of at most 1:
that maximize the volume of an ellipsoid with a surface area of at most 1:
The surface area can be approximated by:
Maximize the volume area by minimizing its reciprocal:
This is the sphere. Including additional constraints on the axes lengths changes this:
Find the radius ![]() and center
and center ![]() of a minimal enclosing ball that encompasses a given region:
of a minimal enclosing ball that encompasses a given region:
Minimize the radius ![]() subject to the constraints
subject to the constraints ![]() :
:
The minimal enclosing ball can be found efficiently using BoundingRegion:
Find the analytic center of a convex polygon. The analytic center is a point that maximizes the product of distances to the constraints:
Each segment of the convex polygon can be represented as intersections of half-planes ![]() . Extract the linear inequalities:
. Extract the linear inequalities:
The objective is to maximize ![]() . Taking
. Taking ![]() and negating the objective, the transformed objective is
and negating the objective, the transformed objective is ![]() :
:
Using auxiliary variable ![]() , the transformed objective is
, the transformed objective is ![]() subject to the constraint
subject to the constraint ![]() :
:
Visualize the location of the center:
Test whether an ellipsoid is a subset of another ellipsoid of the form ![]() :
:
Using the S-procedure, it can be shown that ellipse 2 is a subset of ellipse 1 iff ![]() :
:
Check if the condition is satisfied:
Convert the ellipsoids into explicit form and confirm that ellipse 2 is within ellipse 1:
Move ellipsoid 2 such that it overlaps with ellipsoid 1:
A test now shows that the problem is infeasible, indicating that ellipsoid 2 is not a subset of ellipsoid 1:
Find the maximum-area ellipse parametrized as ![]() that can be fitted into a convex polygon:
that can be fitted into a convex polygon:
Each segment of the convex polygon can be represented as intersections of half-planes ![]() . Extract the linear inequalities:
. Extract the linear inequalities:
Applying the parametrization to the half-planes gives ![]() . The term
. The term ![]() . Thus, the constraints are
. Thus, the constraints are![]() :
:
Minimizing the area is equivalent to minimizing ![]() , which is equivalent to minimizing
, which is equivalent to minimizing ![]() :
:
Convert the parametrized ellipse into the explicit form as ![]() :
:
Find the smallest ellipsoid parametrized as ![]() that encompasses a set of points in 3D by minimizing the volume:
that encompasses a set of points in 3D by minimizing the volume:
For each point ![]() , the constraint
, the constraint ![]() must be satisfied:
must be satisfied:
Minimizing the volume is equivalent to minimizing ![]() , which is equivalent to minimizing
, which is equivalent to minimizing ![]() :
:
Convert the parametrized ellipse into the explicit form ![]() :
:
A bounding ellipsoid, not necessarily minimum volume, can also be found using BoundingRegion:
Data-Fitting Problems (4)
Minimize ![]() subject to the constraints
subject to the constraints ![]() for a given matrix a and vector b:
for a given matrix a and vector b:
Fit a cubic curve to discrete data such that the first and last points of the data lie on the curve:
Construct the matrix using DesignMatrix:
Define the constraint so that the first and last points must lie on the curve:
Find the coefficients ![]() by minimizing
by minimizing ![]() :
:
Find a fit less sensitive to outliers to nonlinear discrete data by minimizing ![]() :
:
Fit the data using the bases ![]() . The interpolating function will be
. The interpolating function will be ![]() :
:
Compare the interpolating function with the reference function:
Find an ![]() regularized fit to complex data by minimizing
regularized fit to complex data by minimizing ![]() for a complex
for a complex ![]() :
:
Construct the matrix ![]() using DesignMatrix, for the basis
using DesignMatrix, for the basis ![]() :
:
Let ![]() be the fit defined as a function of the real and imaginary components of
be the fit defined as a function of the real and imaginary components of ![]() :
:
Sum-of-Squares Representation (1)
Represent a given polynomial ![]() in terms of the sum-of-squares polynomial
in terms of the sum-of-squares polynomial ![]() :
:
The objective is to find ![]() such that
such that ![]() , where
, where ![]() is a vector of monomials:
is a vector of monomials:
Construct the symmetric matrix ![]() :
:
Find the polynomial coefficients of ![]() and
and ![]() and make sure they are equal:
and make sure they are equal:
The quadratic term ![]() , where
, where ![]() is a lower-triangular matrix obtained from the Cholesky decomposition of
is a lower-triangular matrix obtained from the Cholesky decomposition of ![]() :
:
Compare the sum-of-squares polynomial to the given polynomial:
Classification Problems (3)
Find a line ![]() that separates two groups of points
that separates two groups of points ![]() and
and ![]() :
:
For separation, set 1 must satisfy ![]() and set 2 must satisfy
and set 2 must satisfy ![]() :
:
The objective is to minimize ![]() , which gives twice the thickness between
, which gives twice the thickness between ![]() and
and ![]() :
:
Find a quadratic polynomial that separates two groups of 3D points ![]() and
and ![]() :
:
Construct the quadratic polynomial data matrices for the two sets using DesignMatrix:
For separation, set 1 must satisfy ![]() and set 2 must satisfy
and set 2 must satisfy ![]() :
:
Find the separating polynomial by minimizing ![]() :
:
The polynomial separating the two groups of points is:
Plot the polynomial separating the two datasets:
Separate a given set of points ![]() into different groups. This is done by finding the centers
into different groups. This is done by finding the centers ![]() for each group by minimizing
for each group by minimizing ![]() , where
, where ![]() is a given local kernel and
is a given local kernel and ![]() is a given penalty parameter:
is a given penalty parameter:
The kernel ![]() is a
is a ![]() -nearest neighbor (
-nearest neighbor (![]() ) function such that
) function such that ![]() , else
, else ![]() . For this problem,
. For this problem, ![]() nearest neighbors are selected:
nearest neighbors are selected:
For each data point, there exists a corresponding center. Data belonging to the same group will have the same center value:
Facility Location Problems (1)
Find the positions of various cell towers ![]() and the range
and the range ![]() needed to serve clients located at
needed to serve clients located at ![]() :
:
Each cell tower consumes power proportional to its range, which is given by ![]() . The objective is to minimize the power consumption:
. The objective is to minimize the power consumption:
Let ![]() be a decision variable indicating that
be a decision variable indicating that ![]() if client
if client ![]() is covered by cell tower
is covered by cell tower ![]() :
:
Each cell tower must be located such that its range covers some of the clients:
Each cell tower can cover multiple clients:
Each cell tower has a minimum and maximum coverage:
Find the cell tower positions and their ranges:
Extract cell tower position and range:
Visualize the positions and ranges of the towers with respect to client locations:
Portfolio Optimization (1)
Find the distribution of capital ![]() to invest in six stocks to maximize return while minimizing risk:
to invest in six stocks to maximize return while minimizing risk:
The return is given by ![]() , where
, where ![]() is a vector of expected return value of each individual stock:
is a vector of expected return value of each individual stock:
The risk is given by ![]() ;
; ![]() is a risk-aversion parameter and
is a risk-aversion parameter and ![]() :
:
The objective is to maximize return while minimizing risk for a specified risk-aversion parameter:
The effect on market prices of stocks due to the buying and selling of stocks is modeled by ![]() , which is modeled by a power cone using the epigraph transformation:
, which is modeled by a power cone using the epigraph transformation:
The weights ![]() must all be greater than 0 and the weights plus market impact costs must add to 1:
must all be greater than 0 and the weights plus market impact costs must add to 1:
Compute the returns and corresponding risk for a range of risk-aversion parameters:
The optimal ![]() over a range of
over a range of ![]() gives an upper-bound envelope on the tradeoff between return and risk:
gives an upper-bound envelope on the tradeoff between return and risk:
Compute the weights for a specified number of risk-aversion parameters:
By accounting for the market costs, a diversified portfolio can be obtained for low risk aversion, but when the risk aversion is high, the market impact cost dominates, due to purchasing a less diversified stock:
Image Processing (1)
Tech Notes
Related Guides
History
Text
Wolfram Research (2020), ConvexOptimization, Wolfram Language function, https://reference.wolfram.com/language/ref/ConvexOptimization.html.
CMS
Wolfram Language. 2020. "ConvexOptimization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ConvexOptimization.html.
APA
Wolfram Language. (2020). ConvexOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConvexOptimization.html
BibTeX
@misc{reference.wolfram_2025_convexoptimization, author="Wolfram Research", title="{ConvexOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ConvexOptimization.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_convexoptimization, organization={Wolfram Research}, title={ConvexOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/ConvexOptimization.html}, note=[Accessed: 09-January-2026]}