RobustConvexOptimization
RobustConvexOptimization[f,ForAll[pars,pcons,vcons],vars]
求能给出 f 的最小值的 vars 的值,其中,对于满足参数约束条件 pcons 的参数 pars 所有可能的值,vars 满足约束条件 vcons.
RobustConvexOptimization[…,"prop"]
指定应返回的解的属性 "prop".
更多信息和选项




- 稳健优化亦称为最坏情况的优化.
- 当在不确定性由含有参数约束条件的参数表示的情况下求解优化问题时,通常会使用稳健优化.
- 在针对所有可能的参数值能实现的最优解的意义上,稳健优化给出了最保守的解.
- 稳健优化给出可求解以下问题的稳健的最小值点 (minimizer)
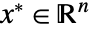 :
: -
最小化 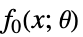
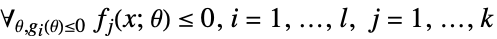
其中 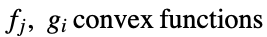
- 对于参数集中的所有
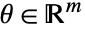 ,稳健的最小值点
,稳健的最小值点 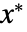 满足
满足 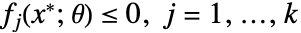 .
. - 对于参数集中的所有
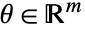 ,稳健的最小值
,稳健的最小值 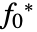 满足
满足 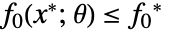 .
. - pcons 或 vcons 可包括线性等式约束条件
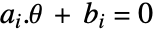 或
或 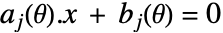 .
. - 也可以使用 RobustConvexOptimization[f,cons,vars,pars]. 约束条件 cons 被自动分为纯参数约束条件
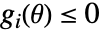 和可能依赖于参数的变量约束条件
和可能依赖于参数的变量约束条件 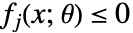 . 这种形式与 ParametricConvexOptimization 兼容.
. 这种形式与 ParametricConvexOptimization 兼容. - 如果稳健优化问题能转化为可以通过凸优化求解或近似的形式,则认为该问题是可以处理的. 可处理性取决于变量约束条件
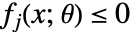 的类型和参数约束条件
的类型和参数约束条件 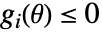 的类型的组合.
的类型的组合. - 下面的变量约束条件和参数约束条件的组合被视为可处理的情况:
-
变量约束条件 参数约束条件 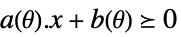
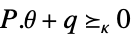
![TemplateBox[{{{a, ., x}, +, b}}, Norm]<=c(theta).x+d(theta) TemplateBox[{{{a, ., x}, +, b}}, Norm]<=c(theta).x+d(theta)](Files/RobustConvexOptimization.zh/19.png)
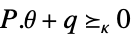
![TemplateBox[{{{{a, (, theta, )}, ., x}, +, {b, (, theta, )}}}, Norm]<=c.x+d TemplateBox[{{{{a, (, theta, )}, ., x}, +, {b, (, theta, )}}}, Norm]<=c.x+d](Files/RobustConvexOptimization.zh/21.png)
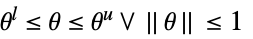
![TemplateBox[{{{{a, (, {theta, _, l}, )}, ., x}, +, {b, (, {theta, _, l}, )}}}, Norm]<=c(theta_r).x+d(theta_r) TemplateBox[{{{{a, (, {theta, _, l}, )}, ., x}, +, {b, (, {theta, _, l}, )}}}, Norm]<=c(theta_r).x+d(theta_r)](Files/RobustConvexOptimization.zh/23.png)
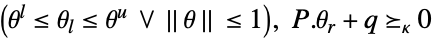
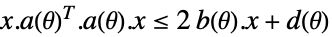
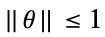
![a_0(theta)+a_1(theta) x_1+...+a_k(theta) x_k>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_0(theta)+a_1(theta) x_1+...+a_k(theta) x_k>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/RobustConvexOptimization.zh/27.png)
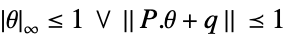
- 通常,变量约束条件
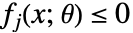 被转换为形式为
被转换为形式为 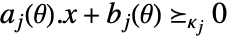 的锥约束条件,其中
的锥约束条件,其中 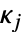 是 "NonNegativeCone" 、"NormCone" 或 "SemidefiniteCone" 之一,
是 "NonNegativeCone" 、"NormCone" 或 "SemidefiniteCone" 之一,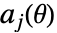 和
和 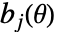 对参数的依赖关系应是仿射的.
对参数的依赖关系应是仿射的. - 当目标函数
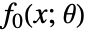 依赖于参数或是非线性的,将引入另一个变量
依赖于参数或是非线性的,将引入另一个变量 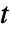 ,且通过上镜图变换将问题转化成目标函数
,且通过上镜图变换将问题转化成目标函数 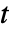 具有额外的约束条件
具有额外的约束条件 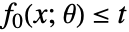 .
. - 变量和参数指定 vars 和 pars 应为列表,其中的元素按以下形式给出变量和参数:
-
v 名为 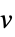 的维度由推断而得的变量或标量参数
的维度由推断而得的变量或标量参数v∈Reals 实标量变量 v∈Integers 整数标量变量 v∈Complexes 复标量变量 v∈ℛ 限制于几何区域 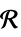 的向量变量
的向量变量v∈Vectors[n,dom] 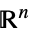 、
、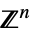 或
或 ![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/RobustConvexOptimization.zh/42.png) 中的向量变量
中的向量变量v∈Matrices[{m,n},dom] 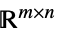 、
、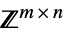 或
或 ![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/RobustConvexOptimization.zh/45.png) 中的矩阵变量
中的矩阵变量 - 可能的解的属性 "prop" 包括:
-
"PrimalMinimizer" 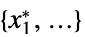
最小化 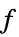 的变量值列表
的变量值列表"PrimalMinimizerRules" 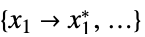
最小化 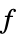 的变量 vars={v1,…} 的值
的变量 vars={v1,…} 的值"PrimalMinimizerVector" 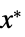
最小化 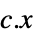 的向量
的向量"PrimalMinimumValue" 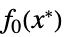
最小值 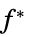
{"prop1","prop2",…} 几个解的属性 - 可给出以下选项:
-
MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 Tolerance Automatic 内部比较采用的容差 - 选项 Methodmethod 可用来指定使用的方法. 可用的方法包括:
-
Automatic 自动选择方法 "CuttingSet" 使用割集法 "PolyhedralApproximation" 用一组线性约束条件近似 "NormCone" 约束条件 "SCS" SCS (splitting conic solver) 库 "CSDP" CSDP (COIN semidefinite programming) 库 "DSDP" DSDP (semidefinite programming) 库 - 使用割集法可以近似求解一些难以解决的稳健优化问题.
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (29)
基本用法 (15)
对于所有位于区间 ![]() 的
的 ![]() ,求受约束条件
,求受约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
不给出 ForAll,使用其他语法:
下面的语法可直接被用在 ParametricConvexOptimization 中,用来尝试具体的 ![]() 的值:
的值:
用 VectorLessEqual 一次性表示几个 LessEqual 不等式约束条件:
用 VectorGreaterEqual 一次性表示几个 GreaterEqual 不等式约束条件:
用 Indexed 指代向量变量的分量,如 ![]() :
:
需要的情况下用 Vectors[n,Reals] 指定向量变量的维度:
用 NonNegativeReals (![]() ) 指定非负约束条件:
) 指定非负约束条件:
用 NonPositiveReals (![]() ) 指定非正约束条件:
) 指定非正约束条件:
用 Interval 指定界限:
线性变量约束条件 (5)
对于位于区间 [0,2] 中的所有 ![]() ,求受
,求受 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
对于位于 [0,2] 中的所有 ![]() ,数学上来讲,约束条件
,数学上来讲,约束条件 ![]() 意味着
意味着 ![]() . 因此,问题等价于:
. 因此,问题等价于:
对于所有限制在区间中的 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点和 ![]() 取极端值的情况下的变量约束条件集. 对于参数
取极端值的情况下的变量约束条件集. 对于参数 ![]() 所有可能的值而言,可行的
所有可能的值而言,可行的 ![]() 集合(显示为绿色)为参数可行区域的交集:
集合(显示为绿色)为参数可行区域的交集:
对于所有限制在区间中的 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点、参数 ![]() 的极端值的变量约束条件集和可行区域(显示为绿色):
的极端值的变量约束条件集和可行区域(显示为绿色):
可视化最小值点、参数 ![]() 取极端值时的变量约束条件集和可行区域(显示为绿色):
取极端值时的变量约束条件集和可行区域(显示为绿色):
NormCone 变量约束条件 (7)
对于满足 ![]() 的所有
的所有 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点和 ![]() 取极端值时的变量约束条件集. 对于参数
取极端值时的变量约束条件集. 对于参数 ![]() 所有可能的值而言,可行的
所有可能的值而言,可行的 ![]() 集合为所有可行区域的交集(显示为绿色):
集合为所有可行区域的交集(显示为绿色):
对于满足 ![]() 的所有
的所有 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点、参数 ![]() 取极端值时的变量约束条件集和可行区域(显示为绿色):
取极端值时的变量约束条件集和可行区域(显示为绿色):
对于满足 ![]() 的所有
的所有 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点、![]() 取极端值时的变量约束条件集和可行区域(显示为绿色):
取极端值时的变量约束条件集和可行区域(显示为绿色):
对于满足 ![]() 的所有
的所有 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点、![]() 取极端值时的变量约束条件集和可行区域(显示为绿色):
取极端值时的变量约束条件集和可行区域(显示为绿色):
对于满足 ![]() 的所有
的所有 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点::
的稳健最小值点::
对于满足 ![]() 的所有
的所有 ![]() ,求受变量约束条件
,求受变量约束条件 ![]() 限制的
限制的 ![]() 的稳健最小值点:
的稳健最小值点:
可视化最小值点、![]() 取极端值时的变量约束条件集和可行区域(显示为绿色):
取极端值时的变量约束条件集和可行区域(显示为绿色):
选项 (3)
应用 (14)
几何问题 (2)
数据拟合问题 (3)
目标是使输入和输出之间的误差最小,该误差取决于区间的不确定性 ![]() :
:
显示拟合模型的包络,其中有稳健拟合(黑色)、简单拟合(绿色)和数据:
用 DesignMatrix 构建输入矩阵:
目标是使输入和输出之间的误差最小,该误差取决于区间的不确定性 ![]() :
:
生产制造问题 (3)
给定从两种不同原料 ![]() 中提取活性剂的不确定性,求公司生产两种药物
中提取活性剂的不确定性,求公司生产两种药物 ![]() 的最佳组合,以使利润最大化. 每单位药物带来的收入为:
的最佳组合,以使利润最大化. 每单位药物带来的收入为:
生产这两种药物需要 90 到 100 个小时的人力. 该公司只有 2000 个小时的可用人力:
生产这两种药物需要 40 到 50 个小时的设备时间. 该公司只有 800 个小时的可用设备时间:
生产这两种药物的运营成本分别为 700 和 800. 每公斤的原料成本分别为 100 和 199.9:
从这两种原料中提取的活性剂的量分别为 ![]() g/kg 和
g/kg 和 ![]() g/kg. 两种药物分布需要 0.5 g/unit 和 0.6 g/unit 的活性剂:
g/kg. 两种药物分布需要 0.5 g/unit 和 0.6 g/unit 的活性剂:
要想看到使用稳健解的优势,使用原材料和活性剂的不确定性作为参数来生成参数化函数:
如果使用标称结果购买原料,即 ![]() ,则利润可能会下降 21%,具体取决于可以从原料中提取出多少活性剂:
,则利润可能会下降 21%,具体取决于可以从原料中提取出多少活性剂:
在生产投入存在一定不确定性的情况下,求可以使公司利润最大化的产品组合. 该公司生产三种产品. 在理想条件下,每个单位带来的收入、成本和最大产能由下式给出:
每个产品要使用四台机器制造. 机器在每种产品上花费的时间为:
考虑到机器的停机时间,每个产品的产能可能会降低 5 个单位:
每台机器每周最多可以运行 2400 分钟. 如果机器无法运行,则最多需要 120 分钟才能使其恢复工作状态:
修理四台机器中的任何一台的成本会使每种产品的成本每单位增加 $5:
最差的情况则对应于 RobustConvexOptimization 的结果:
找出可以使公司利润最大化的产品组合,公司制造三种产品 ![]() ,三种产品受价格和供应波动的影响:
,三种产品受价格和供应波动的影响:
工厂只生产 100 天. 理想情况下,分别需要 2、4 或 5 天来制造每种产品,但由于意外的延迟,制造时间可能会增加一天:
每种产品都包含金和锡. 可用的金和锡的总量分别为 ![]() 和
和 ![]() 个单位:
个单位:
由于相对较高的设置成本,可能希望根本不生产某些产品. 令 ![]() 为决策变量,如果生产产品
为决策变量,如果生产产品 ![]() ,
,![]() ,否则
,否则 ![]() . 限制
. 限制 ![]() 确保如果
确保如果 ![]() 为 0,则
为 0,则 ![]() 也为 0,不必对
也为 0,不必对 ![]() 作出比其他限制条件更严格的限制:
作出比其他限制条件更严格的限制:
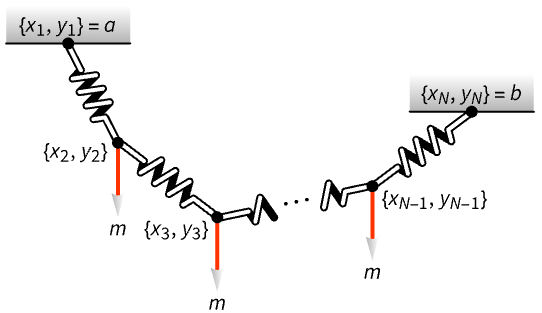
结构优化问题 (1)
投资组合优化 (2)
选址问题 (1)
分类问题 (2)
对于此分隔问题,第 1 组必须满足 ![]() ,第 2 组必须满足
,第 2 组必须满足 ![]() :
:
可视化不确定性增加的集合,显示这两个集合有一些不确定性方框重叠的点:
求分隔两组 3D 点 ![]() 和
和 ![]() 的二次多项式,其中
的二次多项式,其中 ![]() 为区间不确定性:
为区间不确定性:
用 DesignMatrix 构建两组点的二次多项式数据矩阵:
文本
Wolfram Research (2020),RobustConvexOptimization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RobustConvexOptimization.html.
CMS
Wolfram 语言. 2020. "RobustConvexOptimization." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RobustConvexOptimization.html.
APA
Wolfram 语言. (2020). RobustConvexOptimization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RobustConvexOptimization.html 年