ShenCastanMatrix

ShenCastanMatrix[r]

半径 r の指数カーネルに対応する行列を与える．

ShenCastanMatrix[{r,σ}]

半径 r で台の範囲が σ で指定される指数カーネルに対応する行列を与える．

ShenCastanMatrix[r,{n1,n2}]

行については指数関数の n1次導関数から，列については指数関数の n2次導関数から形成される行列を与える．

ShenCastanMatrix[r,{{n11,n12},{n21,n22},…}]

ni1次と ni2次の導関数の合計から形成される行列を与える．

ShenCastanMatrix[{{r1,r2,…},σ},…]

第 i 次指標方向で半径 riの指数カーネルに対応する配列を与える．

詳細とオプション

  • ShenCastanMatrix[{r,σ}]は中心からの x 個の指標の位置で exp(-TemplateBox[{x}, Abs]/b)に比例する値を与える．ただし，b は σ に比例し，σ=r/2の値は指数関数の下で総面積のおよそ95％を与える．
  • ShenCastanMatrix[r]は 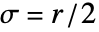を使う．
  • デフォルトで，ShenCastanMatrix[r]の要素の合計は1になる．
  • ShenCastanMatrix[…,{n1,n2}]は導関数を有限差分として構築する．
  • ShenCastanMatrix[{Automatic,σ,f},…]は各方向の指数関数の離散積分の少なくとも割合 f を含むにちょうど足りるだけの大きさを持つ行列を構築する．
  • 任意の r，σ，f を，異なる方向について異なる値を指定するリストにすることができる．
  • 整数 r について，ShenCastanMatrix[r,…]は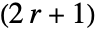×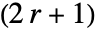行列を与える．
  • 非整数 r では，r の値は事実上四捨五入して整数にされる．
  • 指定可能なオプション
  • Standardized True切断を説明するために行列を再スケールしてシフトするかどうか
    WorkingPrecision Automatic行列要素を計算する精度
  • Standardized->Trueのとき，ShenCastanMatrix[r]の要素の合計は1になる．しかし，最低でも1つの非零の niを含むShenCastanMatrix[r,{n1,n2,…}]の要素の合計は0であり，各方向に原点から niのベキまでの距離に 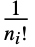を掛けたもので重みの付いた要素の合計は1になる．

例題

すべて開くすべて閉じる

例  (3)

半径20の指数行列：

指数行列のMatrixPlot：

1D指数ベクトル：

スコープ  (3)

指数関数の導関数  (3)

1D指数ベクトルの一次導関数：

垂直次元での指数行列の一次導関数：

3D指数配列の一次導関数：

オプション  (5)

Standardized  (3)

正規化された指数行列：

正規化されていない指数行列：

正規化されていない行列の合計は，その大きさと台の範囲の比が大きくなるにつれて1に近付く：

正規化された指数導関数ベクトルの平均は0である：

正規化されていない指数導関数ベクトルの平均：

シフトされた指数導関数もまた正規化されている：

正規化されていない指数導関数：

WorkingPrecision  (2)

厳密記号指数行列を生成する：

機械精度の指数行列：

機械精度の指数ベクトル：

高精度の指数ベクトル：

特性と関係  (1)

導関数は有限差分を使って計算される：

Wolfram Research (2012), ShenCastanMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/ShenCastanMatrix.html （2015年に更新）.

テキスト

Wolfram Research (2012), ShenCastanMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/ShenCastanMatrix.html （2015年に更新）.

CMS

Wolfram Language. 2012. "ShenCastanMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/ShenCastanMatrix.html.

APA

Wolfram Language. (2012). ShenCastanMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ShenCastanMatrix.html

BibTeX

@misc{reference.wolfram_2024_shencastanmatrix, author="Wolfram Research", title="{ShenCastanMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/ShenCastanMatrix.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_shencastanmatrix, organization={Wolfram Research}, title={ShenCastanMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/ShenCastanMatrix.html}, note=[Accessed: 25-November-2024 ]}