GaussianFilter

GaussianFilter[data,r]

filters data by convolving with a Gaussian kernel of radius r.

GaussianFilter[data,r,{n1,n2,…}]

convolves data with a kernel formed from the ni^(th) derivatives of the discrete Gaussian.

GaussianFilter[data,{r,σ},…]

uses a Gaussian kernel with radius r and standard deviation σ.

GaussianFilter[data,{{r1,r2,…},…}]

uses radius ri at level i in data.

Details and Options

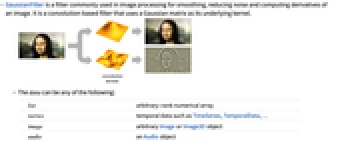
  • GaussianFilter is a filter commonly used in image processing for smoothing, reducing noise and computing derivatives of an image. It is a convolution-based filter that uses a Gaussian matrix as its underlying kernel.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries, TemporalData, …
    imagearbitrary Image or Image3D object
    audioan Audio object
  • GaussianFilter[data,r] uses standard deviation .
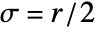  • GaussianFilter[data,…] by default gives an array, audio or image of the same dimensions as data.
  • The following options can be specified:
  • Method "Bessel"how to determine elements of the Gaussian matrix
    Padding "Fixed"padding method
    Standardized Truewhether to rescale and shift the Gaussian matrix to account for truncation
    WorkingPrecision Automaticthe precision to use
  • Possible settings for the Method option are "Bessel" and "Gaussian".
  • With a setting Padding->None, GaussianFilter[data,…] normally returns an array, audio or image smaller than data. »

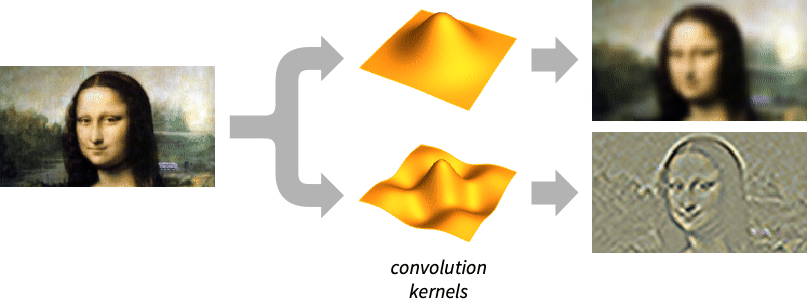
Background & Context

  • GaussianFilter is a filter commonly used in image processing for smoothing, reducing noise, and computing derivatives of an image. It is a convolution-based filter that uses a Gaussian matrix as its underlying kernel.
  • Gaussian filtering is linear, meaning it replaces each pixel by a linear combination of its neighbors (in this case with weights specified by a Gaussian matrix). It is also local, meaning it produces output pixel values based only upon the pixel values in its neighborhood as determined by the convolution kernel.
  • Gaussian filtering is not edge preserving, so other filters such as BilateralFilter and MeanShiftFilter may be more appropriate in applications where edges must be preserved.
  • Applying GaussianFilter is equivalent to using ImageConvolve with a GaussianMatrix kernel. MeanFilter is a similar smoothing filter.

Examples

open allclose all

Basic Examples  (3)

Gaussian filter of a list:

Gaussian blurring of a color image:

First-order Gaussian derivative of an image:

Scope  (10)

Data  (6)

Gaussian filtering of a numeric vector:

Gaussian derivative of a numeric vector:

Gaussian blurring of a numeric matrix:

Filter a TimeSeries:

Filter an Audio signal:

Smooth a grayscale image:

Apply Gaussian first derivatives to both dimensions of the image:

Gaussian smoothing of a 3D image:

Third-order Gaussian derivative of the image:

Parameters  (4)

Gaussian smoothing of a step sequence:

Use a custom standard deviation:

Compare the two results:

Show the first, second, and third Gaussian derivatives of the step sequence:

Vertical-only Gaussian blurring:

Vertical Gaussian derivative:

Horizontal Gaussian derivative:

Gaussian smoothing of a 3D image in the vertical direction only:

Filtering of the horizontal planes only:

Gaussian derivative of a 3D image in the vertical direction only:

Filtering of the horizontal planes only:

Options  (10)

Method  (1)

By default, method "Bessel" is used to obtain the filter coefficients:

Use method "Gaussian":

Padding  (4)

Smoothing with GaussianFilter using different padding methods:

By default, a "Fixed" padding is used:

Specify a custom padding:

Padding->None normally returns an image smaller than the input image:

Standardized  (1)

The default setting is True:

Use Standardized->False:

WorkingPrecision  (4)

MachinePrecision is by default used with integer arrays:

Perform exact computation instead:

With real arrays, by default the precision of the input is used:

Specify the precision to use:

With symbolic arrays, exact computation is used:

WorkingPrecision is ignored when filtering images:

An image of a real type is always returned:

Applications  (6)

Smoothing & Sharpening  (3)

Use GaussianFilter to smooth a time series and identify the trend:

Compute an unsharp mask:

Add the unsharp mask to the original image:

Boost the unsharp masking effect:

Remove Gaussian color noise from an image:

Convert the image to LABColor space:

Apply median filtering to the channel and Gaussian filtering to the color channels and :

Derivatives  (3)

Use GaussianFilter to denoise an audio signal:

Compute the image gradient:

Compute the Laplacian of an image:

Properties & Relations  (5)

Impulse responses of Gaussian smoothing filter for selected radii:

Gaussian derivative impulse responses in 2D:

Gaussian filtering returns an image of a real type:

Perform Gaussian filtering using ImageConvolve:

GaussianFilter is a linear filter:

Wolfram Research (2008), GaussianFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianFilter.html (updated 2016).

Text

Wolfram Research (2008), GaussianFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GaussianFilter.html (updated 2016).

CMS

Wolfram Language. 2008. "GaussianFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GaussianFilter.html.

APA

Wolfram Language. (2008). GaussianFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianFilter.html

BibTeX

@misc{reference.wolfram_2024_gaussianfilter, author="Wolfram Research", title="{GaussianFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianFilter.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gaussianfilter, organization={Wolfram Research}, title={GaussianFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/GaussianFilter.html}, note=[Accessed: 24-November-2024 ]}