gives a matrix that corresponds to an exponential kernel of radius r.
ShenCastanMatrix[{r,σ}]
gives a matrix corresponding to an exponential kernel with radius r and region of support specified by σ.
ShenCastanMatrix[r,{n1,n2}]
gives a matrix formed from the n1![]() derivative of the exponential with respect to rows and the n2
derivative of the exponential with respect to rows and the n2![]() derivative with respect to columns.
derivative with respect to columns.
ShenCastanMatrix[r,{{n11,n12},{n21,n22},…}]
gives a matrix formed from the sums of the ni1 and ni2 derivatives.
ShenCastanMatrix[{{r1,r2,…},σ},…]
gives an array corresponding to an exponential kernel with radius ri in the i![]() index direction.
index direction.


ShenCastanMatrix
gives a matrix that corresponds to an exponential kernel of radius r.
ShenCastanMatrix[{r,σ}]
gives a matrix corresponding to an exponential kernel with radius r and region of support specified by σ.
ShenCastanMatrix[r,{n1,n2}]
gives a matrix formed from the n1![]() derivative of the exponential with respect to rows and the n2
derivative of the exponential with respect to rows and the n2![]() derivative with respect to columns.
derivative with respect to columns.
ShenCastanMatrix[r,{{n11,n12},{n21,n22},…}]
gives a matrix formed from the sums of the ni1 and ni2 derivatives.
ShenCastanMatrix[{{r1,r2,…},σ},…]
gives an array corresponding to an exponential kernel with radius ri in the i![]() index direction.
index direction.
Details and Options

- ShenCastanMatrix[{r,σ}] gives values proportional to
![exp(-TemplateBox[{x}, Abs]/b) exp(-TemplateBox[{x}, Abs]/b)](Files/ShenCastanMatrix.en/4.png) at x index positions from the center, where b is proportional to σ, so that a value of σ=r/2 gives approximately 95% of the total area under the exponential.
at x index positions from the center, where b is proportional to σ, so that a value of σ=r/2 gives approximately 95% of the total area under the exponential. - ShenCastanMatrix[r] uses
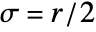 .
. - By default, the elements of ShenCastanMatrix[r] sum to 1.
- ShenCastanMatrix[…,{n1,n2}] constructs derivatives as finite differences.
- ShenCastanMatrix[{Automatic,σ,f},…] constructs a matrix just large enough to include at least a fraction f of the discrete integral of an exponential in each direction.
- Any of the r, σ, and f can be lists, specifying different values for different directions.
- For integer r, ShenCastanMatrix[r,…] yields a
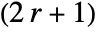 ×
×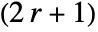 matrix.
matrix. - For noninteger r, the value of r is effectively rounded to an integer.
- The following options can be specified:
-
Standardized True whether to rescale and shift the matrix to account for truncation WorkingPrecision Automatic the precision with which to compute matrix elements - With Standardized->True, the elements of ShenCastanMatrix[r] will sum to 1. However, the elements of ShenCastanMatrix[r,{n1,n2,…}] with at least one nonzero ni will sum to 0, and the sum of the elements, weighted in each direction by
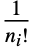 times the distance from the origin to the power of ni, will be 1.
times the distance from the origin to the power of ni, will be 1.
Examples
open all close allBasic Examples (3)
Scope (3)
Options (5)
Standardized (3)
A normalized exponential matrix:
An unnormalized exponential matrix:
The total of the unnormalized matrix approaches 1 as the ratio of its size to its region of support increases:
Normalized exponential derivative vector will have a mean of 0:
Mean of an unnormalized exponential derivative vector:
Related Guides
Text
Wolfram Research (2012), ShenCastanMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/ShenCastanMatrix.html (updated 2015).
CMS
Wolfram Language. 2012. "ShenCastanMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/ShenCastanMatrix.html.
APA
Wolfram Language. (2012). ShenCastanMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ShenCastanMatrix.html
BibTeX
@misc{reference.wolfram_2025_shencastanmatrix, author="Wolfram Research", title="{ShenCastanMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/ShenCastanMatrix.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_shencastanmatrix, organization={Wolfram Research}, title={ShenCastanMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/ShenCastanMatrix.html}, note=[Accessed: 05-February-2026]}