gives a complete maximum-length sequence for a size n linear-feedback shift register.
ShiftRegisterSequence[{n,{tap1,tap2,…}}]
gives the complete sequence for a linear-feedback shift register with size n and taps at positions tapi.
ShiftRegisterSequence[poly]
gives the sequence for a linear-feedback shift register with feedback polynomial poly.
ShiftRegisterSequence[{n,{tap1,tap2,…},f}]
gives the sequence for a shift register with feedback function f.
ShiftRegisterSequence[spec,s]
gives the first s elements of the shift register sequence.
ShiftRegisterSequence[spec,init,s]
gives the shift register sequence starting from state init.


ShiftRegisterSequence
gives a complete maximum-length sequence for a size n linear-feedback shift register.
ShiftRegisterSequence[{n,{tap1,tap2,…}}]
gives the complete sequence for a linear-feedback shift register with size n and taps at positions tapi.
ShiftRegisterSequence[poly]
gives the sequence for a linear-feedback shift register with feedback polynomial poly.
ShiftRegisterSequence[{n,{tap1,tap2,…},f}]
gives the sequence for a shift register with feedback function f.
ShiftRegisterSequence[spec,s]
gives the first s elements of the shift register sequence.
ShiftRegisterSequence[spec,init,s]
gives the shift register sequence starting from state init.
Details and Options


- ShiftRegisterSequence[n] uses a particular linear-feedback shift register of size n that gives a maximum-length sequence. When possible, a shift register with three taps is used (corresponding to a trinomial). In general, the shift register used is the one whose specification is lexically smallest.
- ShiftRegisterSequence[{n,{tap1,tap2,…}}] starts from the initial state {1,0,0,0,…}, then at each step first takes the sum mod 2 of the values at the positions tapi, then shifts all values to the left, placing the sum on the right and using this as an element of the output.
- In ShiftRegisterSequence[{n,{tap1,tap2,…},f}], the result at each step is obtained by applying f to the list of values from the position tapi.
- The default for f is effectively Mod[Total[#],2]&.
- ShiftRegisterSequence[{n,taps}] gives the same complete sequence as ShiftRegisterSequence[Total[x^(taps-1)]+x^n], though the sequence may start from a different point.
- In ShiftRegisterSequence[poly,init,s], init can be either a list of values of length n or a polynomial whose coefficients correspond to these values.
- ShiftRegisterSequence[spec,init,All] gives the complete sequence of length
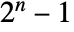 .
. - ShiftRegisterSequence[spec,All] is equivalent to ShiftRegisterSequence[spec].
- ShiftRegisterSequence has the following options:
-
Method Automatic the shift register updating method to use Modulus 2 the modulus to assume - ShiftRegisterSequence[n,Modulus->p] gives a maximum-length sequence with elements from 0 to
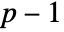 .
. - Possible settings for the Method option include:
-
"Fibonacci" use conventions suitable for explicit taps "Galois" use conventions suitable for polynomials Automatic use Fibonacci for explicit taps and Galois for polynomials - Different settings for the Method option affect the initial conditions for a maximum-length sequence but do not affect the overall sequence of states it contains.
Examples
open all close allBasic Examples (3)
Generate a maximal-length shift register sequence for a register of size 6:
Generate the sequence from a shift register with taps 6, 2, 1:
Use a shift register with the nonlinear feedback function BitOr:
Scope (4)
Properties & Relations (2)
When the sequence has maximal length, the polynomial specification corresponds to the tap specification after a rotation:
The nonlinear feedback function Total gives the same sequence as the default:
Related Guides
History
Text
Wolfram Research (2016), ShiftRegisterSequence, Wolfram Language function, https://reference.wolfram.com/language/ref/ShiftRegisterSequence.html.
CMS
Wolfram Language. 2016. "ShiftRegisterSequence." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ShiftRegisterSequence.html.
APA
Wolfram Language. (2016). ShiftRegisterSequence. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ShiftRegisterSequence.html
BibTeX
@misc{reference.wolfram_2025_shiftregistersequence, author="Wolfram Research", title="{ShiftRegisterSequence}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ShiftRegisterSequence.html}", note=[Accessed: 21-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_shiftregistersequence, organization={Wolfram Research}, title={ShiftRegisterSequence}, year={2016}, url={https://reference.wolfram.com/language/ref/ShiftRegisterSequence.html}, note=[Accessed: 21-December-2025]}