SignedRankTest

SignedRankTest[data]

data の中央値が0かどうかの検定を行う．

SignedRankTest[{data1,data2}]

data1-data2の中央値が0かどうかの検定を行う．

SignedRankTest[dspec,μ0]

μ0について位置測定の検定を行う．

SignedRankTest[dspec,μ0,"property"]

"property"の値を返す．

詳細とオプション

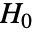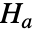  • SignedRankTestは，帰無仮説 と対立仮説 で検定を行う．
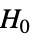
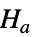
  • data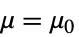
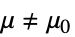
    {data1,data2}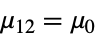
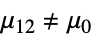
  • ただし，μ は data の母集団中央値，μ12は2つのデータ集合のペアになった差分 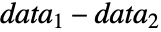の中央値である．
  • デフォルトで，確率値つまり 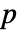値が返される．
  • 小さい 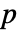値は 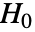が真である可能性が低いことを示唆している．
  • dspec 中のデータは一変量{x1,x2,…}でも多変量{{x1,y1,…},{x2,y2,…},…}でもよい．
  • 2つのサンプルを与える場合，両者は同じ長さでなければならない．
  • 引数 μ0は実数あるいはデータの次元と同じ長さの実ベクトルでよい．
  • SignedRankTestは一変量の場合はデータが中央値について対称であり，多変量の場合はデータが中央値について楕円対称であると仮定する．ゆえに，SignedRankTestは平均検定でもある．
  • SignedRankTest[dspec,μ0,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる．
  • SignedRankTest[dspec,μ0,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定で使用される自由度
    "PValue" 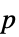値のリスト
    "PValueTable" 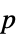値のフォーマットされた表
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 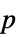値のペアのリスト
    "TestDataTable"検定統計と 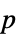値のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • SignedRankTestはSignTestより強力な選択肢である．
  • 一変量のサンプルについては，ペアになったサンプルの中央値についてSignedRankTestはウィルコクソン(Wilcoxon)の符号順位検定を行う．置換に基づいた 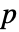値にはタイの修正が行われる．デフォルトで，検定統計は連続性について修正され，漸近的な結果が返される．
  • 多変量のサンプルについては，SignedRankTestは標準化された空間的符号順位を用いて，ペアのサンプルについてアフィン不変量検定を行う．検定統計はChiSquareDistribution[dim]に従うと仮定される．ただし，dim はデータの次元である．
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    MaxIterations Automatic多変量中央値検定のための最大反復回数
    Method Automatic 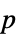値を計算するメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て
    VerifyTestAssumptions Automaticどの仮定を検証するか
  • SignedRankTestでは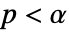， のときにのみ 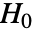が棄却されるような切捨て 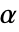が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 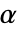の値はSignificanceLevelオプションで制御される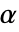． の値は対称性の検定を含む仮定の診断検定にも使われる．デフォルトで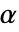， は0.05に設定されている．
  • SignedRankTestにおけるVerifyTestAssumptionsの名前付き設定
  • "Symmetry"すべてのデータが対称であることを証明する

例題

すべて開くすべて閉じる

例  (4)

母集団の中央値が0かどうかの検定を行う：

ペアになったデータと特定の値の中央値の差分を比べる：

検定結果を表にする：

多変量母集団の空間的中央値がなんらかの値かどうかの検定を行う：

検定統計を計算する：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作る：

使用可能な特性のリスト：

1つの特性または特性のリストを抽出する：

スコープ  (13)

検定  (10)

対 を検定する：

中央値が μ0に近い場合， 値は通常大きい：

位置が μ0から離れている場合， 値は通常小さい：

Automaticを使うことは，ゼロの中央値について検定することと同じである：

対 を検定する：

中央値が μ0に近い場合， 値は通常大きい：

位置が μ0から離れている場合， 値は通常小さい：

多変量母集団の中央値ベクトルがゼロベクトルであるかどうかを検定する：

{0.1,0,-.5,0}についても検定する：

対 の検定を行う：

位置が等しくない場合， 値は通常小さい：

位置が等しい場合， 値は通常大きい：

対 の検定を行う：

データ集合の順序が検定結果に影響する：

2つの多変量母集団の中央値の差分ベクトルがゼロベクトルであるかどうかの検定を行う：

{1,0,-1,0}についても検定を行う：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

HypothesisTestDataオブジェクトから特性を抽出する：

値と検定統計：

任意数の特性を同時に抽出する：

値と検定統計：

レポート  (3)

いくつかの検定の結果を表にする：

カスタマイズしたレポート用に検定表から項目を取り出す：

値あるいは検定統計を表にする：

表の 値：

表の検定統計：

オプション  (12)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

対 を検定する：

両側検定を行う．あるいは片側検定を代りに行う：

対 を検定する：

対 を検定する：

対 を検定する：

μ0が与えられている場合に，片側検定を代りに行う：

対 を検定する：

対 を検定する：

MaxIterations  (2)

多変量検定に使う最大反復数を設定する：

デフォルトでは500回の反復が行える：

最大反復数を設定することによって，結果として共分散の不足をもたらすことがある：

値は等しくない：

Method  (4)

デフォルトでは，漸近的な検定統計分布を使って 値が計算される：

置換法が使える：

使用する置換数を設定する：

デフォルトでのランダム置換が使われる：

ランダム置換を生成するために使う種を設定する：

SignificanceLevel  (1)

有意水準は"TestConclusion"と"ShortTestConclusion"に使われる：

VerifyTestAssumptions  (2)

診断は，AllかNoneを使ってまとめて制御することができる：

すべての仮定を検証する：

どの仮定もチェックしない：

診断は個々に制御することができる：

対称性についてチェックする：

対称性の仮定をTrueに設定する：

アプリケーション  (1)

12組の一卵性双生児に対して積極性を測る心理検査が行われた．最初に生まれた双子の方が後に生まれた双子よりも積極的であることが多いという仮説が立てられた：

生まれた順序は積極性に影響を与えないという を退けるのに十分な証拠がない：

特性と関係  (8)

SignedRankTestは一般にSignTestよりも強力である：

一変量のウィルコクソン(Wilcoxon)の符号順位検定統計：

タイがないので，Orderingを使って順位を計算することができる：

漸近的な両側 値：

一変量データについては，検定統計は漸近的に正規である：

多変量データについては，検定統計は においてChiSquareDistributionに従う：

自由度はデータの次元に等しい：

多変量データについては，SignedRankTestは事実上単位球の一様性について検定を行う：

行列の空間符号順位を計算する関数：

μ0からの偏差は，空間符号順位のクラスタとより大きい検定統計を返す：

検定統計は多変量データについてアフィン不変量である：

符号順位検定は，入力がTimeSeriesのときにのみ値に使うことができる：

符号順位検定は，入力がTemporalDataのときには，すべての値に同時に使うことができる：

すべての値のみの検定を行う：

2つの経路の中央値の差についての検定を行う：

考えられる問題  (1)

SignedRankTestでは，データは共通の中央値について対称でなければならない：

データが対称ではない場合はSignTestを使う：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), SignedRankTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/SignedRankTest.html.

テキスト

Wolfram Research (2010), SignedRankTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/SignedRankTest.html.

CMS

Wolfram Language. 2010. "SignedRankTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SignedRankTest.html.

APA

Wolfram Language. (2010). SignedRankTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SignedRankTest.html

BibTeX

@misc{reference.wolfram_2024_signedranktest, author="Wolfram Research", title="{SignedRankTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SignedRankTest.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_signedranktest, organization={Wolfram Research}, title={SignedRankTest}, year={2010}, url={https://reference.wolfram.com/language/ref/SignedRankTest.html}, note=[Accessed: 25-November-2024 ]}