SpheroidalEigenvalue
SpheroidalEigenvalue[n,m,γ]
次数 ![]() で位数
で位数 ![]() の回転楕円体固有値を与える.
の回転楕円体固有値を与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- 連続する
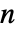 の回転楕円体固有値は,微分方程式
の回転楕円体固有値は,微分方程式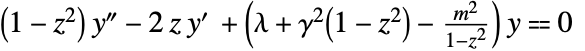 に
に 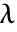 についての正規化可能な解が存在するような
についての正規化可能な解が存在するような 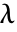 の連続する値に対応する.
の連続する値に対応する. - SpheroidalEigenvalue[n,m,0]は
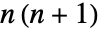 と等価である.
と等価である. - 特別な引数の場合,SpheroidalEigenvalueは,自動的に厳密値を計算する.
- SpheroidalEigenvalueは任意の数値精度で評価できる.
- SpheroidalEigenvalueは自動的にリストに縫い込まれる. »
例題
すべて開くすべて閉じる例 (4)
スコープ (14)
数値評価 (5)
MatrixFunctionを使って行列のSpheroidalEigenvalue関数を計算することもできる:
特定の値 (7)
SpheroidalEigenvalue[1,2/3,x]の最大値を求める:
m=1で γ=n π/2のときは,SpheroidalEigenvalueを評価すると厳密値になる:
SpheroidalEigenvalueは要素単位でリストに縫い込まれる:
TraditionalFormによる表示:
可視化 (2)
アプリケーション (3)
特性と関係 (1)
SpheroidalEigenvalueは,半整数値については簡約されてMathieuCharacteristicA関数になる:
考えられる問題 (1)
SpheroidalEigenvalueは ![]() の半整数値と
の半整数値と ![]() の一般的な値については評価しない:
の一般的な値については評価しない:
テキスト
Wolfram Research (2007), SpheroidalEigenvalue, Wolfram言語関数, https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html.
CMS
Wolfram Language. 2007. "SpheroidalEigenvalue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html.
APA
Wolfram Language. (2007). SpheroidalEigenvalue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpheroidalEigenvalue.html