SpheroidalS1

SpheroidalS1[n,m,γ,z]

gives the radial spheroidal function of the first kind.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The radial spheroidal functions satisfy the differential equation 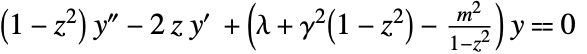with the spheroidal eigenvalue 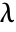given by SpheroidalEigenvalue[n,m,γ].
  • The 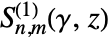are normalized according to the Meixner–Schäfke scheme.
  • SpheroidalS1 can be evaluated to arbitrary numerical precision.
  • SpheroidalS1 automatically threads over lists. »

Examples

open allclose all

Basic Examples  (5)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at a singular point:

Scope  (21)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix SpheroidalS1 function using MatrixFunction:

Specific Values  (4)

Simple exact values are generated automatically:

Find the first positive maximum of SpheroidalS1[2,0,5,x]:

SpheroidalS1 functions become elementary if m=1 and γ=n π/2 :

TraditionalForm typesetting:

Visualization  (3)

Plot the SpheroidalS1 function for integer orders:

Plot the SpheroidalS1 function for noninteger parameters:

Plot the real part of TemplateBox[{2, 0, 1, z}, SpheroidalS1]:

Plot the imaginary part of TemplateBox[{2, 0, 1, z}, SpheroidalS1]:

Function Properties  (5)

SpheroidalS1 is not an analytic function:

TemplateBox[{1, 2, {pi, /, 2}, x}, SpheroidalS1] has both singularities and discontinuities for :

TemplateBox[{1, 2, {pi, /, 2}, x}, SpheroidalS1] is neither non-decreasing nor non-increasing:

TemplateBox[{1, 2, {pi, /, 2}, x}, SpheroidalS1] is not injective:

SpheroidalS1 is neither non-negative nor non-positive:

SpheroidalS1 is neither convex nor concave:

Differentiation  (2)

First derivative with respect to z:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z when n=10, m=2 and γ=1/3:

Series Expansions  (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Taylor expansion at a generic point:

Applications  (4)

Spheroidal angular harmonics are eigenfunctions of the Sinc transform on the interval :

Plot the eigenvalue:

Find resonant frequencies for the Dirichlet problem in the prolate spheroidal cavity:

Determine the first few frequencies:

Plot the prolate and oblate functions:

Build a near-spherical approximation to :

First few terms of the approximation:

Compare numerically:

Possible Issues  (1)

Spheroidal functions do not evaluate for half-integer values of n and generic values of m:

Wolfram Research (2007), SpheroidalS1, Wolfram Language function, https://reference.wolfram.com/language/ref/SpheroidalS1.html.

Text

Wolfram Research (2007), SpheroidalS1, Wolfram Language function, https://reference.wolfram.com/language/ref/SpheroidalS1.html.

CMS

Wolfram Language. 2007. "SpheroidalS1." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpheroidalS1.html.

APA

Wolfram Language. (2007). SpheroidalS1. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpheroidalS1.html

BibTeX

@misc{reference.wolfram_2024_spheroidals1, author="Wolfram Research", title="{SpheroidalS1}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SpheroidalS1.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_spheroidals1, organization={Wolfram Research}, title={SpheroidalS1}, year={2007}, url={https://reference.wolfram.com/language/ref/SpheroidalS1.html}, note=[Accessed: 22-December-2024 ]}