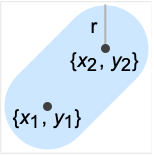
StadiumShape[{{x1,y1},{x2,y2}},r]
represents a stadium of radius r between the points {x1,y1} and {x2,y2}.


StadiumShape
StadiumShape[{{x1,y1},{x2,y2}},r]
represents a stadium of radius r between the points {x1,y1} and {x2,y2}.
Details and Options

- StadiumShape can be used as a geometric region and graphics primitive.
- StadiumShape[] is equivalent to StadiumShape[{{-1,0},{1,0}},1].
- StadiumShape[r] is equivalent to StadiumShape[{{-1,0},{1,0}},r].
- StadiumShape[{p1,p2},r] represents the region {p|RegionDistance[Line[p1,p2],p]≤r}.
- StadiumShape can be used in Graphics.
- In graphics, the points {xi,yi} can be Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, and color.
Examples
open all close allBasic Examples (5)
Get the Area of a stadium:
Scope (16)
Graphics (6)
Styling (2)
Coordinates (1)
Points can be Dynamic:
Applications (4)
Plot a function over a stadium:
Create a 3D stadium extrusion with RegionProduct:
Using a series of stadiums (and a disk), create a stick figure:
Use RotationTransform to make the stick figure's limbs pivot:
Make a spring visualization from a collection of stadiums. Make a function that creates a set of stadiums for the front half of the spring and another for the back half, given that each stadium has a horizontal component of ![]() :
:
Set the top layer of the spring to a lighter gray than the back and make it interactively stretchable using Manipulate:
Properties & Relations (6)
Disk is the limit of StadiumShape as p1 approaches p2:
The 3D version of StadiumShape is CapsuleShape:
A StadiumShape formed from the RegionUnion of disks and a rectangle:
The area is the sum of the disk and quadrilateral areas:
StadiumShape is all points no more than ![]() from a Line:
from a Line:
ImplicitRegion can represent any StadiumShape:
A thick, rounded Line looks like a StadiumShape:
See Also
Related Guides
History
Text
Wolfram Research (2015), StadiumShape, Wolfram Language function, https://reference.wolfram.com/language/ref/StadiumShape.html.
CMS
Wolfram Language. 2015. "StadiumShape." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StadiumShape.html.
APA
Wolfram Language. (2015). StadiumShape. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StadiumShape.html
BibTeX
@misc{reference.wolfram_2025_stadiumshape, author="Wolfram Research", title="{StadiumShape}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/StadiumShape.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_stadiumshape, organization={Wolfram Research}, title={StadiumShape}, year={2015}, url={https://reference.wolfram.com/language/ref/StadiumShape.html}, note=[Accessed: 26-February-2026]}