StateTransformationLinearize
StateTransformationLinearize[asys]
linearizes the AffineStateSpaceModel asys by state transformation.
StateTransformationLinearize[asys,{z,lform}]
specifies the new states z and form of linearization lform.
StateTransformationLinearize[asys,…,"prop"]
computes the property "prop".
Details and Options

- StateTransformationLinearize attempts to transform an affine system to a linear one so that linear control techniques can be used on the linearized dynamics.
- Using a state transformation x->p[z], the original affine system with dynamics
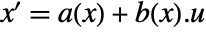 and output
and output 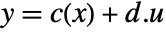 gets transformed to an input-output, input-state, or state-output linear system.
gets transformed to an input-output, input-state, or state-output linear system. - The following forms of exact linearization lform can be used:
-
Automatic automatically linearize "InputOutput" 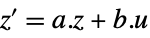 ,
, 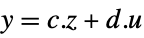
"InputState" 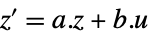 ,
, 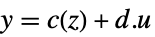
"StateOutput" 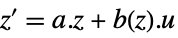 ,
, 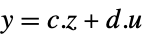
- The Automatic setting will attempt "InputOutput", "InputState", or "StateOutput".
- StateTransformationLinearize returns a LinearizingTransformationData object that can be used to extract detailed properties for further analysis and design.
- Properties related to the state transformation include:
-
"InverseStateTransformation" inverse state transformation "StateTransformation" state transformation "TransformedSystem" linearized or partially linearized transformed system tsys "Linearization" form of linearization "lform" - Properties related to controller and estimator design include:
-
{"OriginalSystemController",cs} controller for asys based on controller cs designed for tsys {"OriginalSystemEstimator",es} estimator for asys based on estimator es designed for tsys {"ClosedLoopSystem",cs} closed-loop system based on the linear controller cs
Examples
open allclose allBasic Examples (1)
Scope (12)
Basic Uses (5)
The transformed system shows that the state-to-output dynamics have been linearized:
Explicitly obtain the type of linearization:
Specify the new state variables to use:
Specify the type of linearization to use:
The input dynamics are linear, but the output is nonlinear:
Input-Output Linearize (3)
Get transformation-related properties:
Forward and inverse state transformations:
The transformed linear system:
Design controllers using exact and approximate linearization, and compare:
Design a controller and observer for the linearized system:
The simulation of the closed-loop system:
A controller based on approximate linearization, using same specifications:
Design estimators using exact and approximate linearization, and compare:
The estimator for the original system:
The trajectories of the estimated states:
An estimator based on approximate linearization, using the same specification:
The trajectories of the estimated states, based on approximate linearization:
Compute the actual state trajectories:
Compare the actual and estimated trajectories of the first state:
Compare the actual and estimated trajectories of the second state:
State-Output Linearize (2)
Get transformation-related properties:
Forward and inverse state transformations:
The transformed system with linear dynamics from state to output:
Design an estimator using exact linearization:
The estimator for the original system:
The trajectories of the estimated states:
Input-State Linearize (2)
Get transformation-related properties:
Forward and inverse state transformations:
The transformed system with linear dynamics from input to state:
Design controllers using exact and approximate linearization, and compare:
A controller based on exact linearization:
The design based on approximate linearization:
The closed-loop system with feedback, based on approximate linearization:
Properties & Relations (4)
The transformed system is related to the input system by StateSpaceTransform:
The input-output linearized system is controllable and observable:
Text
Wolfram Research (2014), StateTransformationLinearize, Wolfram Language function, https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.
CMS
Wolfram Language. 2014. "StateTransformationLinearize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.
APA
Wolfram Language. (2014). StateTransformationLinearize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateTransformationLinearize.html