WOLFRAM

Wolfram 语言与系统参考资料中心

StateTransformationLinearize[asys]

通过状态变换，线性化 AffineStateSpaceModel asys.

StateTransformationLinearize[asys,{z,lform}]

指定新状态 z 和线性化形式 lform.

StateTransformationLinearize[asys,…,"prop"]

计算属性 "prop".

更多信息和选项
Details and Options Details and Options
范例  
基本范例  
范围  
Basic Uses  
Input-Output Linearize  
State-Output Linearize  
Input-State Linearize  
属性和关系  
参见
相关指南
历史
按以下格式引用：

StateTransformationLinearize

StateTransformationLinearize[asys]

通过状态变换，线性化 AffineStateSpaceModel asys.

StateTransformationLinearize[asys,{z,lform}]

指定新状态 z 和线性化形式 lform.

StateTransformationLinearize[asys,…,"prop"]

计算属性 "prop".

更多信息和选项

  • StateTransformationLinearize 试图将一个仿射系统变换成一个线性系统，这样线性控制技术可被用在线性动态.
  • 使用一个状态变换 x->p[z]，动态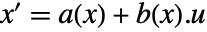为 和输出为 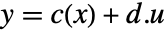的原始仿射系统会变换成输入-输出，输入-状态或状态-输出线性系统.
  • 可用以下精确线性化的形式 lform：
  • Automatic自动线性化
    "InputOutput",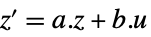
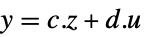
    "InputState",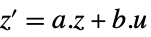
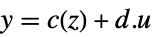
    "StateOutput",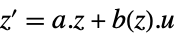
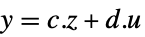
  • Automatic 设置会尝试 "InputOutput"，"InputState" 或 "StateOutput".
  • StateTransformationLinearize 返回一个 LinearizingTransformationData 对象，可以用来提取详细的属性来进一步分析和设计.
  • 与状态变换相关属性包括：
  • "InverseStateTransformation"逆状态变换
    "StateTransformation"状态变换
    "TransformedSystem"线性化或半线性化变换系统 tsys
    "Linearization"线性化形式 "lform"
  • 与控制器和估算器设计相关的属性包括：
  • {"OriginalSystemController",cs}asys 的控制器，基于为 tsys 设计的控制器 cs
    {"OriginalSystemEstimator",es}asys 的估算器，基于为 tsys 设计的估算器 es
    {"ClosedLoopSystem",cs}闭环系统，基于线性控制器 cs

范例

打开所有单元 关闭所有单元

基本范例  (1)

用状态变换线性化一个仿射系统：

变换后的系统是完全线性的：

用线性系统计算系统的反馈增益：

闭环系统：

该闭环系统是稳定的：

范围  (12)

Basic Uses  (5)

线性化仿射系统：

变换后的系统显示状态到输出的动态已经被线性化：

显式获得线性化的类型：

指定要用的新的状态变量：

指定要用的线性化的类型：

输入动态为线性，但是输出是非线性：

预先指定属性：

可指定多个属性：

指定几个属性：

Input-Output Linearize  (3)

获得与变换相关的属性：

正向状态变换与逆向状态变换：

变换后的线性系统：

用精确和近似线性化设计控制器并做比较：

变换后的系统：

设计线性系统的控制器和观测器：

闭环系统：

对闭环系统的模拟：

基于近似线性化的控制器（用同样的规范）：

模拟该系统：

比较响应：

用精确和近似线性化设计估算器并做比较：

变换后的系统：

原始系统的估算器：

估算状态的轨迹：

基于近似线性化的估算器（用同样的规范）：

估算状态的轨迹，基于近似线性化：

计算实际状态轨迹：

比较第一状态的实际和估算轨迹：

比较第二状态的实际和估算轨迹：

State-Output Linearize  (2)

获得变换相关的属性：

正向状态变换与逆向状态变换：

变换后具有线性动态（从状态到输出）的系统：

用精确线性化设计一个估算器：

变换后的系统：

对原始系统的估算器：

估算状态的轨迹：

实际状态轨迹：

比较估算和实际状态轨迹：

Input-State Linearize  (2)

获得变换相关的属性：

正向状态变换和逆向状态变换：

变换后具有线性动态（从输入到状态）的系统：

用精确和近似线性化设计控制器并做比较：

变换后的系统：

基于精确线性化的控制器：

闭环系统：

基于近似线性化的设计：

有反馈的闭环系统，基于近似线性化：

比较两种设计：

属性和关系  (4)

变换后的系统与输入系统通过 StateSpaceTransform 相关联：

输入-输出线性化是可控制和观测的：

状态-输入线性化系统是可观测的：

输入-状态线性化系统是可控制的：

Wolfram Research (2014)，StateTransformationLinearize，Wolfram 语言函数，https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.

文本

Wolfram Research (2014)，StateTransformationLinearize，Wolfram 语言函数，https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.

CMS

Wolfram 语言. 2014. "StateTransformationLinearize." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.

APA

Wolfram 语言. (2014). StateTransformationLinearize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StateTransformationLinearize.html 年

BibTeX

@misc{reference.wolfram_2025_statetransformationlinearize, author="Wolfram Research", title="{StateTransformationLinearize}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateTransformationLinearize.html}", note=[Accessed: 24-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_statetransformationlinearize, organization={Wolfram Research}, title={StateTransformationLinearize}, year={2014}, url={https://reference.wolfram.com/language/ref/StateTransformationLinearize.html}, note=[Accessed: 24-October-2025]}