WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

SymletWavelet
✖
SymletWavelet

✖

represents the Symlet wavelet of order 4.

✖

represents the Symlet wavelet of order n.

Details

  • SymletWavelet, also known as "least asymmetric" wavelet, defines a family of orthogonal wavelets.
  • SymletWavelet[n] is defined for any positive integer n.
  • The scaling function (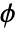) and wavelet function (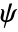) have compact support length of 2n. The scaling function has n vanishing moments.
  • SymletWavelet can be used with such functions as DiscreteWaveletTransform and WaveletPhi, etc.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Scaling function:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4lu6z4
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-gb8f9b
Out[2]=2

Wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-vc7o0g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-xdbxfp
Out[2]=2

Filter coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-kjry2h
Out[1]=1

Scope  (14)Survey of the scope of standard use cases

Basic Uses  (8)

Compute primal lowpass filter coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-x5t4az
Out[1]=1

Primal highpass filter coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-kigfti
Out[1]=1

Lifting filter coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-nxqmse
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-k9eeea
Out[2]=2

Generate a function to compute lifting wavelet transform:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-nfjqzn
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-ol7ejo
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-7bq5gu
Out[3]=3

Symlet scaling function of order 4:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-vl9zbf
Out[1]=1

SymletWavelet of order 10:

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4ybkxk
Out[2]=2

Plot scaling function using different levels of recursion:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-si6qgc
Out[1]=1

Symlet wavelet function of order 4:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-zncr2c
Out[1]=1

SymletWavelet of order 10:

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-duatsf
Out[2]=2

Plot scaling function using different levels of recursion:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-e43yvf
Out[1]=1

Wavelet Transforms  (5)

Compute a DiscreteWaveletTransform:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-t8skl0
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-2kxsqf
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-xhbmxi
Out[3]=3

View the tree of wavelet coefficients:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-gtqy6c
Out[4]=4

Get the dimensions of wavelet coefficients:

In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-mrjnjd
Out[5]=5

Plot the wavelet coefficients:

In[6]:=6
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-vkcd9f
Out[6]=6

Compute a DiscreteWaveletPacketTransform:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-o34j9k
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-vtrxi2
Out[2]=2

View the tree of wavelet coefficients:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-j3n0f1
Out[3]=3

Get the dimensions of wavelet coefficients:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-wuwmcl
Out[4]=4

Plot the wavelet coefficients:

In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-15wf00
Out[5]=5

Compute a StationaryWaveletTransform:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-h4s71h
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-lgbd1m

View the tree of wavelet coefficients:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-jbb9sz
Out[3]=3

Get the dimensions of wavelet coefficients:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-msff83
Out[4]=4

Plot the wavelet coefficients:

In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-yakm1p
Out[5]=5

Compute a StationaryWaveletPacketTransform:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-gbl37f
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4fxpz9

View the tree of wavelet coefficients:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-9rgpx
Out[3]=3

Get the dimensions of wavelet coefficients:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-ngfrzh
Out[4]=4

Plot the wavelet coefficients:

In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-q5dqbp
Out[5]=5

Compute a LiftingWaveletTransform:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4t2boe
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-6vbut6

View the tree of wavelet coefficients:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-xwj8z0
Out[3]=3

Get the dimensions of wavelet coefficients:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-56ffkm
Out[4]=4

Plot the wavelet coefficients:

In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-vyacdo
Out[5]=5

Higher Dimensions  (1)

Multivariate scaling and wavelet functions are products of univariate ones:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-rk8e1w
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-tvf11
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-yf2o9
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-s16yjj
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-gmiius
Out[5]=5

Applications  (3)Sample problems that can be solved with this function

Approximate a function using Haar wavelet coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-0yl9y

Perform a LiftingWaveletTransform:

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-6b212t

Approximate original data by keeping n largest coefficients and thresholding everything else:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-btzo2q

Compare the different approximations:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-j4qkd4
Out[4]=4

Compute the multiresolution representation of a signal containing an impulse:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4t63
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-ft7r2g
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-fea5og
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-b5odvr
Out[4]=4

Compare the cumulative energy in a signal and its wavelet coefficients:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-vo8pov
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-p7milv
Out[2]=2

Compute the ordered cumulative energy in the signal:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-d0i4sz
In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-hqrz4
Out[4]=4

The energy in the signal is captured by relatively few wavelet coefficients:

In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-7htmqa
In[6]:=6
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-dfvj8p
In[7]:=7
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-ck6x5d
Out[7]=7

Properties & Relations  (12)Properties of the function, and connections to other functions

Order 1 SymletWavelet is equivalent to HaarWavelet:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4rcqes
Out[1]=1

Lowpass filter coefficients sum to unity; :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-v1t5fi
Out[1]=1

Highpass filter coefficients sum to zero; :

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-jrlqqz
Out[2]=2

Scaling function integrates to unity; :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-8k86sm
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-f8fecv
Out[2]=2

In particular, :

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-rnixhk
Out[3]=3

Wavelet function integrates to zero; :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-dasw6s
Out[1]=1

Wavelet function is orthogonal to the scaling function at the same scale; :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4ds4zb
Out[1]=1

The lowpass and highpass filter coefficients are orthogonal; :

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-8vwdxn
Out[2]=2

Order n of SymletWavelet indicates n vanishing moments; :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-61g7p
Out[1]=1

This means linear signals are fully represented in the scaling functions part ({0}):

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-i34fvs
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-fxiicw
Out[3]=3

Quadratic or higher-order signals are not:

In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-bspdch
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-bpn9vr
Out[5]=5

satisfies the recursion equation :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-yjbxzh
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-h6wmys

Plot the components and the sum of the recursion:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-c986c4
In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-jgy4v3
Out[4]=4

satisfies the recursion equation :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-3enc2f
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-bux40a

Plot the components and the sum of the recursion:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4clwfm
In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-p99dtx
Out[4]=4

Frequency response for is given by :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-y5x0mm

The filter is a lowpass filter:

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-za6vn3
Out[2]=2

The higher the order n, the flatter the response function at the ends:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-9czcnb
Out[3]=3

Fourier transform of is given by :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-idptzz
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-8bpbkv
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-q7ttix
Out[3]=3

Frequency response for is given by :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-fujnuf

The filter is a highpass filter:

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-s5vizp
Out[2]=2

The higher the order n, the flatter the response function at the ends:

In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-md9rn9
Out[3]=3

Fourier transform of is given by :

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-4ndhmw
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-8z0zd4
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-xhsirg
In[4]:=4
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-828qse
Out[4]=4

Possible Issues  (1)Common pitfalls and unexpected behavior

SymletWavelet is restricted to n less than 20:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-5wyn6y
Out[1]=1

SymletWavelet is not defined when n is not a positive machine integer:

In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-2551ne
Out[2]=2

Neat Examples  (2)Surprising or curious use cases

Plot translates and dilations of scaling function:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-yz9dxl
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-evsjio
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-p5xgws
Out[3]=3

Plot translates and dilations of wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-iu0uje
In[2]:=2
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-b9ooxs
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tpyx5hxzgm7qu-hts69i
Out[3]=3
Wolfram Research (2010), SymletWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/SymletWavelet.html.
✖
Wolfram Research (2010), SymletWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/SymletWavelet.html.

Text

Wolfram Research (2010), SymletWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/SymletWavelet.html.

✖
Wolfram Research (2010), SymletWavelet, Wolfram Language function, https://reference.wolfram.com/language/ref/SymletWavelet.html.

CMS

Wolfram Language. 2010. "SymletWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymletWavelet.html.

✖
Wolfram Language. 2010. "SymletWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymletWavelet.html.

APA

Wolfram Language. (2010). SymletWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymletWavelet.html

✖
Wolfram Language. (2010). SymletWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymletWavelet.html

BibTeX

@misc{reference.wolfram_2025_symletwavelet, author="Wolfram Research", title="{SymletWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SymletWavelet.html}", note=[Accessed: 29-April-2025 ]}

✖
@misc{reference.wolfram_2025_symletwavelet, author="Wolfram Research", title="{SymletWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SymletWavelet.html}", note=[Accessed: 29-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_symletwavelet, organization={Wolfram Research}, title={SymletWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/SymletWavelet.html}, note=[Accessed: 29-April-2025 ]}

✖
@online{reference.wolfram_2025_symletwavelet, organization={Wolfram Research}, title={SymletWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/SymletWavelet.html}, note=[Accessed: 29-April-2025 ]}