TitsGroupT
represents the simple Tits group ![]() .
.
Background & Context
- TitsGroupT[] represents the Tits group
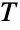 , sometimes also denoted
, sometimes also denoted 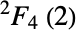 , which is a group of order
, which is a group of order ![TemplateBox[{2, 11}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].13 TemplateBox[{2, 11}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].13](Files/TitsGroupT.en/4.png) . The default representation of TitsGroupT is as a permutation group on the symbols
. The default representation of TitsGroupT is as a permutation group on the symbols 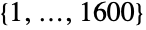 having two generators.
having two generators. - The Tits group was first introduced in the mid-1960s by mathematician Jacques Tits as the (simple) derived subgroup of the (non-simple) Ree group
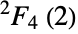 of Lie type. Because
of Lie type. Because 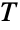 is not strictly a group of Lie type, it is sometimes regarded as a 27
is not strictly a group of Lie type, it is sometimes regarded as a 27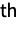 sporadic simple group. The Tits group can be realized as a maximal subgroup of the Fischer group
sporadic simple group. The Tits group can be realized as a maximal subgroup of the Fischer group 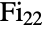 . In addition to its default permutation representation, it can be defined in terms of generators and relations as
. In addition to its default permutation representation, it can be defined in terms of generators and relations as 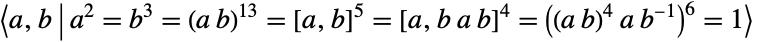 , where
, where 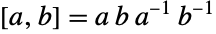 .
. - The usual group theoretic functions may be applied to TitsGroupT[], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the Tits group are available via FiniteGroupData["Tits","prop"].
- When considered together with the "true" sporadic finite simple groups, TitsGroupT[] is considered a "pariah" even though it occurs as a subquotient of MonsterGroupM (which is the criterion whose failure makes JankoGroupJ1, JankoGroupJ3, JankoGroupJ4, LyonsGroupLy, ONanGroupON and RudvalisGroupRu "pariahs").
Examples
Wolfram Research (2010), TitsGroupT, Wolfram Language function, https://reference.wolfram.com/language/ref/TitsGroupT.html.
Text
Wolfram Research (2010), TitsGroupT, Wolfram Language function, https://reference.wolfram.com/language/ref/TitsGroupT.html.
CMS
Wolfram Language. 2010. "TitsGroupT." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TitsGroupT.html.
APA
Wolfram Language. (2010). TitsGroupT. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TitsGroupT.html