gives the n×n Toeplitz matrix with first row and first column being successive integers.
ToeplitzMatrix[{c1,c2,…,cn}]
gives the Toeplitz matrix whose first column consists of entries c1, c2, ….
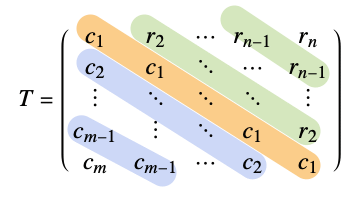
ToeplitzMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
gives the Toeplitz matrix with entries ci down the first column, and ri across the first row.


ToeplitzMatrix
gives the n×n Toeplitz matrix with first row and first column being successive integers.
ToeplitzMatrix[{c1,c2,…,cn}]
gives the Toeplitz matrix whose first column consists of entries c1, c2, ….
ToeplitzMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
gives the Toeplitz matrix with entries ci down the first column, and ri across the first row.
Details and Options


- Toeplitz matrices typically occur in applications related to approximation theory, signal processing, statistics and time series.
- A Toeplitz matrix is a matrix that is constant along its diagonals. The entries of the Toeplitz matrix
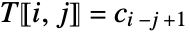 are given by
are given by 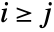 if
if 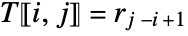 , and
, and 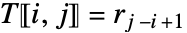 otherwise.
otherwise. - The entry r1 must be the same as c1. »
- ToeplitzMatrix[…,TargetStructure->struct] returns the Toeplitz matrix in the format specified by struct. Possible settings include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Structured" represent the matrix as a structured array "Symmetric" represent the matrix as a symmetric matrix - With ToeplitzMatrix[…,TargetStructureAutomatic], a dense matrix is returned if the number of matrix entries is less than a preset threshold, and a structured array is returned otherwise.
- For a structured ToeplitzMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"ColumnVector" vector of entries down the first column "RowVector" vector of entries across the first row "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[ToeplitzMatrix[…]] converts the structured Toeplitz matrix to an ordinary matrix.
Examples
open all close allBasic Examples (3)
Scope (9)
Make a Toeplitz matrix of machine numbers:
Make a Toeplitz matrix with 20-digit precision:
Toeplitz matrices with complex entries:
Rectangular Toeplitz matrices:
A common symbolic notation for Toeplitz matrices:
Generate a structured Toeplitz matrix:
The structured representation typically uses much less memory:
ToeplitzMatrix objects include properties that give information about the array:
The "ColumnVector" property gives the first column of the Toeplitz matrix:
The "RowVector" property gives the first row of the Toeplitz matrix:
The "Summary" property gives a brief summary of information about the array:
The "StructuredAlgorithms" property lists the functions that have structured algorithms:
When appropriate, structured algorithms return another ToeplitzMatrix object:
The transpose is also a ToeplitzMatrix:
The product of a Toeplitz matrix and its transpose is no longer a Toeplitz matrix:
Convert a dense Toeplitz matrix to a structured Toeplitz matrix:
Options (2)
TargetStructure (2)
Return the Toeplitz matrix as a dense matrix:
Return the Toeplitz matrix as a structured array:
Return the Toeplitz matrix as a symmetric matrix:
With the setting TargetStructureAutomatic, a dense matrix is returned for small dimensions:
For large dimensions, a structured representation is returned:
Applications (10)
Define a function for constructing a circulant matrix from a vector:
Multiplying a circulant matrix with a vector can be expressed as a cyclic convolution:
Multiplying a vector with a circulant matrix can be expressed as a cyclic correlation:
Circulant matrices can be diagonalized by the Fourier matrix:
The diagonal elements of the resulting diagonal matrix are the same as the product of the Fourier matrix and the starting vector, up to a constant scaling factor:
A Toeplitz matrix with symbolic entries:
The inverse of a Toeplitz matrix can be determined from just the first and last column of the inverse. Use LinearSolve to compute the first column of the inverse:
Compute the last column of the inverse:
The Gohberg–Semencul formula for the inverse of a Toeplitz matrix uses the first and last columns to assemble the full inverse matrix:
Define a tridiagonal Toeplitz matrix:
Verify an expression for the characteristic polynomial in terms of the Chebyshev polynomial of the second kind for the first few cases:
A tridiagonal Toeplitz matrix can be diagonalized by a diagonal rescaling of the type 1 discrete sine transform matrix:
Define the Kac–Murdock–Szegő (KMS) matrix as a ToeplitzMatrix:
The KMS matrix is a symmetric Toeplitz matrix:
The KMS matrix is the correlation matrix of an autoregressive process of order one (i.e. an AR(1) process):
The inverse of the KMS matrix is a tridiagonal matrix:
The characteristic polynomial of the KMS matrix can be expressed in terms of the Chebyshev polynomial of the second kind:
Define the Parter matrix as a ToeplitzMatrix:
The Parter matrix is both a Toeplitz matrix and a Cauchy matrix:
The Parter matrix's dominant singular values are clustered around ![]() :
:
The prolate matrix is a symmetric positive-definite Toeplitz matrix that appears in multitaper power spectral density estimation:
Visualize the entries of the prolate matrix:
The condition number increases exponentially with n:
The 2-norm condition number is the ratio of largest to smallest eigenvalue due to symmetry:
The daily exchange rates of the euro to the dollar from May 2012 through September 2012:
Fit an order-3 autoregressive process (ARProcess) to the exchange rates by solving the Yule-Walker equations:
The same result can be obtained from EstimatedProcess:
The order ![]() Padé approximant of a function
Padé approximant of a function ![]() about the point x=x0 can be obtained from the power series coefficients. Define the function, the numerator and denominator degrees, and the expansion point:
about the point x=x0 can be obtained from the power series coefficients. Define the function, the numerator and denominator degrees, and the expansion point:
Generate the coefficients of the power series up to order ![]() :
:
The coefficients of the denominator can be obtained by solving a Toeplitz system constructed from the power series coefficients:
The coefficients of the numerator can be obtained by multiplying the vector of denominator coefficients with a Toeplitz matrix constructed from the power series coefficients:
Assemble the Padé approximant:
Compare with the result of PadeApproximant:
Generate the first few signed elementary symmetric polynomials in ![]() variables:
variables:
Generate the first few power sums in ![]() variables:
variables:
Verify the Newton–Girard formulas [MathWorld] relating power sums and elementary symmetric polynomials:
Define the Ching matrix as a ToeplitzMatrix:
The Ching matrix is a lower Hessenberg 0-1 matrix (a matrix with entries that are either zero or one, and is zero above the first superdiagonal):
The determinant of the order n Ching matrix is equal to the n![]() Fibonacci number, and gives an upper bound for the determinant of all lower Hessenberg 0-1 matrices:
Fibonacci number, and gives an upper bound for the determinant of all lower Hessenberg 0-1 matrices:
Properties & Relations (5)
The determinant of the Toeplitz matrix of size ![]() is
is ![]() :
:
Cyclic ListConvolve with zero padding is equivalent to multiplication with a lower triangular Toeplitz matrix:
Cyclic ListCorrelate with zero padding is equivalent to multiplication with an upper triangular Toeplitz matrix:
ToeplitzMatrix[{c1,c2,…}] is Hermitian if c1 is real:
![]() is diagonalizable by a unitary matrix:
is diagonalizable by a unitary matrix:
ToeplitzMatrix and HankelMatrix are related by multiplication with an exchange matrix (a reversed identity matrix):
Equivalently, reversing a Toeplitz matrix gives a Hankel matrix:
Related Guides
Text
Wolfram Research (2007), ToeplitzMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/ToeplitzMatrix.html (updated 2024).
CMS
Wolfram Language. 2007. "ToeplitzMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ToeplitzMatrix.html.
APA
Wolfram Language. (2007). ToeplitzMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ToeplitzMatrix.html
BibTeX
@misc{reference.wolfram_2025_toeplitzmatrix, author="Wolfram Research", title="{ToeplitzMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ToeplitzMatrix.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_toeplitzmatrix, organization={Wolfram Research}, title={ToeplitzMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/ToeplitzMatrix.html}, note=[Accessed: 08-January-2026]}