HankelMatrix[n]
gives the n×n Hankel matrix with first row and first column being successive integers.
HankelMatrix[{c1,c2,…,cn}]
gives the Hankel matrix whose first column consists of entries c1, c2, ….
HankelMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
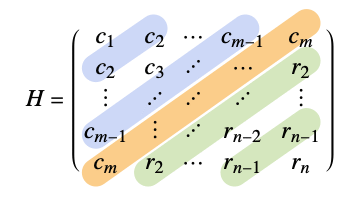
gives the Hankel matrix with entries ci down the first column, and ri across the last row.


HankelMatrix
HankelMatrix[n]
gives the n×n Hankel matrix with first row and first column being successive integers.
HankelMatrix[{c1,c2,…,cn}]
gives the Hankel matrix whose first column consists of entries c1, c2, ….
HankelMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
gives the Hankel matrix with entries ci down the first column, and ri across the last row.
Details and Options


- Hankel matrices typically occur in applications related to approximation theory, functional analysis, numerical analysis and signal processing.
- A Hankel matrix is a matrix that is constant along its antidiagonals. The entries of the Hankel matrix
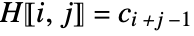 are given by
are given by 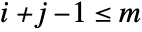 if
if 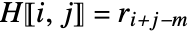 , and
, and 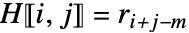 otherwise.
otherwise. - The entry cm must be the same as r1. »
- For m=n, the Hankel matrix is a symmetric matrix and will have real eigenvalues if the entries ci and rj are all real.
- HankelMatrix[…,TargetStructure->struct] returns the Hankel matrix in the format specified by struct. Possible settings include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Structured" represent the matrix as a structured array "Symmetric" represent the matrix as a symmetric matrix - With HankelMatrix[…,TargetStructureAutomatic], a dense matrix is returned if the number of matrix entries is less than a preset threshold, and a structured array is returned otherwise.
- For a structured HankelMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"ColumnVector" vector of entries down the first column "RowVector" vector of entries across the last row "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[HankelMatrix[…]] converts the structured Hankel matrix to an ordinary matrix.
Examples
open all close allBasic Examples (3)
Scope (9)
Make a Hankel matrix of machine numbers:
Make a Hankel matrix with 20-digit precision:
Hankel matrices with complex entries:
A common symbolic notation for Hankel matrices:
Generate a structured Hankel matrix:
The structured representation typically uses much less memory:
HankelMatrix objects include properties that give information about the array:
The "ColumnVector" property gives the first column of the Hankel matrix:
The "RowVector" property gives the last row of the Hankel matrix:
The "Summary" property gives a brief summary of information about the array:
The "StructuredAlgorithms" property lists the functions that have structured algorithms:
When appropriate, structured algorithms return another HankelMatrix object:
The transpose is also a HankelMatrix:
The product of a Hankel matrix and its transpose is no longer a Hankel matrix:
Convert a dense Hankel matrix to a structured Hankel matrix:
Options (2)
TargetStructure (2)
Return the Hankel matrix as a dense matrix:
Return the Hankel matrix as a structured array:
Return the Hankel matrix as a symmetric matrix:
With the setting TargetStructureAutomatic, a dense matrix is returned for small dimensions:
For large dimensions, a structured representation is returned:
Applications (4)
The order ![]() Padé approximant can computed using Hankel determinants. Generate the first 2n+1 partial sums of the power series for Exp[z]:
Padé approximant can computed using Hankel determinants. Generate the first 2n+1 partial sums of the power series for Exp[z]:
Take the second differences of the partial sums:
The Shanks transformation expresses the order ![]() Padé approximant as a ratio of two Hankel determinants:
Padé approximant as a ratio of two Hankel determinants:
Compare with the result of PadeApproximant:
An n-term sum of exponential functions:
Sample the exponential function at ![]() points:
points:
Use Prony's method [Wikipedia] to recover the sum of exponentials from the data:
Determinants of Hankel matrices appear in the continued fraction expansion of functions. Generate the first few series expansion coefficients of a function:
Define a utility function for building Hankel determinants out of series coefficients:
Generate the first few coefficients for a continued fraction expansion:
Construct the continued fraction approximation:
Compare the continued fraction with the original function:
The n-point Gaussian quadrature rule corresponding to a weight function ![]() over the interval
over the interval ![]() can be derived from the moments of the weight function. Define a weight function and an interval:
can be derived from the moments of the weight function. Define a weight function and an interval:
Generate the first ![]() moments starting from 0:
moments starting from 0:
The coefficients of the n![]() -order orthogonal polynomial corresponding to the given weight function can be obtained by solving a Hankel system constructed from the moments:
-order orthogonal polynomial corresponding to the given weight function can be obtained by solving a Hankel system constructed from the moments:
The nodes of the n-point Gaussian quadrature rule are the roots of the orthogonal polynomial:
The weights of the n-point Gaussian quadrature rule can be obtained by solving a Vandermonde system:
Use the nodes and weights to numerically approximate an integral:
Compare with the answer obtained from NIntegrate:
Properties & Relations (6)
The determinant of the Hankel matrix of size ![]() is
is ![]() :
:
A square Hankel matrix with real entries is symmetric:
HankelMatrix[c,RotateRight[c]] is a square anticirculant matrix:
Square anticirculant matrices have eigenvector {1,…} with eigenvalue c1+c2+…:
HankelMatrix and ToeplitzMatrix are related by multiplication with an exchange matrix (a reversed identity matrix):
Equivalently, reversing a Hankel matrix gives a Toeplitz matrix:
Demonstrate a factorization of the inverse of a Vandermonde matrix in terms of diagonal, Vandermonde and Hankel matrices:
Express a Cauchy matrix as a product of diagonal, Vandermonde and Hankel matrices:
Neat Examples (3)
Visualize the entries of the Hankel matrix:
Define a Hankel matrix whose entries are the reciprocals of the factorials:
Its determinant can be expressed in terms of the Barnes G-function:
Define a Hankel matrix whose entries are the Bernoulli numbers:
Its determinant can be expressed in terms of the Barnes G-function:
Related Guides
Text
Wolfram Research (2007), HankelMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/HankelMatrix.html (updated 2024).
CMS
Wolfram Language. 2007. "HankelMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/HankelMatrix.html.
APA
Wolfram Language. (2007). HankelMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HankelMatrix.html
BibTeX
@misc{reference.wolfram_2025_hankelmatrix, author="Wolfram Research", title="{HankelMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HankelMatrix.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_hankelmatrix, organization={Wolfram Research}, title={HankelMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HankelMatrix.html}, note=[Accessed: 24-February-2026]}