第1行と第1列が連続する整数である n×n のテプリッツ(Toeplitz)行列を返す.
ToeplitzMatrix[{c1,c2,…,cn}]
第1列が成分 c1, c2, …からなるテプリッツ行列を返す.
ToeplitzMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
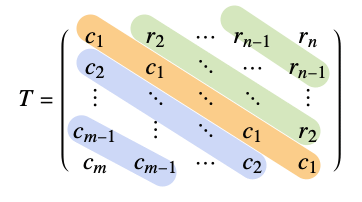
第1列の成分が ci,第1行の成分が riのテプリッツ行列を返す.


ToeplitzMatrix
第1行と第1列が連続する整数である n×n のテプリッツ(Toeplitz)行列を返す.
ToeplitzMatrix[{c1,c2,…,cn}]
第1列が成分 c1, c2, …からなるテプリッツ行列を返す.
ToeplitzMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
第1列の成分が ci,第1行の成分が riのテプリッツ行列を返す.
詳細とオプション


- テプリッツ行列は,通常,近似理論,信号処理,統計,時系列等に関連した応用で使われる.
- テプリッツ行列は,その対角に沿って一定の行列である.テプリッツ行列
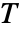 の成分は,
の成分は,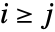 のときは
のときは 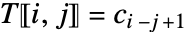 で,それ以外のときは
で,それ以外のときは 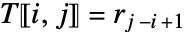 で与えられる.
で与えられる. - 成分 r1は成分 s c1と等しくなければならない. »
- ToeplitzMatrix[…,TargetStructure->struct]はテプリッツ行列を struct で指定された形式で返す.次は,
-
Automatic 返す際の表現を自動選択する "Dense" 行列を密な行列として表す "Structured" 行列を構造化配列として表す "Symmetric" 行列を対称行列として表す - With ToeplitzMatrix[…,TargetStructureAutomatic]の設定では,行列の成分数が設定された閾値未満の場合は密な行列が返され,それ以外の場合は構造化配列が返される.
- 構造化されたToeplitzMatrix sa は,次の特性"prop"に sa["prop"]でアクセスできる.
-
"ColumnVector" 第1列の成分のベクトル "RowVector" 第1行の成分のベクトル "Properties" サポートされる特性のリスト "Structure" 構造化配列の型 "StructuredData" 構造化配列で保存されている内部データ "StructuredAlgorithms" 構造化配列に対して特別なメソッドを持つ関数のリスト "Summary" Datasetとして表される要約情報 - Normal[ToeplitzMatrix[…]]は構造化テプリッツ行列を通常の行列に変換する.
例題
すべて開く すべて閉じるスコープ (9)
ToeplitzMatrixオブジェクトには配列についての情報を与える特性が含まれている:
"ColumnVector"特性はテプリッツ行列の第1列を与える:
"RowVector"特性はテプリッツ行列の第1行を与える:
"Summary"特性は配列についての情報の簡単な要約を与える:
"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数のリストを与える:
構造化アルゴリズムは,適切な場合は別のToeplitzMatrixオブジェクトを返す:
転置もまたToeplitzMatrixである:
オプション (2)
TargetStructure (2)
TargetStructureAutomaticの設定のとき,次元が小さい場合は密な行列が返される:
アプリケーション (10)
巡回行列とベクトルの乗算は巡回たたみ込みとして表すことができる:
結果の対角行列の対角要素はフーリエ行列と開始ベクトルの積に定倍率まで等しい:
テプリッツ行列の逆行列は逆行列の最初と最後の列だけから決定できる.LinearSolveを使って逆行列の最初の列を計算する:
テプリッツ行列の逆行列についてのGohberg–Semenculの公式は,最初と最後の列を使って完全な逆行列を組み立てる:
固有多項式についての式を最初のいくつかの第2種チェビシェフ(Chebyshev)多項式によって確かめる:
三重対角テプリッツ行列は1型の離散正弦変換行列の対角リスケーリングによって対角化できる:
Kac–Murdock–Szegő(KMS)行列をToeplitzMatrixとして定義する:
KMS行列は,一次自己回帰過程の相関行列(つまり,AR(1)過程)である:
KMS行列の固有多項式は第2種チェビシェフ多項式で表すことができる:
Parter行列をToeplitzMatrixとして定義する:
Parter行列はテプリッツ行列でもりコーシー行列でもある:
Parter行列の支配的特異値は ![]() の周りにクラスタ化している:
の周りにクラスタ化している:
prolate matrix(扁長行列)は,マルチテーパーパワースペクトル密度推定に現れる対称正定値テプリッツ行列である:
2ノルム条件数は対称性による最大固有値と最小固有値の比である:
2012年5月から2012年9月までのユーロとドルの毎日の為替レート:
Yule-Walker方程式を解くことで,3次自己回帰過程(ARProcess) を為替レートにフィットする:
EstimatedProcessを使っても同じ結果が得られる:
点 x=x0に関する関数 ![]() の次数
の次数![]() パデ(Padé)近似はベキ級数係数から取得できる.関数,分子と分母の次数,展開点を定義する:
パデ(Padé)近似はベキ級数係数から取得できる.関数,分子と分母の次数,展開点を定義する:
分母の係数はベキ級数係数から構築されたテプリッツ系を解くことで入手できる:
分子の係数は分母の係数のベクトルにベキ級数係数から構築されたテプリッツ行列を掛けることで入手できる:
PadeApproximantの結果と比較する:
最初のいくつかの符号付き初等対称多項式を ![]() 個の変数で生成する:
個の変数で生成する:
ベキ乗和と初等対称多項式に関連するNewton–Girardの公式[MathWorld]を確認する:
Ching行列をToeplitzMatrixとして定義する:
Ching行列は下ヘッセンベルク(Hessenberg)0-1行列(成分か0か1で最初の上対角の上が0の行列)である:
n 次Ching行列の行列式は n![]() 番目のフィボナッチ(Fibonacci)数と同じであり,すべての下ヘッセンべルック0-1行列の上界を与える:
番目のフィボナッチ(Fibonacci)数と同じであり,すべての下ヘッセンべルック0-1行列の上界を与える:
特性と関係 (5)
充填のない巡回ListConvolveは下三角テプリッツ行列による乗算に等しい:
充填のない巡回ListCorrelateは上三角テプリッツ行列による乗算に等しい:
ToeplitzMatrix[{c1,c2,…}]は,c1 が実数の場合はハミルトン行列である:
ToeplitzMatrixとHankelMatrixは交換行列(逆恒等行列)との乗算によって関連している:
テキスト
Wolfram Research (2007), ToeplitzMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/ToeplitzMatrix.html (2024年に更新).
CMS
Wolfram Language. 2007. "ToeplitzMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ToeplitzMatrix.html.
APA
Wolfram Language. (2007). ToeplitzMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ToeplitzMatrix.html
BibTeX
@misc{reference.wolfram_2025_toeplitzmatrix, author="Wolfram Research", title="{ToeplitzMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/ToeplitzMatrix.html}", note=[Accessed: 04-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_toeplitzmatrix, organization={Wolfram Research}, title={ToeplitzMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/ToeplitzMatrix.html}, note=[Accessed: 04-February-2026]}