UnilateralConvolve
UnilateralConvolve[f,g,u,t]
式 f と g の u についての片側たたみ込みを与える.
UnilateralConvolve[f,g,{u1,…,un},{t1,…,tn}]
多次元片側たたみ込みを与える.
詳細とオプション

- UnilateralConvolveは,因果たたみ込みとしても知られている.
- 片側たたみ込みの概念は,因果系の研究から自然発生した.そのような系の任意の時点における出力は過去と現在の時点における入力の値のみに依存する.
- 2つの関数
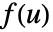 と
と 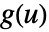 の片側たたみ込み
の片側たたみ込み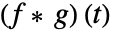 は
は 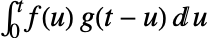 で与えられる.
で与えられる. - 積分の下限は,事実上,
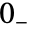 であるとみなされるので,
であるとみなされるので,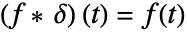 である.ただし,
である.ただし,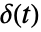 はDiracDelta関数である.
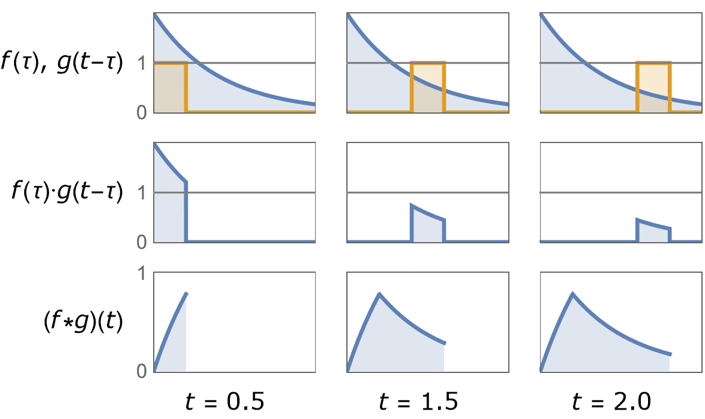
はDiracDelta関数である. - 以下は指数関数と単位ボックス関数の片側たたみ込みを示している.
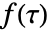 は指数関数を,
は指数関数を,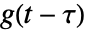 は鏡映・シフトされた単位ボックス関数を表す.たたみ込み
は鏡映・シフトされた単位ボックス関数を表す.たたみ込み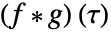 は
は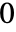 から
から 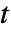 までの積
までの積 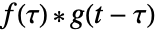 の下の面積である.
の下の面積である. - 多次元たたみ込みは
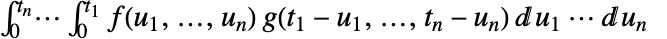 で与えられる.
で与えられる. - 次は,使用可能なオプションである.
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を生成するかどうか Method Automatic 使用するメソッド PrincipalValue False 主値積分を使うかどうか
例題
すべて開くすべて閉じる例 (3)
スコープ (5)
アプリケーション (3)
特性と関係 (7)
UnilateralConvolveは有限区間での積分を計算する:
DiracDeltaを使ったたたみ込みは関数それ自体を与える:
入力関数が因果関係を示すとき,ConvolveはUnilateralConvolveと一致する:
Wolfram Research (2024), UnilateralConvolve, Wolfram言語関数, https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
テキスト
Wolfram Research (2024), UnilateralConvolve, Wolfram言語関数, https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
CMS
Wolfram Language. 2024. "UnilateralConvolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnilateralConvolve.html.
APA
Wolfram Language. (2024). UnilateralConvolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnilateralConvolve.html