LaplaceTransform

LaplaceTransform[f[t],t,s]

gives the symbolic Laplace transform of f[t] in the variable t and returns a transform F[s] in the variable s.

LaplaceTransform[f[t],t,]

gives the numeric Laplace transform at the numerical value .

LaplaceTransform[f[t1,…,tn],{t1,…,tn},{s1,…,sn}]

gives the multidimensional Laplace transform of f[t1,…,tn].

Details and Options

  • Laplace transforms are typically used to transform differential and partial differential equations to algebraic equations, solve and then inverse transform back to a solution.
  • Laplace transforms are also extensively used in control theory and signal processing as a way to represent and manipulate linear systems in the form of transfer functions and transfer matrices. The Laplace transform and its inverse are then a way to transform between the time domain and frequency domain.
  • The Laplace transform of a function 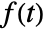is defined to be .
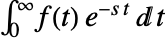  • The multidimensional Laplace transform is given by .
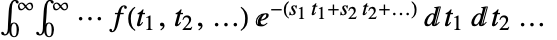  • The integral is computed using numerical methods if the third argument, s, is given a numerical value.
  • The asymptotic Laplace transform can be computed using Asymptotic.
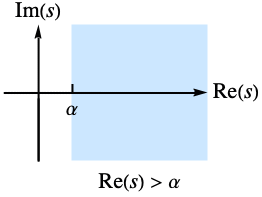
  • The Laplace transform of 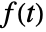exists only for complex values of s in a half-plane .
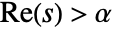  • The lower limit of the integral is effectively taken to be 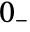, so that the Laplace transform of the Dirac delta function 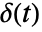is equal to 1. »
  • The following options can be given:
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    Assumptions $Assumptionsassumptions to make about parameters
    GenerateConditions Falsewhether to generate answers that involve conditions on parameters
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoalAutomaticdigits of precision sought
    PrincipalValueFalsewhether to find Cauchy principal value
    WorkingPrecisionAutomaticthe precision used in internal computations
  • Use GenerateConditions"ConvergenceRegion" to obtain the region of convergence for the Laplace transform.
  • In TraditionalForm, LaplaceTransform is output using . »

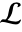Examples

open allclose all

Basic Examples  (4)

Compute the Laplace transform of a function:

Define a piecewise function:

Compute its Laplace transform:

Compute the transform at a single point:

Compute the Laplace transform of a multivariate function:

Define a multivariate piecewise function:

Compute its Laplace transform:

Scope  (67)

Basic Uses  (4)

Laplace transform of a function for a symbolic parameter s:

Laplace transforms of trigonometric functions:

Evaluate the Laplace transform for a numerical value of the parameter s:

TraditionalForm formatting:

Elementary Functions  (13)

Laplace transform of a power function:

Square root function:

Laplace transforms of polynomials:

Exponential function:

Product of an exponential and a linear function:

Expressions involving trigonometric functions:

Expressions involving hyperbolic functions:

Ratio of an exponential and a linear function:

Ratio of sine and linear functions:

Composition of elementary functions:

Logarithmic function:

Product of logarithmic and power functions:

Square of a logarithmic function:

Special Functions  (10)

Laplace transform of error and square root functions composition:

Bessel functions:

Products involving Bessel functions:

Sine integral function:

Laguerre polynomials:

Airy function:

Chebyshev polynomial:

Struve function:

Fresnel function:

Gamma function:

Hypergeometric function:

Piecewise Functions  (9)

Laplace transform of a piecewise function:

Restriction of a sine function to a half-period:

Exponential function with a left cutoff:

Triangular function:

Polynomial function with a left cutoff:

Ramp:

UnitStep:

Product of UnitStep and cosine functions:

Laplace transform of Floor:

Periodic Functions  (5)

Laplace transform of SquareWave:

TriangleWave:

SawtoothWave:

Full-wave-rectified function with period :

Rectified wave:

Generalized Functions  (5)

Laplace transform of HeavisideTheta:

DiracDelta:

Derivative of DiracDelta:

HeavisideLambda:

HeavisidePi:

Multivariate Functions  (9)

Bivariate Laplace transform of a constant:

Exponential function:

Power function:

BesselJ:

Square root:

Composition of cosine and square root:

Laplace transform of a multivariate power function:

Cosine:

Logarithm:

Formal Properties  (6)

The Laplace transform is a linear operator:

Laplace transform of is the Laplace transform of evaluated at :

Laplace transform of a first-order derivative:

Laplace transform of a second-order derivative:

Laplace transform of a product with monomials:

Laplace transform threads itself over equations:

Numerical Evaluation  (3)

Calculate the Laplace transform at a single point:

Alternatively, calculate the Laplace transform symbolically:

Then evaluate it for specific value of :

Plot the Laplace transform using numerical values only:

For some functions, the Laplace transform cannot be evaluated symbolically:

Evaluate the Laplace transform numerically and plot it:

Calculate a multivariate Laplace transform at a single point in the plane:

Fractional Calculus  (3)

Laplace transform of the MittagLefflerE functions:

ComplexPlot in the -domain:

Inverse Laplace transform to the time domain:

Laplace transform of the MittagLefflerE functions involving parameters:

Inverse Laplace transform to the time domain:

Laplace transform of the CaputoD fractional derivative:

Apply to sine function:

Compare this with the LaplaceTransform of the CaputoD derivative of the sine function:

Options  (4)

Assumptions  (1)

Specify the range for a parameter using Assumptions:

GenerateConditions  (1)

Use GenerateConditions->True to get parameter conditions for when a result is valid:

Principal Value  (1)

The Laplace transform of the following function is not defined due to the singularity at :

Use PrincipalValue to obtain the Cauchy principal value for the integral:

Working Precision  (1)

Use WorkingPrecision to obtain a result with arbitrary precision:

Applications  (12)

Ordinary Differential Equations  (5)

Solve a differential equation using Laplace transforms:

Solve for the Laplace transform:

Find the inverse transform:

Plot the solution:

Find the solution directly using DSolve:

Solve the following differential equation:

Solve for the Laplace transform:

Find the inverse transform:

Plot the solution:

Solve an RL circuit to find the current :

Verify with DSolveValue:

Green's function for an RL circuit:

Use the Green's function to solve the RL circuit:

Solve a system of ODEs:

Fractional Differential Equations  (3)

Solve a fractional-order differential equation using Laplace transforms:

Solve for the Laplace transform:

Find the inverse transform:

Plot the solution:

Find the solution directly using DSolve:

Solve the following fractional integro-differential equation:

Solve for the Laplace transform:

Find the inverse transform:

Find the solution directly using DSolve:

The following equation describes a fractional harmonic oscillator of order 1.9:

Solve for the Laplace transform:

Find the inverse transform:

Plot the solution:

Find the solution directly using DSolve:

Evaluation of Integrals  (2)

Calculate the following integral:

Compute the Laplace transform and interchange the order of Laplace transform and integration:

Perform the integration over :

Use InverseLaplaceTransform to obtain the original integral:

Verify the result:

Integral involving the Bessel function:

Perform a change of variables and introduce an auxiliary variable :

Apply the Laplace transform and interchange the order of Laplace transform and integration:

Perform the integration over :

Use InverseLaplaceTransform to obtain :

The original integral equals :

Verify the result:

Other Applications  (2)

Compute a Laplace transform using a series expansion:

The odd coefficients vanish:

The transformed series can be summed using Regularization:

Verify the result directly using LaplaceTransform:

Laplace transform of Sinc using series expansions:

Odd coefficients vanish:

Verify the result:

Properties & Relations  (3)

Use Asymptotic to compute an asymptotic approximation:

LaplaceTransform and InverseLaplaceTransform are mutual inverses:

Use NIntegrate for numerical approximation:

NIntegrate computes the transform for numeric values of the Laplace parameter s:

Possible Issues  (1)

Simplification can be required to get back the original form:

Neat Examples  (2)

LaplaceTransform done in terms of MeijerG:

Create a table of basic Laplace transforms:

Wolfram Research (1999), LaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/LaplaceTransform.html (updated 2023).

Text

Wolfram Research (1999), LaplaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/LaplaceTransform.html (updated 2023).

CMS

Wolfram Language. 1999. "LaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/LaplaceTransform.html.

APA

Wolfram Language. (1999). LaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LaplaceTransform.html

BibTeX

@misc{reference.wolfram_2024_laplacetransform, author="Wolfram Research", title="{LaplaceTransform}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/LaplaceTransform.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_laplacetransform, organization={Wolfram Research}, title={LaplaceTransform}, year={2023}, url={https://reference.wolfram.com/language/ref/LaplaceTransform.html}, note=[Accessed: 21-November-2024 ]}