UnitRootTest

UnitRootTest[data]

tests whether data came from an autoregressive time series process with unit root.

UnitRootTest[data,model,"property"]

returns the value of "property" for a given model.

Details and Options

  • UnitRootTest performs a hypothesis test on the time series data with the null hypothesis 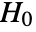that the time series satisfying an AR model has a unit root in the denominator of the corresponding transfer function and the alternative hypothesis 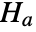that it does not.
  • Rejecting the null hypothesis allows the conclusion that the detrended data could have come from a stationary time series.
  • By default, a probability value or 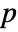-value is returned.
  • A small 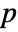-value suggests that the presence of a unit root is unlikely.
  • The data can be a list of values {x1,x2,…,xn} or a TemporalData object.
  • The model allows the specification of a model 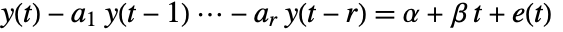, where 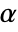is the constant offset, 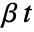is a linear drift, and 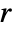is the order of the AR model.
  • The following model specifications can be used:
  • Automatic 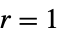and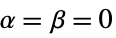
    r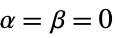
    "Constant" 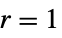and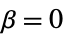
    "Drift"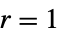
    {"Constant",r}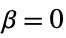
    {"Drift", r}general case
  • UnitRootTest[data] will choose Dickey–Fuller F test with 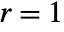and .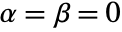
  • UnitRootTest[data,model,All] will choose all tests that apply to data and model.
  • UnitRootTest[data,model,"test"] reports the 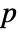-value according to "test".
  • The following tests can be used:
  • "DickeyFullerF"based on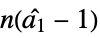
    "DickeyFullerT"based on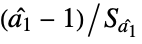
    "PhillipsPerronF"adjusted Dickey–Fuller F test
    "PhillipsPerronT"adjusted Dickey–Fuller T test
  • UnitRootTest[data,model,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • UnitRootTest[data,model,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "AllTests"list of all applicable tests
    "AutomaticTest"test chosen if Automatic is used
    "PValue"list of 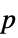-values
    "PValueTable"formatted table of 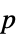-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 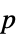-values
    "TestDataTable"formatted table of 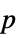-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • The following option can be used:
  • SignificanceLevel 0.05cutoff for diagnostics and reporting
  • For unit root tests, a cutoff 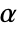is chosen such that 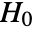is rejected only if 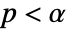. The value of 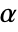used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 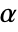is set to 0.05.

Examples

open allclose all

Basic Examples  (1)

Test whether a time series has a unit root:

The data came from a weakly stationary process:

Scope  (17)

Testing  (13)

Test time series data for a unit root:

The -values are typically large when a unit root is present:

The -values are typically small when a unit root is not present:

Test for unit root with null hypothesis that the underlying model is ARProcess[2]:

Setting the model to Automatic is equivalent to assuming an underlying ARProcess[1]:

Test for unit root, accounting for an underlying nonzero mean:

Account for a nonzero mean and assume an underlying ARProcess[3]:

Assume a nonzero mean and deterministic trend:

Assume a nonzero mean, deterministic trend, and an underlying ARProcess[3]:

Perform a particular test for unit root:

Any number of tests can be performed simultaneously:

Using Automatic applies the Dickey–Fuller F test:

The property "AutomaticTest" can be used to determine which test was chosen:

Perform all tests appropriate to the data simultaneously:

Use the property "AllTests" to identify which tests were used:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from the HypothesisTestData object:

The -value and test statistic from the "DickeyFullerT" test:

Extract any number of properties simultaneously:

The -value and test statistic from a Dickey–Fuller F test:

Reporting  (4)

Tabulate the results from a selection of tests:

A full table of all appropriate test results:

A table of selected test results:

Retrieve the entries from a test table for customized reporting:

The -values are above 0.05, so there is not enough evidence to reject at that level:

Tabulate -values for a test or group of tests:

The -value from the table:

A table of -values from all appropriate tests:

A table of -values from a subset of tests:

Report the test statistic from a test or group of tests:

The test statistic from the table:

A table of test statistics from all appropriate tests:

Options  (1)

SignificanceLevel  (1)

The significance level is used for "TestConclusion" and "ShortTestConclusion":

Applications  (3)

Maximum daily rainfall data for a 47-year period in Sydney, Australia was recorded. Of interest is whether a simple autoregressive model can model this data:

The data obviously has nonzero mean:

Choose the order of the underlying ARProcess using Schwert's rule of thumb:

There is evidence of a unit root, suggesting a simple ARProcess is not an adequate model:

Consider the annual revenue (in millions) by commercial airlines in the United States from 1937 to 1960:

The trend is confirmed using UnitRootTest:

Removing the linear trend appears to be sufficient:

Fit an ARIMAProcess to the time series:

Forecast revenue 10 years ahead using the fitted model:

Forecast index SP500:

Use a unit root test to determine trend presence:

Fit an ARIMA with nonzero integration order:

Find the forecast for the next month:

Possible Issues  (2)

The Phillips–Perron tests are limited to ARProcess[1] models:

Use Dickey–Fuller type tests to test higher orders:

UnitRootTest fails for irregularly sampled data:

Use values only:

Or set TemporalRegularity to be true:

Neat Examples  (2)

Simulate an approximation to the Dickey–Fuller T distribution for sample sizes of 100:

The test statistic and -value for the first simulated dataset:

Using the simulated distribution gives a similar result:

The approximate distributions of some test statistics under null hypothesis:

Wolfram Research (2012), UnitRootTest, Wolfram Language function, https://reference.wolfram.com/language/ref/UnitRootTest.html.

Text

Wolfram Research (2012), UnitRootTest, Wolfram Language function, https://reference.wolfram.com/language/ref/UnitRootTest.html.

CMS

Wolfram Language. 2012. "UnitRootTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnitRootTest.html.

APA

Wolfram Language. (2012). UnitRootTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnitRootTest.html

BibTeX

@misc{reference.wolfram_2024_unitroottest, author="Wolfram Research", title="{UnitRootTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/UnitRootTest.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unitroottest, organization={Wolfram Research}, title={UnitRootTest}, year={2012}, url={https://reference.wolfram.com/language/ref/UnitRootTest.html}, note=[Accessed: 22-December-2024 ]}