VandermondeMatrix[{x1,x2,…,xn}]
gives an n×n Vandermonde matrix corresponding to the nodes xi.
VandermondeMatrix[{x1,x2,…,xn},k]
gives an n×k Vandermonde matrix.
VandermondeMatrix[vmat]
converts a Vandermonde matrix vmat to a structured array.


VandermondeMatrix
VandermondeMatrix[{x1,x2,…,xn}]
gives an n×n Vandermonde matrix corresponding to the nodes xi.
VandermondeMatrix[{x1,x2,…,xn},k]
gives an n×k Vandermonde matrix.
VandermondeMatrix[vmat]
converts a Vandermonde matrix vmat to a structured array.
Details and Options



- Vandermonde matrices, when represented as structured arrays, allow for efficient storage and more efficient operations, including Det, Inverse and LinearSolve.
- Vandermonde matrices occur in computations related to polynomial interpolation and the computation of moments in the monomial basis.
- The nodes xi need not be numerical and need not be distinct.
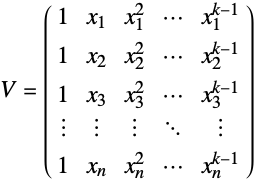
- A non-confluent Vandermonde matrix (xi distinct) has entries given by
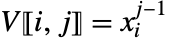 .
. - A confluent Vandermonde matrix (xi not all distinct) is the limiting form of a non-confluent Vandermonde matrix when two or more nodes are allowed to approach each other. »
- In the non-confluent case, the solution {a0,…}=LinearSolve[V,{b1,…}] gives the coefficients of the polynomial
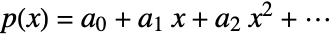 that interpolates the points {xi,bi} such that
that interpolates the points {xi,bi} such that 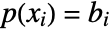 .
. - In the confluent case, the solution {a0,…}=LinearSolve[V,{b1,…}] gives the coefficients of the Hermite interpolating polynomial, where the repeated xi correspond to derivative information provided.
- Operations that are accelerated for VandermondeMatrix include:
-
Det time 
Inverse time 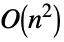
LinearSolve time 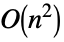
- For a VandermondeMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"Nodes" vector of nodes xi "Multiplicities" multiplicities of each unique node "Permutation" permutation list "Confluent" whether the matrix is confluent "Transposed" whether the matrix is transposed "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[VandermondeMatrix[x]] gives the Vandermonde matrix as an ordinary matrix.
- VandermondeMatrix[…,TargetStructure->struct] returns the Vandermonde matrix in the format specified by struct. Possible settings include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Structured" represent the matrix as a structured array - VandermondeMatrix[…,TargetStructureAutomatic] is equivalent to VandermondeMatrix[…,TargetStructure"Structured"].
Examples
open all close allBasic Examples (2)
Construct a Vandermonde matrix with symbolic entries:
Construct a Vandermonde matrix with numerical entries:
Get the ordinary representation of the matrix:
Solve a linear system with the matrix (a dual Vandermonde problem):
The solution gives the coefficients of an interpolating polynomial approximating the cosine:
Scope (8)
A rectangular Vandermonde matrix:
A confluent Vandermonde matrix:
A rectangular confluent Vandermonde matrix:
Represent a non-confluent Vandermonde matrix as a structured array:
The structured representation typically uses much less memory:
VandermondeMatrix objects include properties that give information about the array:
The "Nodes" property gives the vector of nodes that generates the Vandermonde matrix:
The "Permutation" property gives a permutation vector associated with the Vandermonde matrix:
The "Multiplicities" property gives the multiplicities of each unique node:
The "Confluent" property gives True if the Vandermonde matrix is confluent, and False otherwise:
The "Transposed" property gives True if the Vandermonde matrix is transposed, and False otherwise:
The "Summary" property gives a brief summary of information about the array:
The "StructuredAlgorithms" property gives a list of functions that have algorithms that use the structure of the representation:
Structured algorithms are typically faster and/or more accurate:
The exact determinant can be computed:
The value computed from VandermondeMatrix is much more accurate:
The structured algorithms may avoid problems from ill-conditioning:
Solve the linear system ![]() using VandermondeMatrix:
using VandermondeMatrix:
Solve the linear system using the normal matrix:
The residual is smaller with VandermondeMatrix:
When appropriate, structured algorithms return another structured array:
Evaluating its conjugate transpose gives a structured result:
The product with the original matrix is no longer a Vandermonde matrix:
Options (1)
Applications (7)
Generate a set of n+1 distinct samples from a function:
Use VandermondeMatrix to find a polynomial of degree n that interpolates the function at those samples:
Compare the original function and the interpolating polynomial:
Determine the coefficients of a polynomial ![]() that satisfies the interpolation conditions
that satisfies the interpolation conditions ![]() and the derivative conditions
and the derivative conditions ![]() :
:
Verify that the interpolation and derivative conditions are satisfied:
Define a set of 4 distinct points:
Fit a cubic Vandermonde polynomial to the set of points:
Columns of the inverse of the VandermondeMatrix define a set of polynomials ![]() of degree n, called Lagrange polynomials:
of degree n, called Lagrange polynomials:
Lagrange polynomials satisfy the identity ![]() :
:
Represent the Vandermonde polynomial in terms of Lagrange polynomials:
Define a polynomial with roots ![]() :
:
Construct a VandermondeMatrix from the roots:
The Frobenius companion matrix of a polynomial with known roots is similar to a diagonal matrix containing the roots, with the Vandermonde matrix acting as the similarity transformation:
The last column of the Frobenius companion matrix contains the negative of coefficients of the polynomial up to degree n-1:
These are also the same as the elementary symmetric polynomials, up to sign:
Solve for the coefficients of an n![]() -order finite difference formula:
-order finite difference formula:
Assemble the finite difference formula:
This is equivalent to the result of DifferenceQuotient:
Define a function for computing the nodes and weights of a closed Newton–Cotes rule [MathWorld]:
The trapezoidal rule is the order-1 Newton–Cotes formula:
Simpson's rule is the order-2 Newton–Cotes formula:
Boole's rule is the order-4 Newton–Cotes formula:
An n-term sum of exponential functions:
Sample the exponential function at ![]() points:
points:
Use Prony's method [Wikipedia] to recover the sum of exponentials from the data:
Properties & Relations (6)
A confluent Vandermonde matrix can be obtained as the limit of a non-confluent matrix:
Take the successive divided differences of each row:
The limit as ![]() is the confluent Vandermonde matrix:
is the confluent Vandermonde matrix:
FourierMatrix can be represented as a VandermondeMatrix:
The discriminant of a polynomial can be expressed as the square of Det of a VandermondeMatrix:
Solve a confluent Vandermonde system:
These are the coefficients of InterpolatingPolynomial with derivative values specified:
Demonstrate a factorization of the inverse of a Vandermonde matrix in terms of diagonal, Vandermonde and Hankel matrices:
Express a Cauchy matrix as a product of diagonal, Vandermonde and Hankel matrices:
Neat Examples (2)
Define a function for computing the Krylov matrix from a given matrix and vector:
Compute the eigenvalues of the matrix:
The action of a matrix exponential on a vector can be expressed in terms of a Krylov matrix and the inverse of a Vandermonde matrix:
Verify that the same result can be obtained from MatrixExp:
Verify that the same result can be obtained from DSolveValue:
Linear Caputo differential equations can also be solved in terms of a Krylov matrix and the inverse of a Vandermonde matrix, along with the Mittag–Leffler function MittagLefflerE:
Verify that the same result can be obtained from DSolveValue:
The Butcher tableau of an implicit Runge–Kutta method can be obtained by solving a primal Vandermonde system constructed from the roots of a Legendre polynomial:
Define a function for computing the implicit Runge–Kutta–Gauss coefficients to a given precision:
Use these coefficients in NDSolveValue to solve a stiff differential equation modeling flame propagation, due to Shampine:
Related Guides
Text
Wolfram Research (2022), VandermondeMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/VandermondeMatrix.html (updated 2023).
CMS
Wolfram Language. 2022. "VandermondeMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/VandermondeMatrix.html.
APA
Wolfram Language. (2022). VandermondeMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VandermondeMatrix.html
BibTeX
@misc{reference.wolfram_2025_vandermondematrix, author="Wolfram Research", title="{VandermondeMatrix}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/VandermondeMatrix.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_vandermondematrix, organization={Wolfram Research}, title={VandermondeMatrix}, year={2023}, url={https://reference.wolfram.com/language/ref/VandermondeMatrix.html}, note=[Accessed: 24-February-2026]}