VertexInDegree

VertexInDegree[g]

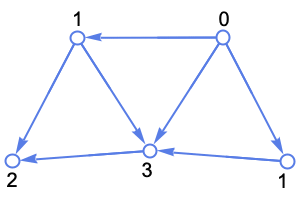
グラフ g 中のすべての頂点の頂点入次数のリストを与える．

VertexInDegree[g,v]

頂点 v の頂点入次数を与える．

VertexInDegree[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細

  • 頂点 v の頂点入次数とは v に入る有向辺の数である．
  • 無向グラフ g の辺は入辺かつ出辺であるとみなされる． »

例題

すべて開くすべて閉じる

例  (2)

各頂点の入次数を求める：

指定された頂点の入次数を求める：

スコープ  (6)

VertexInDegreeは有向グラフに使うことができる：

無向グラフ：

多重グラフ：

頂点の頂点入次数：

規則を使ってグラフを指定する：

VertexInDegreeは大きいグラフに使うことができる：

アプリケーション  (4)

CycleGraphを含む有向グラフの頂点入次数をハイライトする：

StarGraph：

GridGraph：

CompleteKaryTree：

PathGraph：

RandomGraph：

BernoulliGraphDistribution[n,p]の入次数ヒストグラムを示す：

入次数の分布はBinomialDistribution[n-1,p]に従う：

PriceGraphDistributionの頂点入次数の分布はベキ法則に従う：

動物と昆虫が何を食べるかを辺で示す食物連鎖図を作る：

入次数は捕食動物と被食動物の数に対応する：

入次数が0の種は基礎種あるいは生産者と呼ばれる：

特性と関係  (10)

無向グラフの入次数は各頂点に接続する辺の数である：

自己ループは2回数えられる：

無向グラフは各辺が入辺かつ出辺である有向グラフに相当する：

無向グラフでは，頂点入次数と出次数は頂点次数に等しい：

有向グラフでは，頂点入次数と出次数の総和が頂点次数である：

頂点次数，入次数，出次数を，頂点の前，上，下に記す：

無向グラフの全頂点の入次数の総和は辺の数の二倍である：

有向グラフの全頂点の入次数の総和は辺の数に等しい：

無向グラフの頂点入次数は隣接行列から得られる：

有向グラフの頂点入次数は隣接行列から得られる：

無向グラフの頂点の入力次数は結合行列から得ることができる：

全頂点の入次数と出次数が等しいときかつそのときに限り連結有向グラフはユークリッドグラフである：

Wolfram Research (2010), VertexInDegree, Wolfram言語関数， https://reference.wolfram.com/language/ref/VertexInDegree.html （2015年に更新）.

テキスト

Wolfram Research (2010), VertexInDegree, Wolfram言語関数， https://reference.wolfram.com/language/ref/VertexInDegree.html （2015年に更新）.

CMS

Wolfram Language. 2010. "VertexInDegree." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/VertexInDegree.html.

APA

Wolfram Language. (2010). VertexInDegree. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VertexInDegree.html

BibTeX

@misc{reference.wolfram_2024_vertexindegree, author="Wolfram Research", title="{VertexInDegree}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/VertexInDegree.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_vertexindegree, organization={Wolfram Research}, title={VertexInDegree}, year={2015}, url={https://reference.wolfram.com/language/ref/VertexInDegree.html}, note=[Accessed: 22-November-2024 ]}