BinomialDistribution[n,p]
represents a binomial distribution with n trials and success probability p.


BinomialDistribution
BinomialDistribution[n,p]
represents a binomial distribution with n trials and success probability p.
Details
- The probability for value
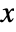 in a binomial distribution is
in a binomial distribution is 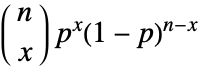 for integers from 0 to n. »
for integers from 0 to n. » - BinomialDistribution allows n to be any non-negative integer.
- BinomialDistribution allows n and p to be dimensionless quantities. »
- BinomialDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- BinomialDistribution[n,p] represents a discrete statistical distribution defined at integer values
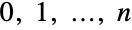 and parametrized by a non-negative real number p,
and parametrized by a non-negative real number p, 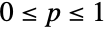 . The binomial distribution has a discrete probability density function (PDF) that is unimodal, with its peak occurring at the mean
. The binomial distribution has a discrete probability density function (PDF) that is unimodal, with its peak occurring at the mean 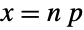 . The parameters n and p determine the height, horizontal location, and skewness of the PDF.
. The parameters n and p determine the height, horizontal location, and skewness of the PDF. - The study of the binomial distribution dates back to the early eighteenth century to the work of James Bernoulli, thus making it one of the oldest distributions to be studied. The binomial distribution is designed to model the action of flipping n (fair or unfair) coins that are independent and equal and are sampled independently and sequentially with replacement. Traditionally, p is thought of as the probability with which the experiment "succeeds", whereas
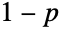 is the probability of "failure". In the coin flip analogy, the value
is the probability of "failure". In the coin flip analogy, the value 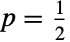 corresponds to flipping a fair coin.
corresponds to flipping a fair coin. - Despite being defined very simply, the binomial distribution serves as the basis for a number of more complicated mathematical concepts. For example, the binomial distribution can be thought of as the distribution of successes resulting from a finite n-stage Bernoulli process of having probability of success p (i.e. a discrete-time stochastic process consisting of a finite sequence of random variables, each of which is independent and identically distributed (i.i.d.) according to BernoulliDistribution[p]). Similarly, the binomial distribution is the slice distribution (SliceDistribution) of a binomial process (BinomialProcess), a discrete-time, discrete-state stochastic process consisting of a finite sequence of i.i.d. random variables following a binomial distribution, the time between which follows a geometric distribution (GeometricDistribution). Moreover, many real-world scenarios can be modeled as binomial processes, e.g. the probability of rolling a particular value among n (fair or unfair) dice. Surprising connections between the binomial distribution have also been discovered in the study of emigration patterns and in certain queueing models.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a binomial distribution. Distributed[x,BinomialDistribution[n,p]], written more concisely as xBinomialDistribution[n,p], can be used to assert that a random variable x is distributed according to a binomial distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BinomialDistribution[n,p],x] and CDF[BinomialDistribution[n,p],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a binomial distribution, EstimatedDistribution to estimate a binomial parametric distribution from given data, and FindDistributionParameters to fit data to a binomial distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic binomial distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic binomial distribution.
- TransformedDistribution can be used to represent a transformed binomial distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a binomial distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving binomial distributions.
- BinomialDistribution is related to a number of other statistical distributions. For example, BinomialDistribution[1,p] is precisely the same as BernoulliDistribution[p] on the values
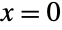 and
and 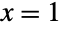 , and the sum of n independent variables distributed according to BernoulliDistribution[p] is distributed according to BinomialDistribution[n,p]. Similarly, BinomialDistribution[t,p] has the same PDF as BinomialProcess[p][t], a property due to the fact that BinomialDistribution[t,p] is precisely SliceDistribution[BinomialProcess[p],t]. BinomialDistribution[n,p] is also the limiting distribution for several distributions. In particular, BinomialDistribution[n,p] converges to NormalDistribution[μ,σ] for fixed p as n tends to Infinity where
, and the sum of n independent variables distributed according to BernoulliDistribution[p] is distributed according to BinomialDistribution[n,p]. Similarly, BinomialDistribution[t,p] has the same PDF as BinomialProcess[p][t], a property due to the fact that BinomialDistribution[t,p] is precisely SliceDistribution[BinomialProcess[p],t]. BinomialDistribution[n,p] is also the limiting distribution for several distributions. In particular, BinomialDistribution[n,p] converges to NormalDistribution[μ,σ] for fixed p as n tends to Infinity where 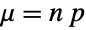 and
and 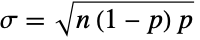 and converges to a discretized PoissonDistribution[p] as n tends to Infinity and p tends to 0, while HypergeometricDistribution[n,p] limits to BinomialDistribution[n,p] as p tends to Infinity. BinomialDistribution is a two-variable case of MultinomialDistribution, is a constituent piece of BetaBinomialDistribution, and has a natural relationship with NegativeBinomialDistribution.
and converges to a discretized PoissonDistribution[p] as n tends to Infinity and p tends to 0, while HypergeometricDistribution[n,p] limits to BinomialDistribution[n,p] as p tends to Infinity. BinomialDistribution is a two-variable case of MultinomialDistribution, is a constituent piece of BetaBinomialDistribution, and has a natural relationship with NegativeBinomialDistribution.
Examples
open all close allBasic Examples (3)
Scope (8)
Generate a sample of pseudorandom numbers from a binomial distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
The distribution is symmetric for ![]() :
:
The distribution becomes symmetric for large n:
The limiting value is the value of kurtosis of the standard NormalDistribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Use dimensionless Quantity to define BinomialDistribution:
Applications (12)
CDF of BinomialDistribution is an example of a right-continuous function:
A basketball player has a free-throw percentage of 0.75. Simulate 10 free throws:
Find the probability that the player hits 2 out of 3 free throws in a game:
Find the probability that the player hits the last 2 of 5 free throws:
Find the expected number of hits in a game with n free throws:
A baseball player is a 0.300 hitter. Simulate 5 at bats:
Find the expected number of hits if the player comes to bat 3 times:
A drug has proven to be effective in 30% of cases. Find the probability it is effective in at least 3 of 4 patients:
Find the expected number of successes when applied to 500 cases:
The number of heads in n flips with a fair coin can be modeled with BinomialDistribution:
Show the distribution of heads for 100 coin flips:
Compute the probability that there are between 60 and 80 heads in 100 coin flips:
Now, suppose that for an unfair coin the probability of heads is 0.6:
The distribution and the corresponding probabilities have changed:
A machine produces parts, with 1 in 10 defective:
Compute the probability that at most 1 of 5 parts is defective:
An airplane engine fails with probability p; compute the probability that no more than 2 of 4 fail:
Compute the probability that no more than 1 of 2 fails:
Decide when the choice of four engines is better than two engines:
A system uses triple redundancy with three microprocessors and is designed to operate as long as one processor is still functional. The probability that a microprocessor is still functional after ![]() seconds is
seconds is ![]() . Find the probability that the system is still operating after
. Find the probability that the system is still operating after ![]() seconds:
seconds:
With mean time to failure for each processor ![]() , find out when the system functions with a probability of less than 99%:
, find out when the system functions with a probability of less than 99%:
Gary Kasparov, chess champion, plays in a tournament simultaneously against 100 amateurs. It has been estimated that he loses about 1% of such games. Find the probability of losing 0, 2, 5, and 10 games:
Use a Poisson approximation to compute the same probabilities:
Perform the same computation when he is playing 5 games, but with stronger opposition so that his loss probability is 10% instead:
In this case the Poisson approximation is less accurate:
A packet consisting of a string of n symbols is transmitted over a noisy channel. Each symbol has probability ![]() of incorrect transmission. Find n such that the probability of incorrect packet transmission is less than
of incorrect transmission. Find n such that the probability of incorrect packet transmission is less than ![]() :
:
Compute the same limit using a Poisson approximation:
Find the probability that ![]() out of n customers need a service if each uses it with probability p:
out of n customers need a service if each uses it with probability p:
Compute the probability that more than ![]() (capacity) simultaneous service requests are made:
(capacity) simultaneous service requests are made:
Compute the probability of getting service if ![]() and
and ![]() for different capacities
for different capacities ![]() :
:
Find the smallest capacity ![]() that provides a 99.9% probability of getting service:
that provides a 99.9% probability of getting service:
Two players roll dice. If the total of both numbers is less than 10, the second player is paid 4 cents; otherwise the first player is paid 9 cents. Is the game fair?:
The game is not fair, since mean scores per game are not equal:
Find the probability that after n games the player at the disadvantage scores more:
Properties & Relations (9)
Binomial distribution is closed under addition:
BinomialDistribution[n,p] converges to a normal distribution as ![]() :
:
Relationships to other distributions:
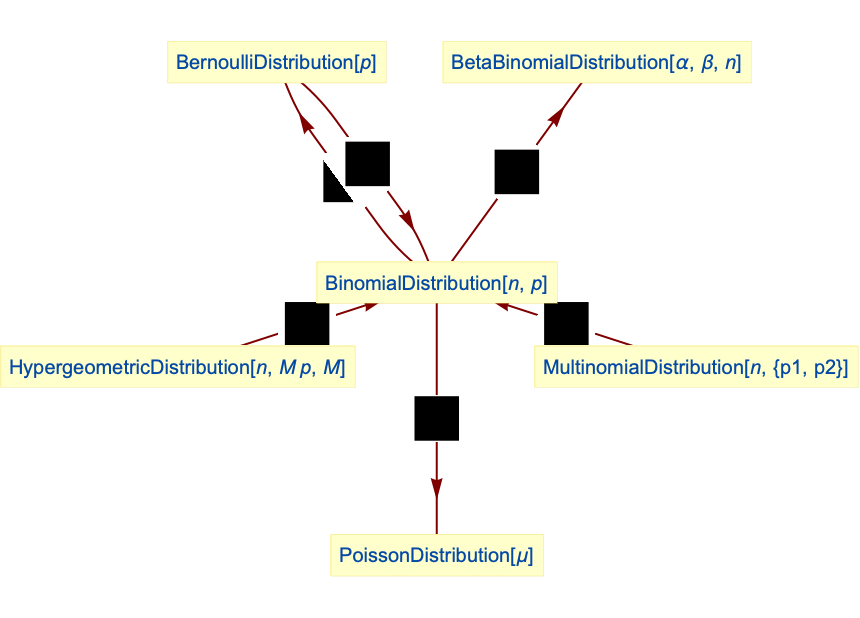
BinomialDistribution with ![]() is equivalent to BernoulliDistribution:
is equivalent to BernoulliDistribution:
The sum of n independent variables with BernoulliDistribution is binomial distributed:
BinomialDistribution is the infinite population limit of HypergeometricDistribution:
BinomialDistribution approaches the PoissonDistribution for large n and small p:
A marginal of bivariate multinomial distribution is a binomial distribution:
Confirm by comparing probability mass functions:
BetaBinomialDistribution is a mixture of BinomialDistribution and BetaDistribution:
Possible Issues (3)
BinomialDistribution is not defined when p is not between zero and one:
BinomialDistribution is not defined when n is not a positive integer:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Text
Wolfram Research (2007), BinomialDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BinomialDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "BinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BinomialDistribution.html.
APA
Wolfram Language. (2007). BinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinomialDistribution.html
BibTeX
@misc{reference.wolfram_2025_binomialdistribution, author="Wolfram Research", title="{BinomialDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BinomialDistribution.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_binomialdistribution, organization={Wolfram Research}, title={BinomialDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BinomialDistribution.html}, note=[Accessed: 09-March-2026]}