WarpingDistance
WarpingDistance[s1,s2]
列 s1と s2の間の動的タイムワーピング(DTW)距離を与える.
WarpingDistance[s1,s2,win]
局所探索に win で指定された窓を使う.
詳細とオプション



- WarpingDistanceは参照列 s1とクエリ列 s2の任意の対応関係の最短距離を与える.
- 距離は
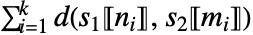 で与えられる.s1〚ni〛と s2〚mi〛は対応する要素である.
で与えられる.s1〚ni〛と s2〚mi〛は対応する要素である. - WarpingCorrespondenceを使って実質的な対応を計算する.
- 列 siは,数値,ブールスカラーあるいはベクトルのリストでよい.
- 探索窓 win の可能な設定
-

Automatic 完全探索 
r 半径 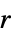 の斜め帯窓
の斜め帯窓
{"SlantedBand",r} 半径 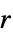 の斜め帯窓
の斜め帯窓
{"Band",r} 半径 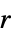 の帯窓 (Sakoe-Chiba)
の帯窓 (Sakoe-Chiba)
{"Parallelogram",a} 傾斜 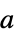 と
と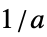 で原点に置かれた平行四辺形窓(板倉)
で原点に置かれた平行四辺形窓(板倉) 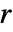 を小さくすると計算は速くなるが結果の最適度は劣るようになる.
を小さくすると計算は速くなるが結果の最適度は劣るようになる.![max(Length[s_1],Length[s_2])<=2 r +1 max(Length[s_1],Length[s_2])<=2 r +1](Files/WarpingDistance.ja/13.png) の場合は,
の場合は,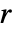 は影響しない.
は影響しない.- サポートされるオプション
-
DistanceFunction Automatic 使用する距離関数 Method Automatic 使用する動的タイムワーピングの異形 - WarpingDistanceはDistanceFunctiond オプションを次の設定で使うことができる.
-
Automatic 距離関数を自動的に決定する EuclideanDistance ユークリッド距離 ManhattanDistance マンハッタン(「都市ブロック」)距離 BinaryDistance 要素が等しい場合は0,それ以外は1 ChessboardDistance チェビシェフ(上限ノルム)距離 SquaredEuclideanDistance ユークリッド距離の二乗 NormalizedSquaredEuclideanDistance ユークリッド距離の二乗の正規化 CosineDistance 角余弦距離 CorrelationDistance 相関係数距離 BrayCurtisDistance Total[Abs[u-v]]/Total[Abs[u+v]] CanberraDistance Total[Abs[u-v]/(Abs[u]+Abs[v])] MatchingDissimilarity ブールベクトル間のマッチング非類似度 - デフォルトで,次の距離関数が使われる.
-
EuclideanDistance 数値データ MatchingDissimilarity ブール型データ - Method->Automaticを使うと,s2の全要素が s1の全要素とマッチされる.
- Method->{"MatchingInterval"match}を使うと,s2を s1の部分列とマッチすることができる.次は match の可能な設定である.
-
Automatic 完全なマッチ "Flexible" 両端で柔軟 "FlexibleEnd" 区間の終端でのみ柔軟
例題
すべて開くすべて閉じるスコープ (10)
データ (7)
一般化と拡張 (1)
オプション (6)
DistanceFunction (5)
ブール列の場合,WarpingDistanceはMatchingDissimilarityを使う:
一次元信号の場合,NormalizedSquaredEuclideanDistanceとCorrelationDistanceは常に0を返す:
アプリケーション (6)
ヨーロッパ連合諸国の首都で昨年の気温シカゴに最もよく似ている都市を求める.WarpingDistanceを使って気温列間の類似度を決定する:
ヨーロッパ連合のすべての首都について,気温時系列間のペアごとの距離を計算する:
特性と関係 (8)
WarpingDistanceは,対応する要素間のすべての距離の合計を与える:
しかし,短い半径を使うとアライメントの最適さ加減が低下し,結果として距離の値が大きくなる:
WarpingDistanceは対称関数である:
テキスト
Wolfram Research (2016), WarpingDistance, Wolfram言語関数, https://reference.wolfram.com/language/ref/WarpingDistance.html.
CMS
Wolfram Language. 2016. "WarpingDistance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WarpingDistance.html.
APA
Wolfram Language. (2016). WarpingDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WarpingDistance.html