CentralFeature

CentralFeature[{x1,x2,…}]

gives the central feature of the elements .

CentralFeature[{x1v1,x2v2,…}]

gives the vi corresponding to the central feature .

CentralFeature[data]

gives the central feature for several different forms of data.

Details and Options

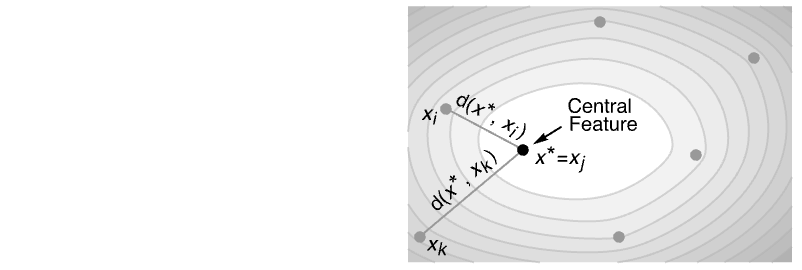
  • CentralFeature is a location measure. It gives a point in the data with the minimum total distance to every other point.
  • CentralFeature finds the element 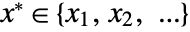that minimizes the sum of distances 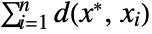for the unweighted case and 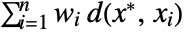for the weighted case.
  • The data data has the following forms and interpretations:
  • {data1,data2,…}list of data of different formats including numerical, geospatial, textual, visual, dates and times, as well as combinations of these
    {data1,data2,…}{v1,v2,…}data with indices {v1,v2,…}
    {data1,data2,…}Automatictake the vi to be successive integers i
    GeoPosition[…]array of geodetic positions
    WeightedData[…]data with weights
  • The following option can be given:
  • DistanceFunction Automaticthe distance metric to use
  • The setting for DistanceFunction can be any distance or dissimilarity function or a function f defining a distance between two points.
  • By default, the following distance functions are used for different types of elements:
  • EuclideanDistancenumeric data
    ImageDistanceimages
    JaccardDissimilarityBoolean data
    EditDistancetext and nominal sequences
    Abs[DateDifference[#1,#2]]&dates and times
    ColorDistancecolors
    GeoDistancegeospatial data
    Boole[SameQ[#1,#2]]&nominal data
    HammingDistancenominal vector data
    WarpingDistancenumerical sequences
  • All images are first conformed using ConformImages when the option DistanceFunction is Automatic.
  • By default, when data elements are mixed-type vectors, distances are computed independently for each type and combined using Norm.

Examples

open allclose all

Basic Examples  (2)

Find the central feature in a list of vectors:

Find the central feature in a list of vectors with given weights:

Scope  (9)

Same inputs with different output formats:

Central feature works with WeightedData:

Central feature of a large array:

Weighted central feature:

Find the central feature of data involving quantities:

Find the central feature of a list of images:

List of pictures:

List of 3D images:

Compute the central feature of strings:

Compute the central feature of Boolean vectors:

Compute the central feature of a list of date objects:

Compute the central feature of geodetic positions:

Options  (2)

DistanceFunction  (2)

By default, Euclidean distance is used:

The ChessboardDistance only takes into account the dimension with the largest separation:

The DistanceFunction can be given as a symbol:

Or as a pure function:

Applications  (4)

Obtain a robust estimate of multivariate location when outliers are present:

Extreme values have a large influence on the Mean:

Sample points from a convex polygon:

Estimate the center of the polygon by computing the central feature of random points:

Find the central feature of California, based on the location of cities:

Find the central feature of California, based on the location of cities weighted by population:

Draw the cities' locations (gray), unweighted central feature (red) and weighted central feature (black):

The top eight largest cities in Ohio:

The central feature of the eight cities based on TravelDistance:

The sum of distances from the central feature to the other cities, based on TravelDistance:

Draw the cities' locations (gray) and the central feature (red):

Properties & Relations  (5)

CentralFeature is a multivariate location measure:

Mean is also a location measure:

Visualize the data points with central feature and mean:

CentralFeature finds a point belonging to the data that minimizes the sum of distances:

Compute the central feature directly from the definition:

Visualize the sum of distances function together with the data points:

CentralFeature is the same as Median with univariate data when the data length is odd:

CentralFeature finds an element in the data that minimizes the sum of distances to other data points:

SpatialMedian finds a point in the domain that minimizes the sum of distances:

The sum of distances with respect to CentralFeature is greater than or equal to the one with respect to SpatialMedian:

Create a random graph with edge weights sampled uniformly between 0 and 1:

Locate the GraphCenter:

Specify the distance between each pair of vertices using GraphDistance:

Locate the center using CentralFeature:

Possible Issues  (1)

CentralFeature of a non-weighted, two-element list returns the first element:

For weighted two-element lists, it chooses the element with the highest weight, which trivially minimizes :

Wolfram Research (2017), CentralFeature, Wolfram Language function, https://reference.wolfram.com/language/ref/CentralFeature.html.

Text

Wolfram Research (2017), CentralFeature, Wolfram Language function, https://reference.wolfram.com/language/ref/CentralFeature.html.

CMS

Wolfram Language. 2017. "CentralFeature." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CentralFeature.html.

APA

Wolfram Language. (2017). CentralFeature. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralFeature.html

BibTeX

@misc{reference.wolfram_2024_centralfeature, author="Wolfram Research", title="{CentralFeature}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/CentralFeature.html}", note=[Accessed: 26-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_centralfeature, organization={Wolfram Research}, title={CentralFeature}, year={2017}, url={https://reference.wolfram.com/language/ref/CentralFeature.html}, note=[Accessed: 26-April-2024 ]}