WavePDEComponent

WavePDEComponent[vars,pars]

yields a wave equation PDE term with model variables vars and model parameters pars.

Details

  • WavePDEComponent returns a sum of differential operators to be used as a part of partial differential equations
  • WavePDEComponent can be used to model wave equations with dependent variable 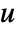, independent variables 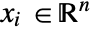and time variable .
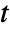  • Time-dependent model variables vars are vars={u[t,x1,…,xn],t,{x1,…,xn}}.
  • The WavePDEComponent is based on a diffusion term:

    • (partialu^2)/(partialt^2)- del .(c^2 del u(x))^(︷^( diffusion term ))

  • The wave PDE term 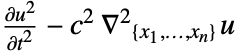is realized as a DiffusionPDETerm with 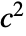as a diffusion coefficient, for a constant resulting in .
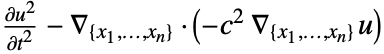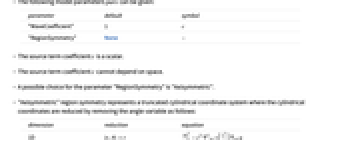
  • The following model parameters pars can be given:
  • parameterdefaultsymbol
    "WaveCoefficient"1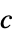
    "RegionSymmetry"None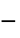
  • The source term coefficient 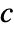is a scalar.
  • The source term coefficient 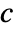cannot depend on space.
  • A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
  • "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
  • dimensionreductionequation
    1D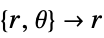
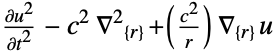
    2D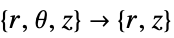
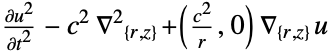
  • If the WavePDEComponent depends on parameters 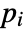that are specified in the association pars as …,keypi…,pivi,…, the parameters 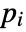are replaced with .

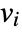Examples

open allclose all

Basic Examples  (3)

Define a wave PDE component:

Activate the component:

Define a wave PDE component with a symbolic coefficient:

Find the eigenvalues of a wave equation:

Scope  (1)

Define a 2D axisymmetric wave PDE component:

Activate the term:

Wolfram Research (2020), WavePDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/WavePDEComponent.html (updated 2022).

Text

Wolfram Research (2020), WavePDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/WavePDEComponent.html (updated 2022).

CMS

Wolfram Language. 2020. "WavePDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/WavePDEComponent.html.

APA

Wolfram Language. (2020). WavePDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WavePDEComponent.html

BibTeX

@misc{reference.wolfram_2025_wavepdecomponent, author="Wolfram Research", title="{WavePDEComponent}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/WavePDEComponent.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_wavepdecomponent, organization={Wolfram Research}, title={WavePDEComponent}, year={2022}, url={https://reference.wolfram.com/language/ref/WavePDEComponent.html}, note=[Accessed: 22-February-2025 ]}