WavePDEComponent

WavePDEComponent[vars,pars]

波動方程式のPDE項 を，モデル変数 vars とモデルパラメータ pars で与える．

詳細

  • WavePDEComponentは，偏微分方程式の一部として使われる微分演算子の和を返す．
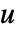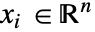  • WavePDEComponentを使って，従属変数 ，独立変数 ，時間変数 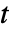で波動方程式がモデル化できる．
  • 時間依存モデル変数 vars は vars={u[t,x1,…,xn],t,{x1,…,xn}}である．
  • WavePDEComponentは拡散項に基づいている．

    • (partialu^2)/(partialt^2)- del .(c^2 del u(x))^(︷^( diffusion term ))

  • 波動方程式のPDE項 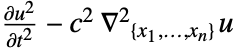は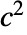，を拡散係数とするDiffusionPDETermとして実現される．定数についての結果は 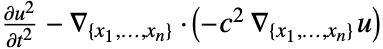である．
  • 次のモデルパラメータ pars を使うことができる．
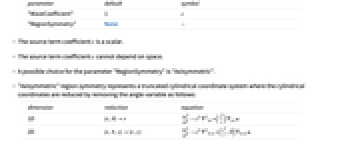
  • パラメータデフォルトシンボル
    "WaveCoefficient"1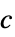
    "RegionSymmetry"None
  • ソース項係数 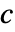はスカラーである．
  • ソース項係数 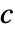は空間に依存することはできない．
  • パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある．
  • "Axisymmetric"領域対称性は，以下のように角変数を削除することで円筒座標が削減された切頂円筒座標系を表す．
  • 次元削減方程式
    1D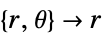
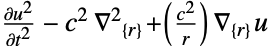
    2D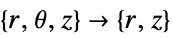
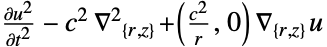
  • WavePDEComponentが連想 pars で…,keypi…,pivi,…として指定されるパラメータ 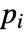に依存するなら，パラメータ 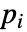は 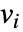で置換される．

例題

すべて開くすべて閉じる

例  (3)

波動方程式のPDE成分を定義する：

成分をアクティブにする：

波動方程式のPDE成分を記号係数で定義する：

波動方程式の固有値を求める：

スコープ  (1)

2D軸対称波動偏微分方程式の成分を定義する：

項をActivateする：

Wolfram Research (2020), WavePDEComponent, Wolfram言語関数， https://reference.wolfram.com/language/ref/WavePDEComponent.html （2022年に更新）.

テキスト

Wolfram Research (2020), WavePDEComponent, Wolfram言語関数， https://reference.wolfram.com/language/ref/WavePDEComponent.html （2022年に更新）.

CMS

Wolfram Language. 2020. "WavePDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/WavePDEComponent.html.

APA

Wolfram Language. (2020). WavePDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WavePDEComponent.html

BibTeX

@misc{reference.wolfram_2024_wavepdecomponent, author="Wolfram Research", title="{WavePDEComponent}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/WavePDEComponent.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_wavepdecomponent, organization={Wolfram Research}, title={WavePDEComponent}, year={2022}, url={https://reference.wolfram.com/language/ref/WavePDEComponent.html}, note=[Accessed: 18-November-2024 ]}