WaveletFilterCoefficients

WaveletFilterCoefficients[wave,filt]

タイプ filt の記号ウェーブレット wave のフィルタ係数を与える．

詳細とオプション

  • WaveletFilterCoefficients[wave,filt]は{{n,cn},{n+1,cn+1},…}の形式のリストを返す．ただし，n は指標，cn は対応するフィルタ係数である．
  • 直交ウェーブレットで使用可能なフィルタ filt には"PrimalLowpass"と"PrimalHighpass"がある．
  • 主ハイパスフィルタ係数は 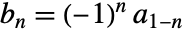を満足する．ただし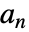， は主ローパスフィルタ係数である．
  • スケーリング関数 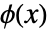とウェーブレット関数 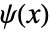は以下の関係を満足する．
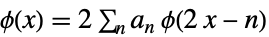
  • （主）スケーリング細分化方程式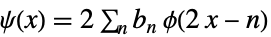
    （主）ウェーブレット細分化方程式
  • 双直交ウェーブレットの場合，使用可能なフィルタ filt には，"PrimalLowpass"，"PrimalHighpass"，"DualLowpass"，"DualHighpass"がある．
  • 主ハイパスフィルタ係数は 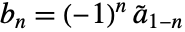を満足する．ただし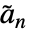，は双対ローパスフィルタ係数である．双対ハイパスフィルタ係数は 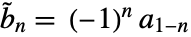を満足する．ただし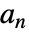， は主ローパスフィルタ係数である．
  • 主スケーリング関数 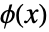とウェーブレット関数 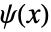は次の関係を満足する．
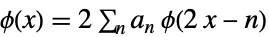
  • （主）スケーリング細分化方程式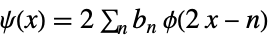
    （主）ウェーブレット細分化方程式
  • 双対スケーリング関数 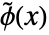と双対ウェーブレット関数 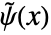は以下を満足する．
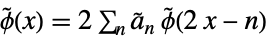
  • （双対）スケーリング細分化方程式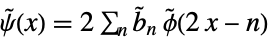
    （双対）ウェーブレット細分化方程式
  • コンパクトサポートの離散ウェーブレットの場合はLiftingWaveletTransformやコンパイルされたスタンドアロンのウェーブレット変換コード生成に使われるLiftingFilterDataオブジェクトを作ることもできる．次の filt 値を使うことができる．
  • "LiftingFilter"デフォルトリフティングフィルタ
    "AllLiftingFilter"可能なすべてのリフティングフィルタ
    "BestLiftingFilter"最も安定したリフティングフィルタ
  • WorkingPrecision->prec とオプションを設定すると，フィルタ係数は精度 prec で計算される．デフォルトでWorkingPrecision->MachinePrecisionが使われる．

例題

すべて開くすべて閉じる

例  (4)

主ローパスフィルタ係数：

主ハイパスフィルタ係数：

双対ローパスフィルタ係数：

双対ハイパスフィルタ係数：

スコープ  (5)

主ローパスフィルタ係数を計算する：

主ハイパスフィルタ係数：

双対ローパスフィルタ係数：

双対ハイパスフィルタ係数：

"Properties"は使用可能な特性のリストを返す：

BiorthogonalSplineWaveletの特性：

オプション  (2)

WorkingPrecision  (2)

デフォルトで，WorkingPrecision->MachinePrecisionが使われる：

より精度の高いフィルタ計算を使う：

特性と関係  (3)

ローパスフィルタ係数の総和は単位元になる．：

ハイパスフィルタ係数の総和は0になる．：

ローパスフィルタ係数とハイパスフィルタ係数は直交する．：

Wolfram Research (2010), WaveletFilterCoefficients, Wolfram言語関数， https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

テキスト

Wolfram Research (2010), WaveletFilterCoefficients, Wolfram言語関数， https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

CMS

Wolfram Language. 2010. "WaveletFilterCoefficients." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

APA

Wolfram Language. (2010). WaveletFilterCoefficients. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html

BibTeX

@misc{reference.wolfram_2024_waveletfiltercoefficients, author="Wolfram Research", title="{WaveletFilterCoefficients}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_waveletfiltercoefficients, organization={Wolfram Research}, title={WaveletFilterCoefficients}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html}, note=[Accessed: 22-November-2024 ]}