WOLFRAM

Wolfram 语言与系统参考资料中心

WaveletFilterCoefficients[wave,filt]

给出类型为 filt 的符号小波 wave 的滤波器系数.

更多信息和选项
Details and Options Details and Options
范例  
基本范例  
范围  
选项  
WorkingPrecision  
属性和关系  
参见
相关指南
历史
按以下格式引用：

WaveletFilterCoefficients

WaveletFilterCoefficients[wave,filt]

给出类型为 filt 的符号小波 wave 的滤波器系数.

更多信息和选项

  • WaveletFilterCoefficients[wave,filt] 给出形如 {{n,cn},{n+1,cn+1},…} 的列表，其中 n 是指标，而 cn 是相应的滤波器系数.
  • 对于正交小波，可能的滤波器 filt 包括："PrimalLowpass" 和 "PrimalHighpass".
  • 原高通滤波器系数满足 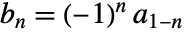，其中 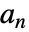是原低通滤波器系数.
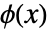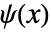  • 尺度函数 和小波函数 满足关系：
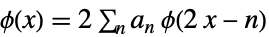
  • （原）尺度修正方程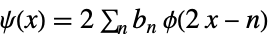
    （原）小波修正方程
  • 对于双正交小波，可能的滤波器 filt 包括："PrimalLowpass"、"PrimalHighpass"、"DualLowpass" 和"DualHighpass".
  • 原高通滤波器系数满足 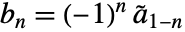，其中 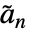是对偶低通滤波器系数. 对偶高通滤波器系数满足 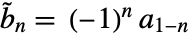，其中 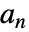是原低通滤波器系数.
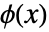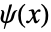  • 原尺度函数 和小波函数 满足关系：
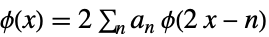
  • （原）尺度修正方程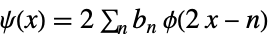
    （原）小波修正方程
  • 对偶尺度函数 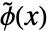和对偶小波函数 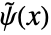满足：
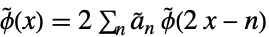
  • （对偶）尺度修正方程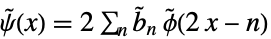
    （对偶）小波修正方程
  • 对于具有紧支集的离散小波，可以产生用于 LiftingWaveletTransform 的 LiftingFilterData 对象，也可以生成已编译的独立小波变换代码. 可以使用下列 filt 值：
  • "LiftingFilter"默认的提升滤波器
    "AllLiftingFilter"所有可能的提升滤波器
    "BestLiftingFilter"最稳定的提升滤波器
  • 在选项设置 WorkingPrecision->prec 下，滤波器系数使用精度 prec 计算. 默认情况下，使用WorkingPrecision->MachinePrecision.

范例

打开所有单元 关闭所有单元

基本范例  (4)

原低通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[HaarWavelet[], WorkingPrecision -> ∞]

原高通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[HaarWavelet[], "PrimalHighpass", WorkingPrecision -> ∞]

对偶低通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[BiorthogonalSplineWavelet[2, 2], "DualLowpass", WorkingPrecision -> ∞]

对偶高通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[BiorthogonalSplineWavelet[2, 2], "DualHighpass", WorkingPrecision -> ∞]

范围  (5)

计算原低通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[DaubechiesWavelet[2], "PrimalLowpass"]

原高通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[DaubechiesWavelet[2], "PrimalHighpass"]

对偶低通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[BiorthogonalSplineWavelet[2, 4], "DualLowpass"]

对偶高通滤波器系数：

Wolfram Language code: WaveletFilterCoefficients[BiorthogonalSplineWavelet[2, 4], "DualHighpass"]

"Properties" 给出可用属性的一个列表：

Wolfram Language code: WaveletFilterCoefficients[DaubechiesWavelet[2], "Properties"]

BiorthogonalSplineWavelet 的属性：

Wolfram Language code: WaveletFilterCoefficients[BiorthogonalSplineWavelet[2, 2], "Properties"]

选项  (2)

WorkingPrecision  (2)

默认情况下，使用 WorkingPrecision->MachinePrecision：

Wolfram Language code: filt1 = WaveletFilterCoefficients[DaubechiesWavelet[4]]
Wolfram Language code: filt2 = WaveletFilterCoefficients[DaubechiesWavelet[4], WorkingPrecision -> MachinePrecision]
Wolfram Language code: filt1 == filt2

使用高精度滤波器计算：

Wolfram Language code: WaveletFilterCoefficients[DaubechiesWavelet[4], WorkingPrecision -> 20]
Wolfram Language code: Precision[%]
Wolfram Language code: WaveletFilterCoefficients[BiorthogonalSplineWavelet[4, 4], WorkingPrecision -> ∞]
Wolfram Language code: Precision[%]

属性和关系  (3)

低通滤波器系数的和为1；：

Wolfram Language code: WaveletFilterCoefficients[DaubechiesWavelet[3], "PrimalLowpass"][[All, 2]]//Total//Chop

高通滤波器系数的和为0；：

Wolfram Language code: WaveletFilterCoefficients[DaubechiesWavelet[3], "PrimalHighpass"][[All, 2]]//Total//Chop

低通和高通滤波器系数是正交的；：

Wolfram Language code: WaveletFilterCoefficients[HaarWavelet[]][[All, 2]].WaveletFilterCoefficients[HaarWavelet[], "PrimalHighpass"][[All, 2]]
Wolfram Research (2010)，WaveletFilterCoefficients，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

文本

Wolfram Research (2010)，WaveletFilterCoefficients，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

CMS

Wolfram 语言. 2010. "WaveletFilterCoefficients." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

APA

Wolfram 语言. (2010). WaveletFilterCoefficients. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html 年

BibTeX

@misc{reference.wolfram_2026_waveletfiltercoefficients, author="Wolfram Research", title="{WaveletFilterCoefficients}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html}", note=[Accessed: 22-June-2026]}

BibLaTeX

@online{reference.wolfram_2026_waveletfiltercoefficients, organization={Wolfram Research}, title={WaveletFilterCoefficients}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html}, note=[Accessed: 22-June-2026]}