WienerProcess[μ,σ]
表示 drift 为 μ、波动率为 σ 的 Wiener 过程.
表示 drift 为 0、波动率为 1 的标准 Wiener 过程.


WienerProcess
WienerProcess[μ,σ]
表示 drift 为 μ、波动率为 σ 的 Wiener 过程.
表示 drift 为 0、波动率为 1 的标准 Wiener 过程.
更多信息
- WienerProcess 也称为布朗运动、连续时间随机游走或者集成高斯白噪声.
- WienerProcess 是一个连续时间和连续状态随机过程.
- 时间 t 处的状态服从 NormalDistribution[μ t,σ
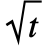 ].
]. - 参数 μ 可以是任意实数,并且参数 σ 可以是任意正实数.
- WienerProcess 可以与诸如 Mean、PDF、Probability 和 RandomFunction 一起使用.
范例
打开所有单元 关闭所有单元范围 (12)
过程切片属性 (5)
单变量 SliceDistribution:
二阶 PDF:
高阶 PDF:
CentralMoment 和它的母函数:
FactorialMoment 没有符号式阶数的解析式:
Cumulant 和它的母函数:
应用 (7)
使用二次 WienerProcess 定义 martingale 过程:
直接使用 WienerProcess 来模拟 GeometricBrownianMotionProcess:
与相应的 GeometricBrownianMotionProcess 比较:
直接使用 WienerProcess 来模拟 BrownianBridgeProcess:
与相应的 BrownianBridgeProcess 比较:
求具有正偏移的 WienerProcess 浮动到 2 所花的时间分布:
对数据拟合 InverseGaussianDistribution:
属性和关系 (12)
Wiener 过程的相关函数与 RandomWalkProcess 的相同:
Wiener 过程是一个特殊 ItoProcess:
模拟标准 WienerProcess 的正侧所花的时间比率:
在极限下,比率服从 ArcSinDistribution:
求在时间0和1之间 WienerProcess 最后改变符号的分布:
在极限下,次数服从 ArcSinDistribution:
求对应于 WienerProcess 最大值的时间分布,直至时间 1:
在极限下,次数服从 ArcSinDistribution:
与 WienerProcess 比较:
与 WienerProcess 比较:
GeometricBrownianMotionProcess 是 WienerProcess 的变换:
与相应 GeometricBrownianMotionProcess 的切片分布比较:
Wiener 过程是 BrownianBridgeProcess 的变换:
文本
Wolfram Research (2012),WienerProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/WienerProcess.html.
CMS
Wolfram 语言. 2012. "WienerProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WienerProcess.html.
APA
Wolfram 语言. (2012). WienerProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WienerProcess.html 年
BibTeX
@misc{reference.wolfram_2025_wienerprocess, author="Wolfram Research", title="{WienerProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/WienerProcess.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_wienerprocess, organization={Wolfram Research}, title={WienerProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/WienerProcess.html}, note=[Accessed: 05-March-2026]}