InverseGaussianDistribution

✖
`InverseGaussianDistribution`

✖

InverseGaussianDistribution[μ,λ]

represents an inverse Gaussian distribution with mean μ and scale parameter λ.

✖

InverseGaussianDistribution[μ,λ,θ]

represents a generalized inverse Gaussian distribution with parameters μ, λ, and θ.

Details

InverseGaussianDistribution[μ,λ] is also known as the inverse normal or Wald distribution.
InverseGaussianDistribution[μ,λ,θ] is also known as the Sichel distribution.
The probability density for value 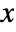in an inverse Gaussian distribution is proportional to 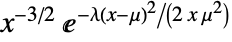for 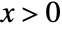, and zero for . »
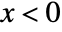The probability density for value 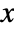in a generalized inverse Gaussian distribution is proportional to 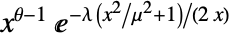for 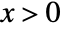, and zero for .
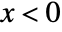InverseGaussianDistribution allows μ and λ to be any positive real numbers and θ to be any real number.
InverseGaussianDistribution allows λ and μ to be any quantities of the same unit dimensions, and θ to be a dimensionless quantity. »
InverseGaussianDistribution can be used with such functions as Mean, CDF, and RandomVariate. »

Background & Context

InverseGaussianDistribution[μ,λ,θ] represents a continuous statistical distribution defined over the interval 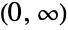and parametrized by a real number θ (called an "index parameter") and by two positive real numbers μ (the mean of the distribution) and λ (called a "scale parameter"). Overall, the probability density function (PDF) of an inverse Gaussian distribution is unimodal with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and its concentration near the 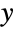axis) is determined by the values of μ, λ, and θ. In addition, the tails of the PDF are "thin" in the sense that the PDF decreases exponentially rather than algebraically for large values of 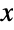. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The three-parameter version is sometimes referred to as the generalized inverse Gaussian distribution or the Sichel distribution, while the two-parameter form InverseGaussianDistribution[μ,λ] (which is equivalent to InverseGaussianDistribution[μ,λ,-1/2]) is most often referred to as "the" inverse Gaussian distribution, though it is also sometimes referred to as Wald's distribution.
Unlike the "inverse" relationships held between several other pairs of probability distributions (e.g. InverseGammaDistribution being inverse to GammaDistribution and InverseChiSquareDistribution being inverse to ChiSquareDistribution), and characterized by the behavior of certain reciprocals of random variables, InverseGaussianDistribution is not the distribution followed by the reciprocal 1/X of a normally distributed (or Gaussian) variate XNormalDistribution[μ,σ]. Instead, the term "inverse" in InverseGaussianDistribution refers to the fact that the time a Brownian motion with positive drift takes to reach a fixed positive level is distributed according to an inverse Gaussian distribution, while the Gaussian distribution describes the level of a Brownian motion at a fixed time. In addition to its role in Brownian motion, InverseGaussianDistribution is used as a tool in the study of Wiener processes, engineering, reliability theory, occupational exposure data, risk analysis, and actuarial statistics.
RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from an inverse Gaussian distribution. Distributed[x,InverseGaussianDistribution[μ,λ,θ]], written more concisely as xInverseGaussianDistribution[μ,λ,θ], can be used to assert that a random variable x is distributed according to an inverse Gaussian distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
The probability density and cumulative distribution functions for inverse Gaussian distributions may be given using PDF[InverseGaussianDistribution[μ,λ,θ],x] and CDF[InverseGaussianDistribution[μ,λ,θ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
DistributionFitTest can be used to test if a given dataset is consistent with an inverse Gaussian distribution, EstimatedDistribution to estimate an inverse Gaussian parametric distribution from given data, and FindDistributionParameters to fit data to an inverse Gaussian distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic inverse Gaussian distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic inverse Gaussian distribution.
TransformedDistribution can be used to represent a transformed inverse Gaussian distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain an inverse Gaussian distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving inverse Gaussian distributions.
InverseGaussianDistribution is closely related to a number of other distributions. For example, it is related to NormalDistribution in the sense that the CumulantGeneratingFunction for NormalDistribution is inverse to that of an unscaled InverseGaussianDistribution. InverseGaussianDistribution has GammaDistribution, InverseGammaDistribution, and HyperbolicDistribution as limiting cases. InverseGaussianDistribution is also related to WeibullDistribution, LogNormalDistribution, ChiSquareDistribution, InverseChiSquareDistribution, and FRatioDistribution.

Examples

open allclose all

Basic Examples (6)Summary of the most common use cases

Probability density function:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-js36e9

Out[3]=3

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-lagt4d

Out[2]=2

Cumulative distribution function of an inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-2h94we

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-4m5b0q

Out[2]=2

Probability density function of a generalized inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-c4waj3

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-cncdxc

Out[2]=2

Cumulative distribution function of a generalized inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-rx1jr5

Out[1]=1

Mean:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-ivzok8

Out[1]=1

Mean of a generalized inverse Gaussian distribution:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-r8b1f3

Out[2]=2

Variance:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-79g6c0

Out[1]=1

Variance of a generalized inverse Gaussian distribution:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-7o18wz

Out[2]=2

Scope (10)Survey of the scope of standard use cases

Generate a sample of random numbers from an inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-qhtk5j

Compare its histogram to the PDF:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-03mwaz

Out[3]=3

Generate a set of random numbers distributed according to a generalized inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-pcg0o

Compare its histogram to the PDF:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-qhsa5s

Out[2]=2

Distribution parameters estimation:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-45b7g2

Estimate the distribution parameters from sample data:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-epi747

Out[2]=2

Compare a density histogram of the sample with the PDF of the estimated distribution:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-c3eeq0

Out[3]=3

Skewness:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-qfmjnl

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-hg0

Out[2]=2

For generalized inverse Gaussian distribution:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-s6998m

Out[3]=3

Kurtosis:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-9bubyo

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-wtw

Out[2]=2

For generalized inverse Gaussian distribution:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-12w9wh

Out[3]=3

Different moments with closed forms as functions of parameters:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-js043h

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-rx074o

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-pknsqa

Out[3]=3

FactorialMoment:

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-zg9ct4

Out[4]=4

In[5]:=5

✖

https://wolfram.com/xid/0g34losaain2oz606-9gzmth

Out[5]=5

Closed form for symbolic order:

In[6]:=6

✖

https://wolfram.com/xid/0g34losaain2oz606-ud79bm

Out[6]=6

Moments for generalized inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-hncf9

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-lyd3v

Out[2]=2

Closed form for symbolic order:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-urp7q0

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-s0ctbf

Out[4]=4

FactorialMoment:

In[5]:=5

✖

https://wolfram.com/xid/0g34losaain2oz606-4vvw6n

Out[5]=5

In[6]:=6

✖

https://wolfram.com/xid/0g34losaain2oz606-3r0gwf

Out[6]=6

Hazard function of inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-utjc3n

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-yc11ft

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-yv7v1r

Out[3]=3

Hazard function of generalized inverse Gaussian distribution:

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-gg13vn

Out[4]=4

Quantile function of inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-02xrl7

Out[1]=1

Quantile function of generalized inverse Gaussian distribution:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-eefij3

Out[2]=2

Consistent use of Quantity in parameters yields QuantityDistribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-grnpzf

Out[1]=1

Find the spread of distances:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-8tfiv

Out[2]=2

Applications (3)Sample problems that can be solved with this function

Find the distribution of the time a Brownian motion with positive drift takes to reach a level of 2:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-e7ktmn

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-ic12j7

Remove empty lists and extract times:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-thhsej

Fit InverseGaussianDistribution to the data:

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-okm86v

Out[4]=4

Compare data histogram to the fitted PDF:

In[6]:=6

✖

https://wolfram.com/xid/0g34losaain2oz606-bxzbfs

Out[6]=6

The lifetime of a device has an inverse Gaussian distribution. Find the reliability of the device:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-4m8ue6

Out[1]=1

The failure rate for and :

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-xz8iwk

Out[2]=2

Find the maximum failure rate:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-s26gzq

Out[3]=3

The failure rate decreases to a positive value:

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-yg6f8b

Out[4]=4

Find reliability of two such devices in series:

In[5]:=5

✖

https://wolfram.com/xid/0g34losaain2oz606-yko0op

Out[5]=5

Find reliability of two such devices in parallel:

In[6]:=6

✖

https://wolfram.com/xid/0g34losaain2oz606-39ijxy

Out[6]=6

Compare reliability of both systems for and :

In[7]:=7

✖

https://wolfram.com/xid/0g34losaain2oz606-qqswjr

Out[7]=7

When a particle travels through a medium it loses energy through scattering. The energy-loss spectrum, according to an integrable model by Lindhard and Nielsen, has an InverseGaussianDistribution profile:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-fx4n16

The distribution is parametrized by its mean, which is proportional to medium thickness:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-ddwyx4

Out[2]=2

Probability density:

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-cqcd3k

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-grdjxh

Out[4]=4

Properties & Relations (6)Properties of the function, and connections to other functions

Scaling of inverse Gaussian distribution carries over the mean and the scale parameter:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-215dz0

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-e7bb40

Out[2]=2

Sum of independent identically distributed variables following InverseGaussianDistribution follows InverseGaussianDistribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-sy512r

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-x7syo6

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-u3lj04

Out[3]=3

Find the distribution of the sum using TransformedDistribution:

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-m1uw99

Out[4]=4

The mean of identical inverse Gaussian distributions has an inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-lza64k

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-9cmq03

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-q0snku

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-zgltbg

Out[4]=4

The sum of inverse Gaussian distribution variates with follows an inverse Gaussian distribution:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-l21jm9

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-emjkfk

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-d096eb

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0g34losaain2oz606-21fomm

Out[4]=4

Relationships to other distributions:

Generalized inverse Gaussian distribution simplifies to inverse Gaussian distribution for :

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-3oh749

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-rz9omu

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0g34losaain2oz606-zay6yv

Out[3]=3

Possible Issues (2)Common pitfalls and unexpected behavior

InverseGaussianDistribution is not defined when μ is not a positive real number:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-d3r

Out[1]=1

InverseGaussianDistribution is not defined when λ is not a positive real number:

In[2]:=2

✖

https://wolfram.com/xid/0g34losaain2oz606-hel

Out[2]=2

Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-t70

Out[1]=1

Neat Examples (1)Surprising or curious use cases

PDFs for different λ values with CDF contours:

In[1]:=1

✖

https://wolfram.com/xid/0g34losaain2oz606-io0104

In[5]:=5

✖

https://wolfram.com/xid/0g34losaain2oz606-ceikus

Out[5]=5

Top