WindingCount

WindingCount[contour,p]

给出闭合曲线环绕点 p 的次数.

更多信息和选项

  • WindingCount 亦称为环绕数.
  • WindingCount 通常用于根据自相交闭合曲线定义多边形.
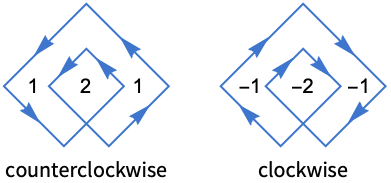
  • 逆时针方向环绕的值为 1，顺时针方向环绕的值为 -1. 对于多个环线 (contour)，环绕点 p 的次数是每个环线的环绕数的和.
  • 闭合曲线 contour 通常为一组线段 Line[{{p1,p2},…,{pn-1,pn},{pn,p1}}] 且必须位于一个平面上.
  • 对于多边形 poly，WindingCount[poly,p] 给出多边形的边界线环绕点 p 的次数.

范例

打开所有单元关闭所有单元

基本范例  (1)

计算闭合曲环绕一个点的次数：

范围  (2)

计算闭合曲环绕一个点的次数：

计算多边形边界线环绕一个点的次数：

应用  (2)

求正星形多边形的多边形密度：

根据给定环线周围的点的环绕数对点进行着色：

属性和关系  (1)

CrossingCount 是替代计数函数：

可能存在的问题  (1)

多边形边界曲线始终以逆时针方向给出，没有重叠：

环绕数：

Wolfram Research (2019)，WindingCount，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WindingCount.html.

文本

Wolfram Research (2019)，WindingCount，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WindingCount.html.

CMS

Wolfram 语言. 2019. "WindingCount." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WindingCount.html.

APA

Wolfram 语言. (2019). WindingCount. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WindingCount.html 年

BibTeX

@misc{reference.wolfram_2024_windingcount, author="Wolfram Research", title="{WindingCount}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/WindingCount.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_windingcount, organization={Wolfram Research}, title={WindingCount}, year={2019}, url={https://reference.wolfram.com/language/ref/WindingCount.html}, note=[Accessed: 22-November-2024 ]}