WindingPolygon

WindingPolygon[{p1,p2,…,pn}]

閉じた輪郭線 p1,p2,…,pn,p1が少なくとも1回その周りを回転する，すべての点を表す多角形を与える．

WindingPolygon[{{p11,p12,…},{p21,p22,…},…}]

閉じた輪郭線 p11,p12,…と p21,p22,…からの多角形を与える．

WindingPolygon[…,"wrule"]

指定された回転規則"wrule"を使って多角形を定義する．

詳細とオプション

  • WindingPolygonは回転塗潰し規則としても知られている．
  • WindingPolygonは，一般に，自己交差のある閉曲線からの多角形の定義に使われる．
  • 点 p の周り閉じた輪郭線の回転数が0ではないとき，点 p は多角形の中にある．回転数はWindingCountで与えられる．
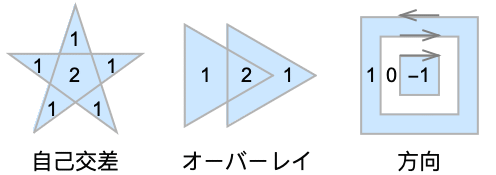
  • 以下は，各領域についての回転数である．
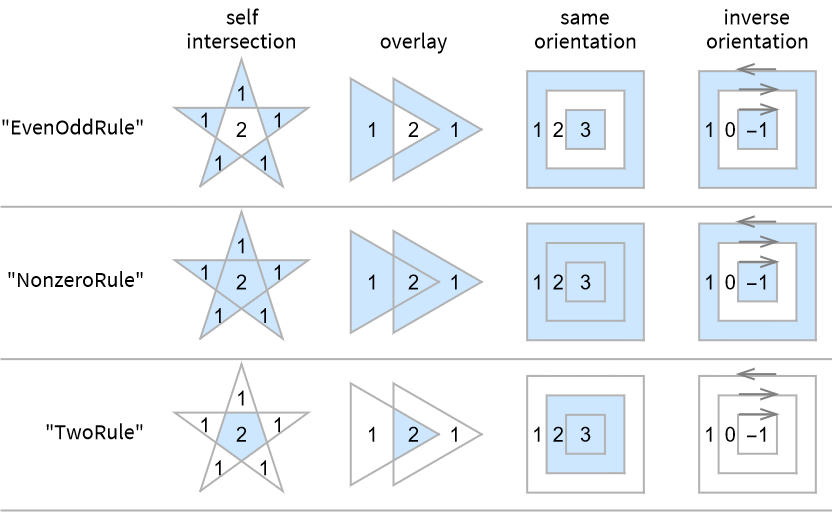
  • 回転規則"wrule"が異なると，違う多角形が与えられる．次は，可能な回転規則である．
  • WindingPolygon[{p1,p2,…}]はWindingPolygon[{p1,p2,…},"NonzeroRule"]に等しい．
  • 点 piは任意の埋込み次元を持つことができるが，すべてが1つの平面上になければならず，また，同じ埋込み次元を持たなければならない．
  • WindingPolygonにはPolygonと同じオプションが使える．

    • 全オプションのリスト

例題

すべて開くすべて閉じる

例  (2)

多角形を定義する：

自己交差する輪郭線から多角形を構築する：

その面積：

スコープ  (14)

基本的な用法  (5)

二次元の多角形を定義する：

三次元の多角形：

n 次元の多角形：

自己交差する輪郭線から多角形を構築する：

複数の輪郭線：

非零則  (3)

多角形：

三次元の多角形：

n 次元の多角形：

偶奇則  (3)

多角形：

三次元の多角形：

n 次元の多角形：

二則  (3)

多角形：

三次元の多角形：

n 次元の多角形：

オプション  (6)

VertexColors  (2)

頂点に彩色された多角形：

3D多角形の頂点の色を指定する：

VertexNormals  (1)

辺のベクトルのクロス積を使って法線ベクトルを計算する：

法線が{1,-1,1}の方向を指している三角形：

異なる法線を使うと陰影付けに影響が出る：

VertexTextureCoordinates  (3)

二次元の多角形のテクスチャマッピング：

三次元の多角形のテクスチャマッピング：

統一されていないテクスチャ座標の値を使ってテクスチャを繰り返す：

テクスチャマッピングの前にVertexColorsが来る：

アプリケーション  (3)

基本的なアプリケーション  (1)

幾何学  (1)

星形正多角形の生成：

計算幾何学  (1)

ランダムな多角形の生成：

特性と関係  (2)

WindingPolygonは，一般に，Polygonとは異なる：

CrossingPolygonは別の多角形のコンストラクタである：

考えられる問題  (2)

WindingPolygonは，常に全次元の成分を与える：

WindingPolygonの点は平面上になければならない：

Wolfram Research (2019), WindingPolygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/WindingPolygon.html.

テキスト

Wolfram Research (2019), WindingPolygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/WindingPolygon.html.

CMS

Wolfram Language. 2019. "WindingPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WindingPolygon.html.

APA

Wolfram Language. (2019). WindingPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WindingPolygon.html

BibTeX

@misc{reference.wolfram_2024_windingpolygon, author="Wolfram Research", title="{WindingPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/WindingPolygon.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_windingpolygon, organization={Wolfram Research}, title={WindingPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/WindingPolygon.html}, note=[Accessed: 22-November-2024 ]}