WindingPolygon

WindingPolygon[{p1,p2,…,pn}]

给出一个多边形，表示所有被闭合环线 p1,p2,…,pn,p1 至少环绕一次的点.

WindingPolygon[{{p11,p12,…},{p21,p22,…},…}]

根据闭合环线 p11,p12,… 和 p21,p22,… 给出一个多边形.

WindingPolygon[…,"wrule"]

用指定的环绕规则 "wrule" 定义多边形.

更多信息和选项

  • WindingPolygon 亦称为环绕填充规则(winding filling rule).
  • WindingPolygon 通常用于根据自相交闭合曲线定义多边形.
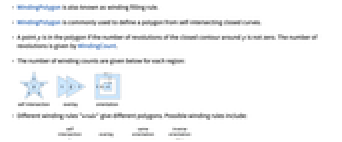
  • 如果点 p 周围的闭合环线的环绕数不为零，则点 p 属于多边形. 环绕数由 WindingCount 给出.
  • 下面给出了每个区域的环绕数：
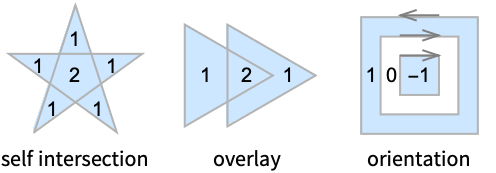
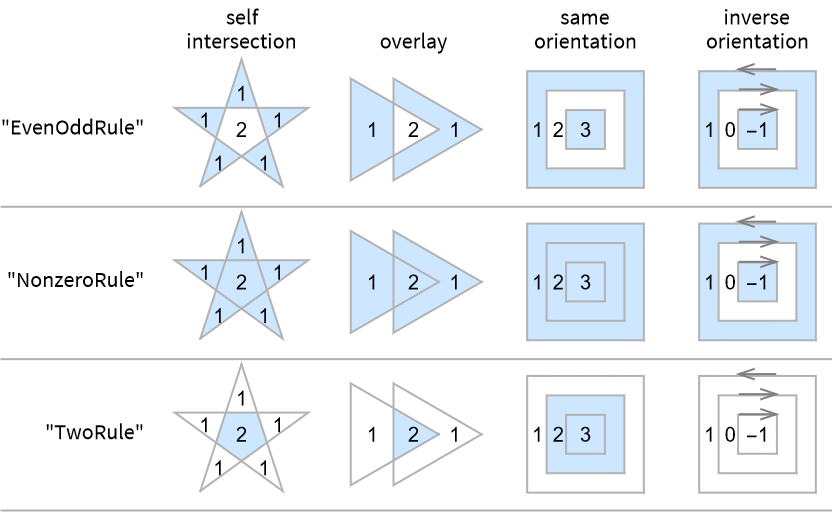
  • 不同的环绕规则 "wrule" 给出不同的多边形. 可能的环绕规则包括：
  • WindingPolygon[{p1,p2,…}] 等价于 WindingPolygon[{p1,p2,…},"NonzeroRule"].
  • 点 pi 可以有嵌入维度，但必须全部位于一个平面内并具有相同的嵌入维度.
  • WindingPolygon 和 Polygon 的选项相同.

    • 所有选项的列表

范例

打开所有单元关闭所有单元

基本范例  (2)

定义一个多边形：

根据自相交环线构建多边形：

面积：

范围  (14)

基本用法  (5)

定义一个二维多边形：

三维多边形：

n 维多边形：

根据自相交环线构建多边形：

多个环线：

Nonzero 规则  (3)

多边形：

三维多边形：

n 维多边形：

EvenOdd 规则  (3)

多边形：

三维多边形：

n 维多边形：

Two 规则  (3)

多边形：

三维多边形：

n 维多边形：

选项  (6)

VertexColors  (2)

顶点被着色的多边形：

指定三维多边形顶点的颜色：

VertexNormals  (1)

用边向量的叉积计算法向量：

法线方向为 {1,-1,1} 的三角形：

使用不同的法线将影响颜色的色度：

VertexTextureCoordinates  (3)

用二维多边形进行纹理映射：

用三维多边形进行纹理映射：

通过非统一纹理坐标值重复使用纹理：

纹理映射指令的作用出现在 VertexColors 之后：

应用  (3)

基本应用  (1)

几何  (1)

生成正星形多边形：

计算几何  (1)

生成任意多边形：

属性和关系  (2)

一般情况下，WindingPolygon 不同于 Polygon：

CrossingPolygon 是另一个多边形构造函数：

可能存在的问题  (2)

WindingPolygon 总是给出 full-dimensional 多边形：

WindingPolygon 中的点必须位于同一平面内：

Wolfram Research (2019)，WindingPolygon，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WindingPolygon.html.

文本

Wolfram Research (2019)，WindingPolygon，Wolfram 语言函数，https://reference.wolfram.com/language/ref/WindingPolygon.html.

CMS

Wolfram 语言. 2019. "WindingPolygon." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/WindingPolygon.html.

APA

Wolfram 语言. (2019). WindingPolygon. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/WindingPolygon.html 年

BibTeX

@misc{reference.wolfram_2025_windingpolygon, author="Wolfram Research", title="{WindingPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/WindingPolygon.html}", note=[Accessed: 26-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_windingpolygon, organization={Wolfram Research}, title={WindingPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/WindingPolygon.html}, note=[Accessed: 26-April-2025 ]}