WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

WinsorizedMean
✖
WinsorizedMean

Updated in 14.1

✖
WinsorizedMean[list,f]

gives the mean of the elements in list after replacing the fraction f of the smallest and largest elements by the remaining extreme values.

✖
WinsorizedMean[list,{f1,f2}]

gives the mean when the fraction f1 of the smallest elements and the fraction f2 of the largest elements are replaced by the remaining extreme values.

✖

gives the 5% winsorized mean WinsorizedMean[list,0.05].

✖
WinsorizedMean[dist,…]

gives the winsorized mean of a univariate distribution dist.

Details

  • WinsorizedMean gives a robust estimate of the mean, with more extreme values replaced by less extreme ones.
  • The winsorizing fraction is determined by the parameters f1 and f2, which indicate the fraction f1 of the smallest elements and the fraction f2 of the largest elements to be replaced by the remaining extreme values.
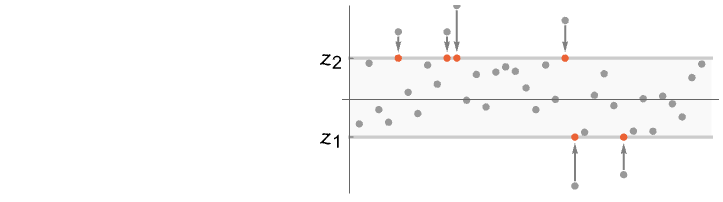
  • WinsorizedMean[list,{f1,f2}] gives the mean of Clip[list,{z1,z2}] where z1 equals RankedMin[list,1+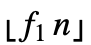], z2 equals RankedMax[list,1+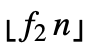], and n equals the length of list. »
  • WinsorizedMean of a univariate WeightedData data gives the weighted mean of the censored data. »
  • WinsorizedMean[{{x1,y1,…},{x2,y2,…},…},f] gives {WinsorizedMean[{x1,x2,…},f],WinsorizedMean[{y1,y2,…},f],…}. »
  • WinsorizedMean[dist,{f1,f2}] gives Mean[CensoredDistribution[Quantile[dist,{f1,1-f2}],dist]] for a univariate distribution dist. »

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Winsorized mean after removing extreme values:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-cacnen
Out[1]=1

Winsorized mean after removing the smallest extreme values:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-clbc5x
Out[1]=1

Winsorized mean of a list of dates:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-4gtmue
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ziof1v
Out[2]=2

Winsorized mean of a symbolic distribution:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-b133z2
Out[1]=1

Scope  (11)Survey of the scope of standard use cases

Data  (10)

Exact input yields exact output:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ug7y2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-bcry2t
Out[2]=2

Approximate input yields approximate output:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ksx55
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-d02ofx
Out[2]=2

Winsorized mean of a matrix gives columnwise means:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-jywoa6
Out[1]=1

Winsorized mean of a large array:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-enve04
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-if5yx4
Out[2]=2

SparseArray data can be used just like dense arrays:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-2bvdh
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-paeyu
Out[2]=2

WinsorizedMean of a univariate WeightedData:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-1jrehm
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-xm2ceq
Out[2]=2

Compare with the mean of the unweighted data:

In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-jcaudl
Out[3]=3

Winsorized mean of a TimeSeries:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-tg8p6z
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ffhpdi
Out[2]=2

The winsorized mean depends only on the values:

In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-fy9fte
Out[3]=3

Winsorized mean works with data involving quantities:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-jopin9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-e8c21s
Out[2]=2

Compute winsorized mean of dates:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-b1smxx
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-pa4nmn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-uok1il
Out[3]=3

Compute winsorized mean of times:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-et9bla
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ztsexm
Out[2]=2

List of times with different time zone specifications:

In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-mrqghz
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ow7hca
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-qyi2qe
Out[5]=5

Distributions  (1)

Winsorized mean of a univariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-rxz55
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-hbq28j
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-eiu3ke
Out[3]=3

Applications  (3)Sample problems that can be solved with this function

Obtain a robust estimate of the location when outliers are present:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-cexxtn
Out[1]=1

Extreme values have a large influence on the mean:

In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-blrzc0
Out[2]=2

Simulate a trajectory with heavy-tailed measurement noise:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-f63fz9

The underlying signal and simulated path with noise:

In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-fh1mi1
Out[2]=2

Smooth the trajectory using a moving WinsorizedMean:

In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-l6h0g9
In[4]:=4
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-brc3ht

Increasing the block size gives a smoother trajectory:

In[5]:=5
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-bb2lqb
Out[5]=5

Find a winsorized mean for the heights of children in a class:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-cevfij
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-fllmtw
Out[2]=2

The 5% winsorized mean:

In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-celepo
Out[3]=3

Compare few winsorized means:

In[4]:=4
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-q53x95
In[5]:=5
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-fgqfgk
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-cny2bx
Out[6]=6

Plot the winsorized mean as a function of the fraction parameter:

In[7]:=7
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-uog0n
In[8]:=8
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-doz2wp
Out[8]=8

Properties & Relations  (5)Properties of the function, and connections to other functions

A 0% WinsorizedMean is equivalent to Mean:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-k3hcsh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-fc96q6
Out[2]=2

WinsorizedMean approaches Median as f approaches 1/2:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-dy2d21
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-c30o90
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ed6bml
Out[3]=3

WinsorizedMean of a distribution is the mean of its CensoredDistribution:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-8ys1xn
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-gp2kyl
In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-53alj5
Out[3]=3

Mean of the CensoredDistribution with appropriate bounds:

In[4]:=4
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-nmlfvu
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-b07aaz
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-ojulil
Out[6]=6

WinsorizedMean of a sample gives an estimate of the mean of a censored distribution:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-jcz7or
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-i423fv
In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-bo98xv
Out[3]=3

Mean of the CensoredDistribution with appropriate bounds:

In[4]:=4
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-mfhhg9
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-bj114x
Out[5]=5

TrimmedMean drops the data beyond a certain quantile level, then computes the sample mean:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-cm3s6i
In[2]:=2
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-nmlm8x
In[3]:=3
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-dafzaq
Out[3]=3

WinsorizedMean clips the data beyond a certain quantile level, then computes the sample mean:

In[4]:=4
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-dsrefj
In[5]:=5
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-xbwg2
Out[5]=5

Plot the sorted data against the sample with elements removed and the clipped sample:

In[6]:=6
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-8mfiah
In[7]:=7
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-elvj1j
Out[7]=7

Possible Issues  (1)Common pitfalls and unexpected behavior

WinsorizedMean works only with numeric input:

In[1]:=1
✖
https://wolfram.com/xid/0rkva51lkq6b1p2-g88
Out[1]=1
Wolfram Research (2017), WinsorizedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/WinsorizedMean.html (updated 2024).
✖
Wolfram Research (2017), WinsorizedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/WinsorizedMean.html (updated 2024).

Text

Wolfram Research (2017), WinsorizedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/WinsorizedMean.html (updated 2024).

✖
Wolfram Research (2017), WinsorizedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/WinsorizedMean.html (updated 2024).

CMS

Wolfram Language. 2017. "WinsorizedMean." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/WinsorizedMean.html.

✖
Wolfram Language. 2017. "WinsorizedMean." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/WinsorizedMean.html.

APA

Wolfram Language. (2017). WinsorizedMean. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WinsorizedMean.html

✖
Wolfram Language. (2017). WinsorizedMean. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WinsorizedMean.html

BibTeX

@misc{reference.wolfram_2025_winsorizedmean, author="Wolfram Research", title="{WinsorizedMean}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/WinsorizedMean.html}", note=[Accessed: 22-June-2025 ]}

✖
@misc{reference.wolfram_2025_winsorizedmean, author="Wolfram Research", title="{WinsorizedMean}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/WinsorizedMean.html}", note=[Accessed: 22-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_winsorizedmean, organization={Wolfram Research}, title={WinsorizedMean}, year={2024}, url={https://reference.wolfram.com/language/ref/WinsorizedMean.html}, note=[Accessed: 22-June-2025 ]}

✖
@online{reference.wolfram_2025_winsorizedmean, organization={Wolfram Research}, title={WinsorizedMean}, year={2024}, url={https://reference.wolfram.com/language/ref/WinsorizedMean.html}, note=[Accessed: 22-June-2025 ]}