"BitVector" (Data Structure)
"BitVector"
represents a vector of Boolean values or members of a set built from an array of bits.
Details


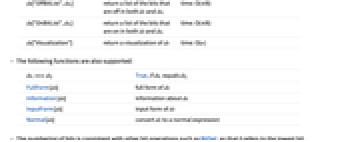
- A "BitVector" is a very compact representation of data that can only take on two values, such as Boolean data, and can also be an efficient representation of sets.
- The numbering of bits is consistent with other bit operations such as BitSet, so that 0 refers to the first bit.
-
CreateDataStructure[ "BitVector",length] create a new "BitVector" of specified length CreateDataStructure["BitVector",blist] create a new "BitVector" from a Boolean list blist with True and False elements Typed[x,"BitVector"] give x the type "BitVector" - For a data structure of type "BitVector", the following operations can be used:
-
ds["BitAnd",dsi] combine the bits in ds and dsi using bitwise And time: O(n/8) ds["BitClear",k] set the kth bit in ds to 0 time: O(1) ds["BitClearAll"] set all the bits in ds to 0 time: O(n) ds["BitCount"] return the number of bits in ds that are set to 1 time: O(n) ds["BitGet",k] get the kth bit in ds time: O(1) ds["BitInvert",k] invert the value of the kth bit of ds time: O(1) ds["BitList"] return a list of bits that are set to 1 in ds time: O(n) ds["BitNand",dsi] combine the bits in ds and dsi using bitwise Nand time: O(n/8) ds["BitNor",dsi] combine the bits in ds and dsi using bitwise Nor time: O(n/8) ds["BitNot",dsi] toggle the bits in ds time: O(n/8) ds["BitOr",dsi] combine the bits in ds and dsi using bitwise Or time: O(n/8) ds["BitSet",k] set the kth bit in ds to 1 time: O(1) ds["BitTest",k] return True if the kth bit of ds is set to 1 and False otherwise time: O(1) ds["BitXnor",dsi] combine the bits in ds and dsi using bitwise Xnor time: O(n/8) ds["BitXor",dsi] combine the bits in ds and dsi using bitwise Xor time: O(n/8) ds["Boole"] return a numeric array with ones for the set bits in ds and zeroes elsewhere. time: O(n) ds["Capacity"] return the number of bits that can be stored in ds time: O(1) ds["Copy"] return a copy of ds time: O(n) ds["Length"] return the number of bits that can be stored in ds time: O(1) ds["OffBitList"] return a list of the bits that are off in ds time: O(n/8) ds["OffBitList",dsi] return a list of the bits that are off in both ds and dsi time: O(n/8) ds["OnBitList",dsi] return a list of the bits that are on in both ds and dsi time: O(n/8) ds["Visualization"] return a visualization of ds time: O(n) - The following functions are also supported:
-
dsi===dsj True, if dsi equals dsj FullForm[ds] full form of ds Information[ds] information about ds InputForm[ds] input form of ds Normal[ds] convert ds to a normal expression
Examples
open allclose allBasic Examples (3)
A new "BitVector" can be created with CreateDataStructure:
It is possible to test if a bit is set:
Get a list of the bits that are set:
Return an expression version of ds:
The normal list can be used to create a new "BitVector" :
A visualization of the data structure can be generated:
Scope (1)
Information (1)
A new "BitVector" can be created with CreateDataStructure:
Properties & Relations (3)
The numbering for bits in a "BitVector" is consistent with Power and bit operations such as BitSet.
Both bit vectors are initialized with zeros:
Equality can be tested with SameQ:
Change one of the bit vectors by setting a bit:
The bit vectors are no longer the same:
Inequality can be tested with UnsameQ:
Get an array of zero/one values corresponding to the bits:
When the bit is set, the array value is one, otherwise zero: