"KDTree" (データ構造)

"KDTree"

実数座標集合についてのkd木の二分空間細分割を表す．

詳細

  • kd木は，次元 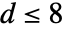での n 座標の集合を細分して，最近傍探索等の探索が素早く行えるようにするので便利である．各ノードには0と1の指標が付けられた2つのデータ要素が含まれる．データ要素は，別のkd木のノードでも，0<ik<=n である点指標のリスト {i1,i2,…}でもよい．各データ要素は固有の機械整数IDを持つ．
  • CreateDataStructure["KDTree",coordinates]すべて実数で表せる coordinates から新しい"KDTree"を作成する．
    CreateDataStructure["KDTree",coordinates, n]新しい"KDTree"を coordinates から作成し，各下位区分に最高で n 項目を含ませる．
    Typed[x,"KDTree"]x に"KDTree"型を与える．
  • "KDTree"型のデータ構造 ds には，以下の演算が使える．
  • ds["DataBounds"]座標の全体的な境界を返すtime: O(1)
    ds["DataCoordinates"]座標を返すtime: O(1)
    ds["Graphics"]2D座標について空間分割を示すtime: O(n)
    ds["ID"]ds のIDを返すtime: O(1)
    ds["ID", b]ds の b（0または1）のデータ要素についてのIDを返すtime: O(1)
    ds["Indexes",b]ds の b（0または1）の葉データ要素で表されるボックスに囲まれた座標について指標を返すtime: O(1)
    ds["LeafQ", b]ds の b（0または1）のデータ要素が葉である場合はTrueを返すtime: O(1)
    ds["Node",b]ds の b（0または1）のノードデータ要素について"KDTree"を返すtime: O(1)
    ds["SplitDimension"]ds の空間分割の次元を返すtime: O(1)
    ds["SplitPosition"]ds の空間分割の位置を返すtime: O(1)
    ds["SubtreeIndexes",sd]ds が表す部分木内の座標の指標をすべて返すtime: O(n)
    ds["SubtreeLength"]ds が表す部分木で囲まれた座標の数を求めるtime: O(n)
    ds["TreeSize"]データ要素数を返すtime: O(1)
    ds["Visualization"]ds の可視化を返すtime: O(n)

例題

すべて開くすべて閉じる

例  (1)

新しい"KDTree"オブジェクトは，CreateDataStructureを使って作成できる：

2Dデータのグラフィックスを示す：

0と1のデータ要素のいずれかが葉であるかどうかを検証する：

1データ要素の葉に含まれる点を得て，それらをグラフィックス内で赤色でハイライトする：

0データ要素で表されるkd木を得る：

このグラフィックスでは，部分木に含まれない座標部分はピンクに色付けられる：

kd木の木構造を可視化する：

kd木について分割の次元と位置を得る：

kd木の1要素データについて座標指標を得る：

座標がすべて分割次元の分割位置より上にあるかどうかを検証する：

1要素部分木のkd木について座標指標を得て，それらがすべて分割位置の下にあることを確かめる：

スコープ  (3)

情報  (1)

新しい"KDTree"は，CreateDataStructureを使って作成できる：

データ構造 ds についての情報：

葉のサイズ  (1)

CreateDataStructureの追加の引数として指定できる，最高で指定数の座標が各ボックスに含まれるまで，分割が行われる．

座標の数を最高で5までに限る：

デフォルトは，葉に対する構築および走査の費用と演算の費用との間のバランスをよくするように選ばれる：

任意精度  (1)

座標にMachinePrecisionの数値よりも高い精度の座標を与えると，適切な精度で計算が行われる：

アプリケーション  (2)

最近傍検索  (1)

"KDTree"データ構造を使うプログラムを設定して，与えられた点に最も近い座標集合内の要素を求める：

各ノードで，点がある，あるいは1つ目に最も近い辺を処理する：

葉のデータ要素についてすべての点を検証し，ノードのデータ構造について再帰的に処理する：

3つの次元で100万個の座標の集合について関数を検証する：

Nearestが返す結果を比べる：

すべての点のNormだけを計算した場合の計算時間と比べる：

kd木の構築は，単一探索より時間がかかるが，複数の探索が必要な場合には余分に時間をかける価値がある：

範囲探索  (1)

"KDTree"オブジェクトを使って，与えられた範囲内の座標の集合においてすべての要素を求めるプログラムを設定する：

各ノードにおいて，ノード分割の次元の範囲に合う各辺を処理する：

葉のデータ要素について含める点すべてを検証し，ノードのデータ要素について再帰的に処理する：

選択した特性が分かっている国すべてについてのその特性のデータ集合である：

対応する数値データを得て，それから"KDTree"データ構造を作成する：

人口が100万人未満で，国内総生産が100億ドルを超える国を求める：

人口が1000万人を超え，面積が100000km2未満の国を求める：