WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"KernelDensityEstimation" (Machine Learning Method)

  • Method for LearnDistribution.
  • Models probability density with a mixture of simple distributions.

Details & Suboptions

  • "KernelDensityEstimation" is a nonparametric method that models the probability density of a numeric space with a mixture of simple distributions (called kernels) centered around each training example, as in KernelMixtureDistribution.
  • The probability density function for a vector is given by 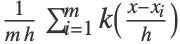for a kernel function , kernel size 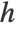and a number of training examples m.
  • The following options can be given:
  • Method "Fixed"kernel size method
    "KernelSize" Automaticsize of the kernels when Method"Fixed"
    "KernelType" "Gaussian"type of kernel used
    "NeighborsNumber" Automatickernel size expressed as a number of neighbors
  • Possible settings for "KernelType" include:
  • "Gaussian"each kernel is a Gaussian distribution
    "Ball"each kernel is a uniform distribution on a ball
  • Possible settings for Method include:
  • "Adaptive"kernel sizes can differ from each other
    "Fixed"all kernels have the same size
  • When "KernelType""Gaussian", each kernel is a spherical Gaussian (product of independent normal distributions 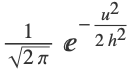), and "KernelSize" h refers to the standard deviation of the normal distribution.
  • When "KernelType""Ball", each kernel is a uniform distribution inside a sphere, and "KernelSize" refers to the radius of the sphere.
  • The value of "NeighborsNumber"k is converted into kernel size(s), so that a kernel centered around a training example typically "contains" k other training examples. If "KernelType""Ball", "contains" refers to examples that are inside the ball. If "KernelType""Gaussian", "contains" refers to examples that are inside a ball of radius h 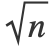where n is the dimension of the data.
  • When Method"Fixed" and "NeighborsNumber"k, a unique kernel size is found such that training examples contain on average k other examples.
  • When Method"Adaptive" and "NeighborsNumber"k, each training example adapts its kernel size such that it contains about k other examples.
  • Because of preprocessing, the "NeighborsNumber" option is typically a more convenient way to control kernel sizes than "KernelSize". When Method"Fixed", the value of "KernelSize" supersedes the value of "NeighborsNumber".
  • Information[LearnedDistribution[…],"MethodOption"] can be used to extract the values of options chosen by the automation system.
  • LearnDistribution[…,FeatureExtractor"Minimal"] can be used to remove most preprocessing and directly access the method.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Train a "KernelDensityEstimation" distribution on a numeric dataset:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-6wc05d
Out[1]=1

Look at the distribution Information:

In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-zci6sv
Out[2]=2

Obtain options information:

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-d4gaww
Out[3]=3

Obtain an option value directly:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-tm1l4s
Out[4]=4

Compute the probability density for a new example:

In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-37we6q
Out[5]=5

Plot the PDF along with the training data:

In[6]:=6
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-jfmxrj
Out[6]=6

Generate and visualize new samples:

In[7]:=7
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-trbtxb
Out[7]=7

Train a "KernelDensityEstimation" distribution on a two-dimensional dataset:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-g4novm
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-4ewt2p
Out[2]=2

Plot the PDF along with the training data:

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-i4ttni
Out[3]=3

Use SynthesizeMissingValues to impute missing values using the learned distribution:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-og5slp
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-feqqk1
Out[5]=5

Train a "KernelDensityEstimation" distribution on a nominal dataset:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-36gxxt
Out[1]=1

Because of the necessary preprocessing, the PDF computation is not exact:

In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-wbm3in
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-jokluj
Out[3]=3

Use ComputeUncertainty to obtain the uncertainty on the result:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-29ml4l
Out[4]=4

Increase MaxIterations to improve the estimation precision:

In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-5lufi6
Out[5]=5

Options  (4)Common values & functionality for each option

"KernelSize"  (1)

Train a kernel mixture distribution with a kernel size of 0.2:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-vthdnl
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-g542sp
Out[2]=2

Evaluate the PDF of the distribution at a specific point:

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-89877v
Out[3]=3

Visualize the PDF obtained after training a kernel mixture distribution with various kernel sizes:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-5bujoz
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-yv7v8r
Out[5]=5

"KernelType"  (1)

Train a "KernelDensityEstimation" distribution with a "Ball" kernel:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-iu3rlx
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-sltk9u
Out[2]=2

Evaluate the PDF of the distribution at a specific point:

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-v8vvn8
Out[3]=3

Visualize the PDF obtained after training a kernel mixture distribution with a "Ball" and a "Gaussian" kernel:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-hbjlx6
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-u1a9s8
Out[5]=5

Method  (1)

Train a "KernelDensityEstimation" distribution with the "Adaptive" method:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-8n9io9
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-vfl8ow
Out[2]=2

Evaluate the PDF of the distribution at a specific point:

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-di1qkj
Out[3]=3

Visualize the PDF obtained after training a kernel mixture distribution with a "Ball" and a "Gaussian" kernel:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-xakq2r
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-3grodf
Out[5]=5

"NeighborsNumber"  (1)

Train a kernel mixture distribution with a kernel size of about 10 neighbors:

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-eon6sf
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-bgqzxr
Out[2]=2

Evaluate the PDF of the distribution at a specific point:

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-rhff7t
Out[3]=3

Visualize the PDF obtained after training a kernel mixture distribution with various kernel sizes expressed as neighbors numbers:

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-9hnbl1
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-4fzufa
Out[5]=5