WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

"KernelDensityEstimation" (機械学習メソッド)

  • LearnDistributionのメソッド
  • 確率密度を単純分布の混合でモデル化する．

詳細とサブオプション

  • "KernelDensityEstimation"は，KernelMixtureDistributionにおけるように，数値空間の確率密度を各訓練例周辺を中心とした（カーネルと呼ばれる）単純分布でモデル化するノンパラメトリックメソッドである．
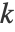  • ベクトル の確率密度関数は，カーネル関数 ，カーネルサイズ 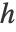，訓練例の数 m について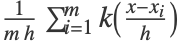，で与えられる．
  • 次は，使用可能なオプションである．
  • Method "Fixed"カーネルサイズメソッド
    "KernelSize" AutomaticMethod"Fixed"のときのカーネルサイズ
    "KernelType" "Gaussian"使用されているカーネルタイプ
    "NeighborsNumber" Automatic近傍数として表されたカーネルサイズ
  • 次は，"KernelType"の可能な設定である．
  • "Gaussian"各カーネルはガウス分布である
    "Ball"各カーネルは球面上の一様分布である
  • 次は，Methodの可能な設定である．
  • "Adaptive"個々のカーネルサイズは違ってよい
    "Fixed"全てのカーネルが同じサイズである
  • "KernelType""Gaussian"のとき，各カーネルは球面ガウス分布（独立正規分布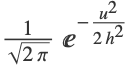の積）で，"KernelSize" h は正規分布の標準偏差を指す．
  • "KernelType""Ball"のとき，各カーネルは球内の一様分布で，"KernelSize"は球の半径を指す．
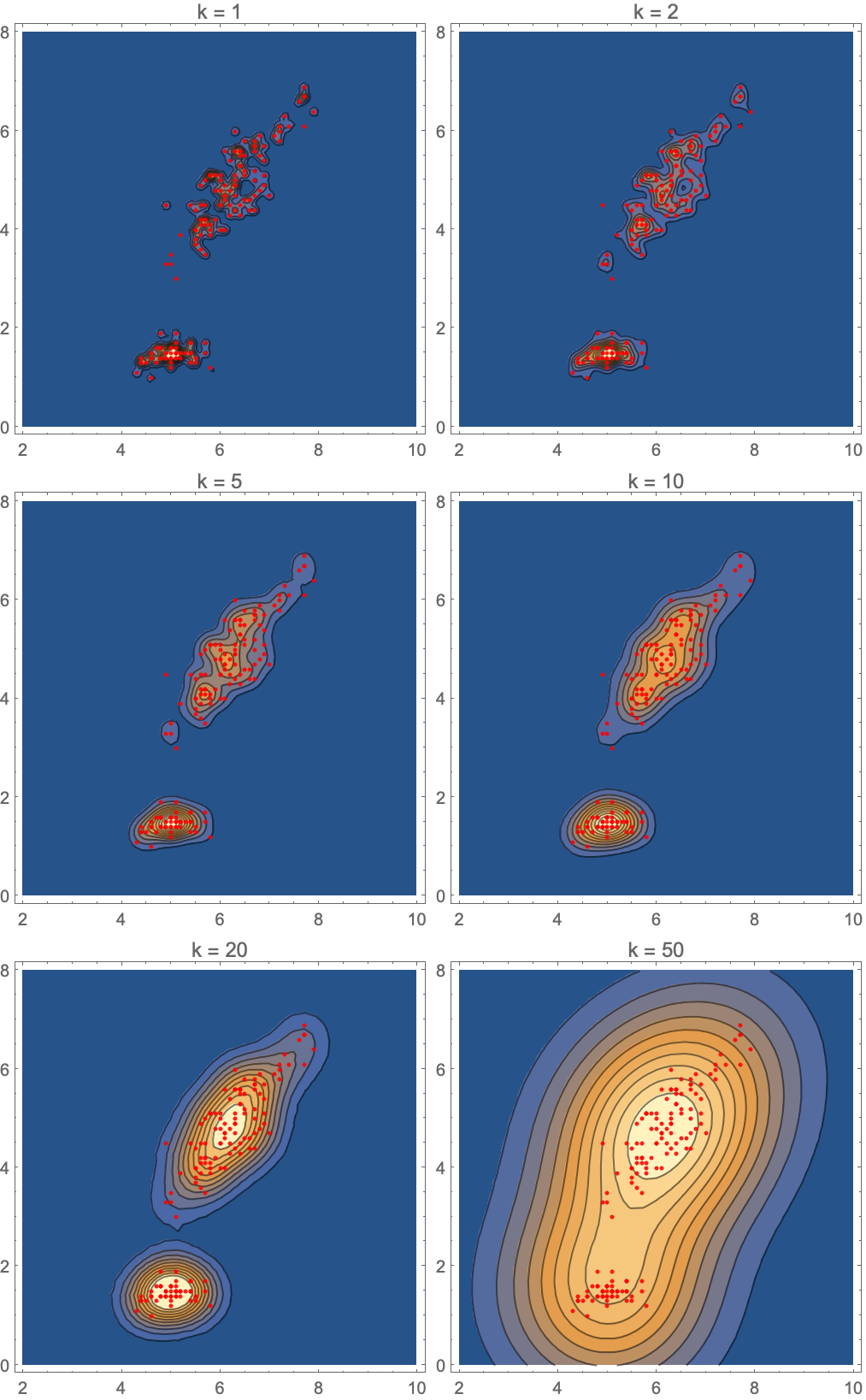
  • "NeighborsNumber"k の値は，訓練例の周りを中心とするカーネルが k 個の他の訓練例を含むように，カーネルサイズに変換される．"KernelType""Ball"のとき，"contains"は球内の例を指す． "KernelType""Gaussian"であれば，"contains"は半径 h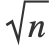の球内の例を指す．ただし，n はデータの次元である．
  • Method"Fixed"で"NeighborsNumber"k のときは，訓練例が平均 k 個の他の例を含むように一意的なカーネルサイズが求められる．
  • Method"Adaptive"で"NeighborsNumber"k のときは，各訓練例が，カーネルに k 個の他の例が含まれるように，カーネルサイズを適応させる．
  • 前処理のために，"NeighborsNumber"オプションは，通常，カーネルサイズを制御する上で"KernelSize"より便利な方法である．Method"Fixed"のときは，"KernelSize"の値が"NeighborsNumber"の値を上書きする．
  • Information[LearnedDistribution[…],"MethodOption"]を使って自動システムによって選択されたオプションの値を抽出することができる．
  • LearnDistribution[…,FeatureExtractor"Minimal"]を使ってほとんどの前処理を削除してメソッドに直接アクセスすることができる．

例題

すべて開くすべて閉じる

例  (3)基本的な使用例

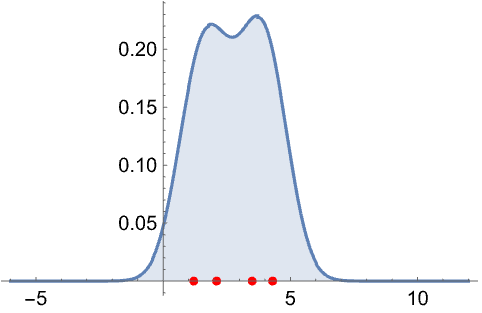
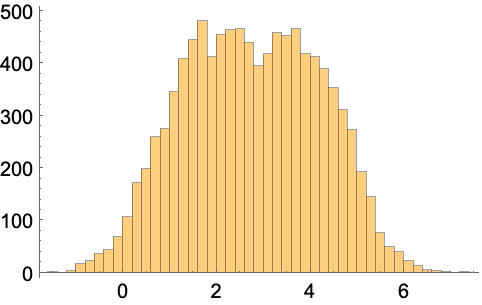
"KernelDensityEstimation"分布を数値データ集合で訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-6wc05d
Out[1]=1

分布の情報(Information)を見る：

In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-zci6sv
Out[2]=2

オプション情報を入手する：

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-d4gaww
Out[3]=3

オプションの値を直接得る：

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-tm1l4s
Out[4]=4

新たな例の確率密度を計算する：

In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-37we6q
Out[5]=5

確率密度関数(PDF)を訓練データと一緒にプロットする：

In[6]:=6
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-jfmxrj
Out[6]=6

新たなサンプルを生成し，可視化する：

In[7]:=7
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-trbtxb
Out[7]=7

"KernelDensityEstimation"分布を二次元データ集合で訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-g4novm
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-4ewt2p
Out[2]=2

PDFを訓練データと一緒にプロットする：

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-i4ttni
Out[3]=3

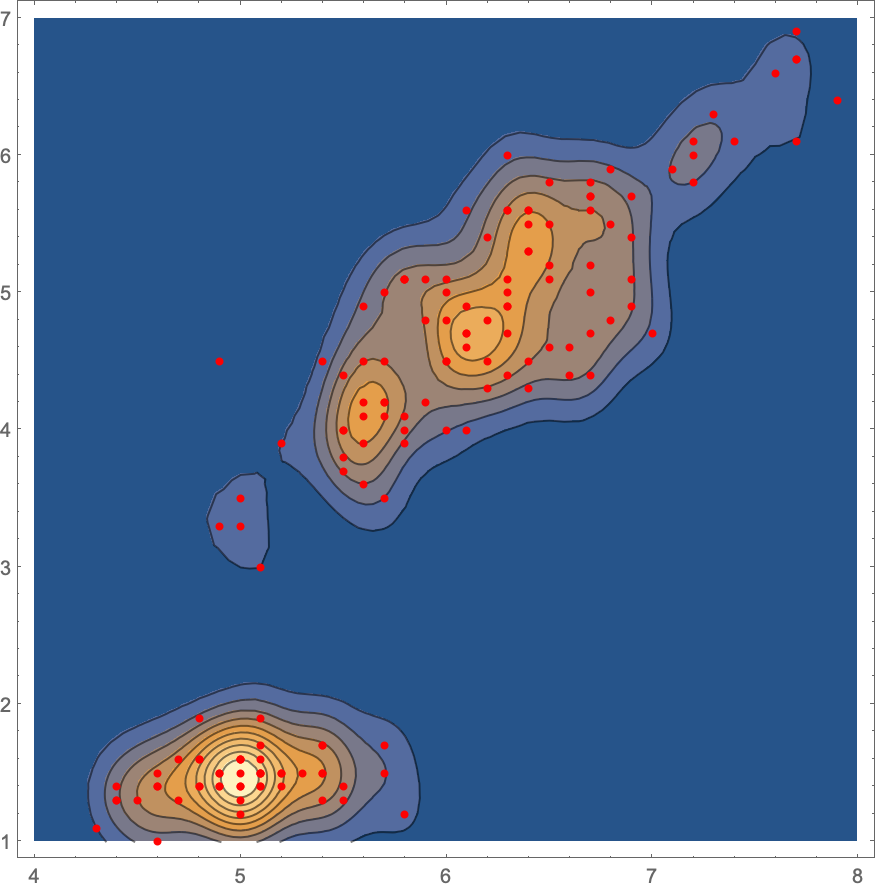
SynthesizeMissingValuesを使い，学習済みの分布を使って欠落値を転嫁する：

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-og5slp
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-feqqk1
Out[5]=5

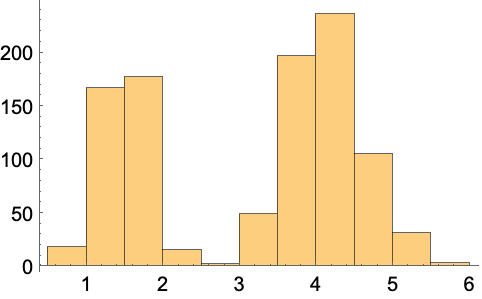
"KernelDensityEstimation"分布を名義的データ集合で訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-36gxxt
Out[1]=1

前処理が必要なので，PDFの計算は厳密ではない：

In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-wbm3in
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-jokluj
Out[3]=3

ComputeUncertaintyを使って結果の不確かさを得る：

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-29ml4l
Out[4]=4

MaxIterationsを大きくすると推定精度が上がる：

In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-5lufi6
Out[5]=5

オプション  (4)各オプションの一般的な値と機能

"KernelSize"  (1)

カーネル混合分布を0.2のカーネルサイズで訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-vthdnl
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-g542sp
Out[2]=2

分布のPDFを特定の点で評価する：

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-89877v
Out[3]=3

カーネル混合分布をさまざまなカーネルサイズで訓練した後で得られたPDFを可視化する：

In[4]:=4
✖
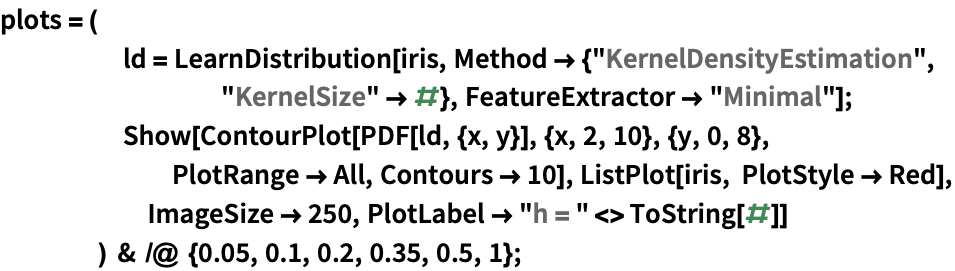
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-5bujoz
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-yv7v8r
Out[5]=5

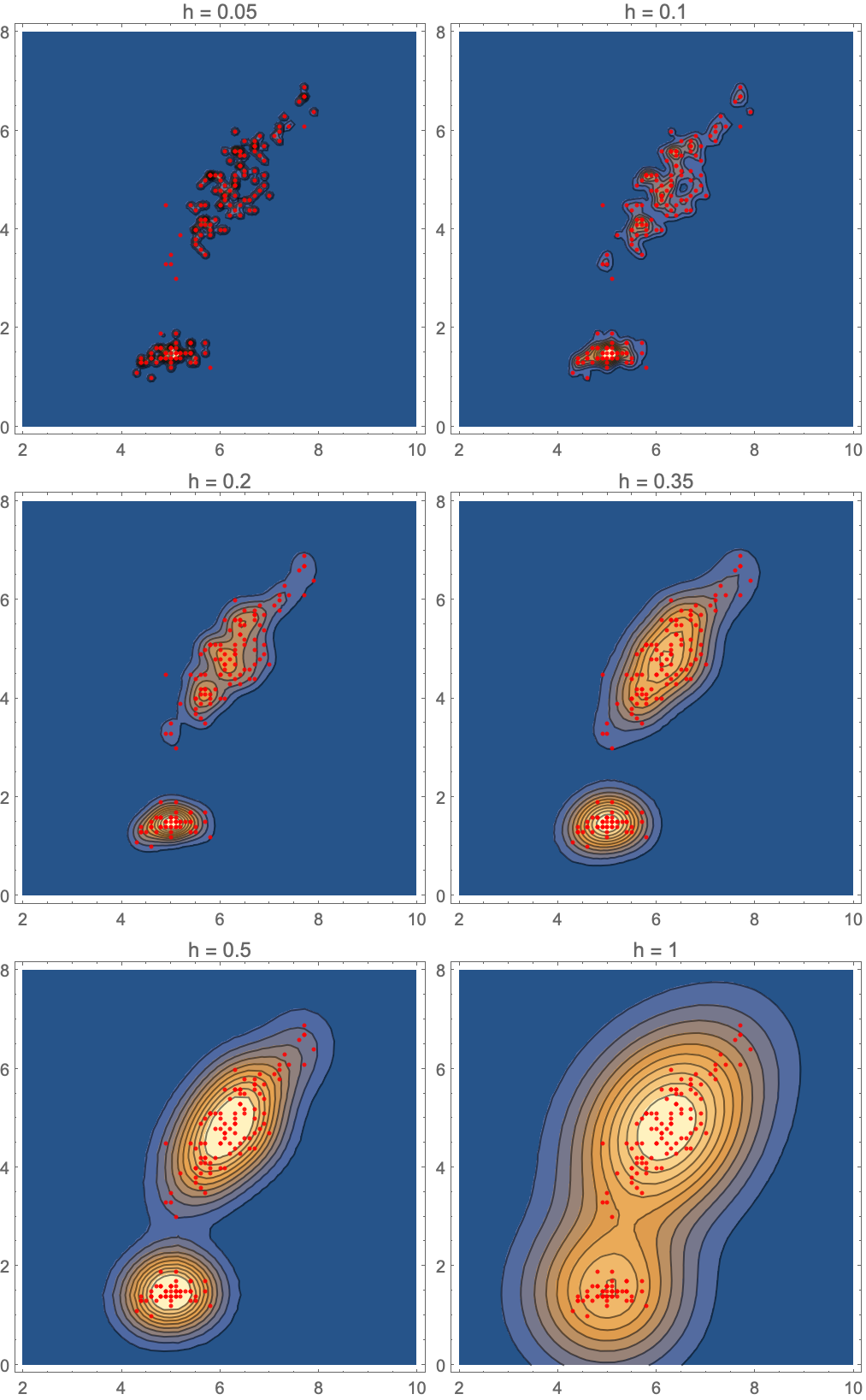
"KernelType"  (1)

"KernelDensityEstimation"分布を"Ball"カーネルで訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-iu3rlx
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-sltk9u
Out[2]=2

分布のPDFを特定の点で評価する：

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-v8vvn8
Out[3]=3

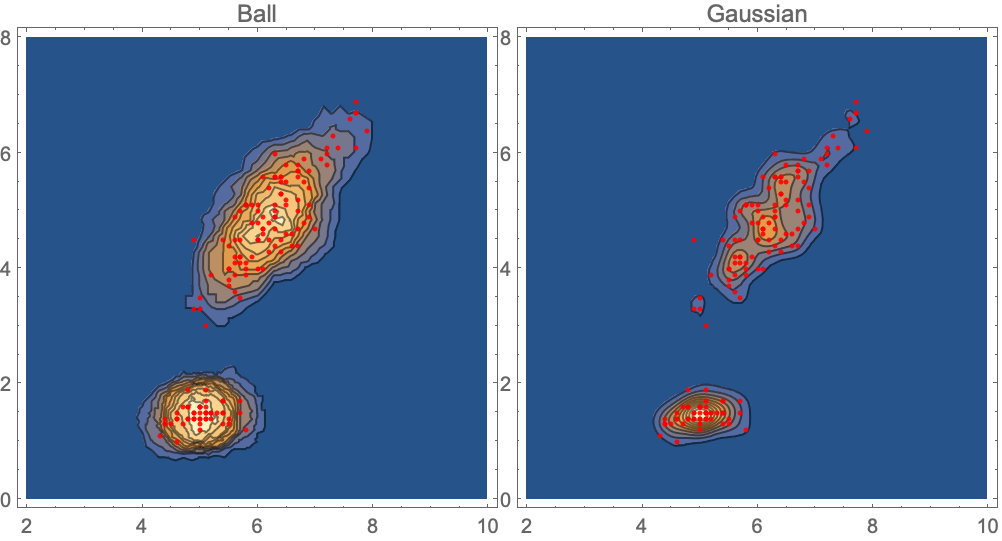
カーネル混合分布を"Ball"カーネルおよび"Gaussian"カーネルで訓練した後で得られたPDFを可視化する：

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-hbjlx6
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-u1a9s8
Out[5]=5

Method  (1)

"KernelDensityEstimation"分布を"Adaptive"メソッドで訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-8n9io9
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-vfl8ow
Out[2]=2

分布のPDFを特定の点で評価する：

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-di1qkj
Out[3]=3

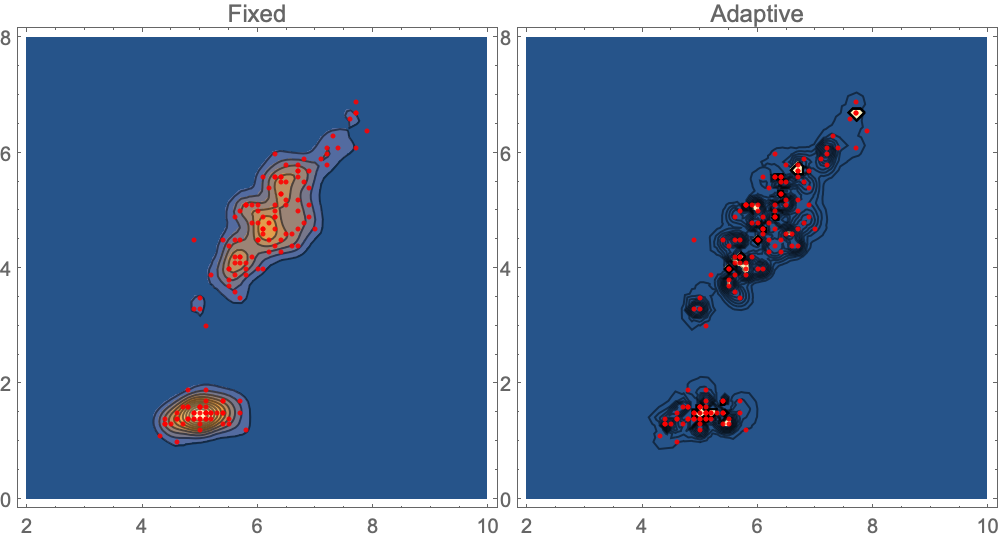
カーネル混合分布を"Ball"カーネルと"Gaussian"カーネルで訓練した後で得られたPDFを可視化する：

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-xakq2r
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-3grodf
Out[5]=5

"NeighborsNumber"  (1)

約10の近傍のカーネルサイズでカーネル混合分布を訓練する：

In[1]:=1
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-eon6sf
In[2]:=2
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-bgqzxr
Out[2]=2

分布のPDFを特定の点で評価する：

In[3]:=3
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-rhff7t
Out[3]=3

カーネル混合分布を近傍数で表されたさまざまなカーネルサイズで訓練した後で得られたPDFを可視化する：

In[4]:=4
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-9hnbl1
In[5]:=5
✖
https://wolfram.com/xid/0zyl7urlsg0ch3qjq-4fzufa
Out[5]=5