WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"LinearRegression" (Machine Learning Method)

  • Method for Predict.
  • Predict values using a linear combination of features.

Details & Suboptions

  • The linear regression predicts the numerical output y using a linear combination of numerical features 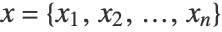. The conditional probability 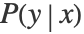is modeled according to 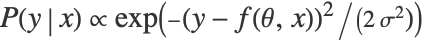, with .
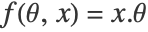  • The estimation of the parameter vector θ is done by minimizing the loss function 1/2sum_(i=1)^m(y_i-f(theta,x_i))^2+lambda_1sum_(i=1)^nTemplateBox[{{theta, _, i}}, Abs]+(lambda_2)/2 sum_(i=1)^ntheta_i^2, where m is the number of examples and n is the number of numerical features.
  • The following suboptions can be given:
  • "L1Regularization" 0value of 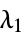in the loss function
    "L2Regularization" Automaticvalue of 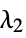iin the loss function
    "OptimizationMethod" Automaticwhat optimization method to use
  • Possible settings for the "OptimizationMethod" option include:
  • "NormalEquation"linear algebra method
    "StochasticGradientDescent"stochastic gradient method
    "OrthantWiseQuasiNewton"orthant-wise quasi-Newton method
  • For this method, Information[PredictorFunction[…],"Function"] gives a simple expression to compute the predicted value from the features.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Train a predictor on labeled examples:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-wxc5bs
Out[1]=1

Look at the Information:

In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-3656v8
Out[2]=2

Predict a new example:

In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-tgze8s
Out[3]=3

Generate two-dimensional data:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-ef76x2
Out[1]=1

Train a predictor function on it:

In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-fj7crm
Out[2]=2

Compare the data with the predicted values and look at the standard deviation:

In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-bcq515
Out[3]=3

Options  (5)Common values & functionality for each option

"L1Regularization"  (2)

Use the "L1Regularization" option to train a predictor:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-8d3hj3
Out[1]=1

Generate a training set and visualize it:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-z6fnrr
Out[1]=1

Train two predictors by using different values of the "L1Regularization" option:

In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-qm6f1x
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-718tom
Out[3]=3

Look at the predictor function to see how the larger L1 regularization has forced one parameter to be zero:

In[4]:=4
✖
https://wolfram.com/xid/0bqb5x3dcmnm-hs69mo
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bqb5x3dcmnm-psj2uv
Out[5]=5

"L2Regularization"  (2)

Use the "L2Regularization" option to train a predictor:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-zbcx6b
Out[1]=1

Generate a training set and visualize it:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-zfni0z
Out[1]=1

Train two predictors by using different values of the "L2Regularization" option:

In[2]:=2
✖
https://wolfram.com/xid/0bqb5x3dcmnm-6md8tb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bqb5x3dcmnm-z9k0eu
Out[3]=3

Look at the predictor functions to see how the L2 regularization has reduced the norm of the parameter vector:

In[4]:=4
✖
https://wolfram.com/xid/0bqb5x3dcmnm-8l4sma
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bqb5x3dcmnm-chnthl
Out[5]=5

"OptimizationMethod"  (1)

Generate a large training set:

In[1]:=1
✖
https://wolfram.com/xid/0bqb5x3dcmnm-9l9jxc

Train predictors with different optimization methods and compare their training times:

In[4]:=4
✖
https://wolfram.com/xid/0bqb5x3dcmnm-wvgecx
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bqb5x3dcmnm-ch9ek5
Out[5]=5