WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"MeanShift" (Machine Learning Method)

Details & Suboptions

  • "MeanShift" is a density-based clustering method where the density is estimated using a neighbor-based approach. "MeanShift" works for arbitrary cluster shapes and sizes; however, it can fail when clusters have different densities or are intertwined.
  • The following plots show the results of the "MeanShift" method applied to toy datasets:
  • The "MeanShift" method iteratively shifts data points toward higher-density regions. During this procedure, data points tend to collapse to different fixed points, each of them representing a cluster.
  • Formally, at each step, each data point is set to 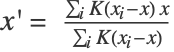with , 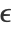defining an effective neighborhood radius. The difference is called mean shift. The algorithm repeats the mean-shift updates until points stop moving; all points belonging to a cluster are then collapsed (up to a tolerance). This algorithm is equivalent to the "NeighborhoodContraction" method but with a different neighborhood definition.
  • The option DistanceFunction can be used to define which distance to use.
  • The following suboption can be given:
  • "NeighborhoodRadius" Automaticradius ϵ

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Find clusters of nearby values using the "MeanShift" clustering method:

In[1]:=1
✖
https://wolfram.com/xid/0hlsq25mei-wxc5bs
Out[1]=1

Train the ClassifierFunction on a list of colors using the "MeanShift" method:

In[1]:=1
✖
https://wolfram.com/xid/0hlsq25mei-509fvf
Out[1]=1

Gather the elements by their class number:

In[2]:=2
✖
https://wolfram.com/xid/0hlsq25mei-izazxv
Out[2]=2

Train a ClassifierFunction on a list of strings:

In[1]:=1
✖
https://wolfram.com/xid/0hlsq25mei-nog76a
Out[1]=1

Find the cluster assignments and gather the elements by their cluster:

In[2]:=2
✖
https://wolfram.com/xid/0hlsq25mei-lkm67v
Out[2]=2
Out[2]=2

Options  (3)Common values & functionality for each option

DistanceFunction  (1)

Cluster data using Manhattan distance:

In[1]:=1
✖
https://wolfram.com/xid/0hlsq25mei-xbfrhk
Out[1]=1

"NeighborhoodRadius"  (2)

Find clusters by specifying the "NeighborhoodRadius" suboption:

✖
https://wolfram.com/xid/0hlsq25mei-pibiva

Generate a list of 100 random colors:

In[1]:=1
✖
https://wolfram.com/xid/0hlsq25mei-p4t1fk
Out[1]=1

Cluster the colors using the "MeanShift" method:

In[2]:=2
✖
https://wolfram.com/xid/0hlsq25mei-f56t7r
Out[2]=2

Try different "NeighborhoodRadius" suboptions for clustering the colors:

In[3]:=3
✖
https://wolfram.com/xid/0hlsq25mei-72cbi2
Out[3]=3