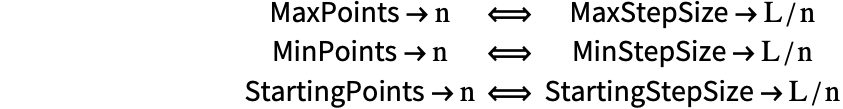はじめに

線の方法による数値解法とは，偏微分方程式を解くための方法である．まず，1つの次元以外のすべての次元で離散化し，その準離散的な問題を常微分方程式(ODE)あるいは微分代数方程式(DAE)系として積分するものである．このメソッドの大きな利点は，ODEとDAEを数値的に積分するために開発された高度な汎用メソッドとソフトウェアが利用できる点である．線の方法が適用できるPDEでは，このメソッドが非常に有効であることが多い．

ODEとDAEの積分法には，初期値（コーシー(Cauchy)）問題のソルバが使われるので，PDEの問題は少なくとも一次元の初期値問題として整っているものでなければならない．このため，ラプラス(Laplace)方程式のような純粋な楕円方程式は除外されるが，効率的に解くことのできる大部分の発展方程式は残される．

このメソッドの基本的な考えは，言葉だけで説明するよりも簡単な例題を見てた方が分かりやすいだろう．次の問題（地中熱の季節による変化を表す簡単なモデル）を考えてみよう．

この問題には初期値 があるので，線の方法が適用できる可能性がある．

問題(1)は変数 について，二次有限差分（その中でも次の近似）を用いて離散化される．

有限差分法による離散化は最も一般的なものではあるが，線の方法における離散化は有限差分法を用いて行われなければならない訳ではない．有限体積法や有限要素法による離散化を使ってもよい．

上記の有限差分法による離散化を使う場合は，一様格子 を選ぶ．ここで， であり， になるような間隔 が取ってある．を の値としよう．問題の設定を例示するために， の特定の値を選ぶ．

以下は の特定の値と，後続のコマンドで使われる の対応する値を定義する．この定義を変更することで，より密な，あるいは粗な空間近似にすることができる：

のベクトルを定義する：

では，ODE系を求めるために中心差分公式(2)を使うことができる．しかし，その前に，境界条件を組み込むと便利である．

におけるディレクレ(Dirichlet)境界条件は，を の関数として定義するだけで簡単に扱うことができる．あるいは，境界条件を時間について微分して，その微分を境界条件に加えるという方法もある．この例では後者を使う．

におけるノイマン(Neumann)境界条件は上記よりも少々難しい．二階差分でこれを処理する方法のひとつに，反射を使ったものがある．区間がで と で同じ境界条件を持つ問題を解いていると想定しよう．初期条件と境界条件は について対称なので，解は について常に対称でなければならない．このため対称性は におけるノイマン境界条件と等しくなる．従って が成り立ち，となる．

これで，この変微分方程式はNDSolveにおける常微分方程式の積分演算子によって解くことができる常微分方程式の初期値問題に部分的に離散化された．

次は解 を と の関数としてプロットしたものである：

上記のプロットはなぜこの方法が「線の方法」による数値解法と呼ばれるのかを示している．

線と線の間の解は補間で求めることができる．NDSolveがPDEについて解を計算すると，結果は二次元のInterpolatingFunctionになる．

上記で使用した という設定はあまり正確な解を与えなかった．NDSolveで解を計算するとき，格子間隔を決定するのに，初期条件に対して空間誤差の推定値が使われる．時間的（あるいは少なくても時間的だと思われる）変数の誤差は，適応型のODE積分法で処理される．

例題(1)では，問題の内容から時間と空間の区別は極めて明確であった．区別が明示的ではないときでも，このチュートリアルでは「空間」および「時間」変数と呼ぶ．「空間」変数とは，離散化の対象となる変数のことである． 「時間」変数とは積分されるODE系に残される変数のことである．

Options for NDSolve`MethodOfLines.

これらのオプションを使用する際には，線の方法の働きをよく知っていなければならない場合もある．使用法については，次のセクションで詳述する．

空間離散化のために現在実装されているメソッドは"TensorProductGrid"と"FiniteElement"である．どちらのメソッドも，離散化過程の詳細を制御するために使うことのできる独自のオプション群を持つ．"FiniteElement"メソッドは非常に汎用であり，任意に形成された領域で使える．このメソッドについてはチュートリアルをご覧いただきたい．このチュートリアルでは"TensorProductGrid"を使った離散化に焦点を当てる．

空間微分の近似

有限差分法

有限差分法の考え方の本質は，以下のような標準的な微分に具現されている．

ここでは がゼロに近付くにつれて限界を通過するのではなく，次の隣接点 までの有限空間を使って近似を得る．

テイラー(Taylor)の公式からも差分公式を導くことができる．

この公式は以下のような誤差推定（十分な滑らかさを仮定している）を与えるので，より便利である．

この公式の重要な点は，サンプル点を囲む区間に対して誤差が局所的になるために， が と の間になければならないということである．有限差分公式では誤差がステンシル，つまりサンプル点の集合に対して局所的であるのが一般的である．通常，収束等の解析では，誤差は以下のように漸近誤差で表される．

この公式は一般的に一階前進差分と呼ばれる．後退差分には が用いられる．

テイラーの公式を用いると簡単に高階近似を導くことができる．例えば，次の式

を以下の式

から減算して について解くと，以下のような一次導関数の二階中心差分公式が得られる．

上述のテイラーの公式をもう一階展開して加算し，上記の公式と合わせると，二次導関数の中心差分を得るのも困難ではない．

点と点の間が均一の刻み幅 になっているために公式を導出するのが簡単になっているが，これは必ずしも必要なことではない．例えば，二次導関数の近似は一般に以下のようになる．

ここで は局所的な格子間隔の最大値に相当する．3点近似公式の漸近誤差の次数が一次に減らされている点に注意のこと．一様格子で二次になっていたのは，偶然の約分のためである．

一般に，選択した次数の漸近誤差を持つ微分公式は，十分な数のサンプル点が使われている限りテイラーの公式から導くことができる．しかし上記のように簡単な例以外では，このメソッドは扱いにくく非効率的である．これに代る方法として多項式補間に基づいた公式化がある．テイラーの公式は十分に低次の多項式については厳密（誤差項がない）なので，有限差分式も厳密である．有限差分式が補間する多項式の微分に等しいことを示すのは困難なことではない．例えば，二次導関数についての上記の式を導く最も簡単な方法は，二次方程式を補間してその二次導関数（これは基本的に主係数である）を求めることである．

3つの点，，を補間する多項式を微分することにより，二次導関数の3点有限差分式を求める：

この形式の式では，これが事実上前進一次導関数近似と後退一次導関数近似との差分であることが簡単に分かる．偏微分方程式でよく見られる のような，微分内部に係数を含む項の場合は，このように有限差分を用いることが有益なことがある．

補間式を検討すると，微分近似を得る点は格子上にある必要はないという特性も明らかになる．微分が格子点の中間点で求めることができるスタッガード格子(staggered grid)では，一般にこの特性が使われる．

次は一様なスタッガード格子 上の二次導関数の四次近似を生成する．ここで主格子点 は 上にあり， は余りである

この式の四次誤差係数はであり，これに対して以下で導かれている標準の四次近似はである．誤差が小さくなった理由の大半はステンシルの大きさが小さくなったことに帰すことができる．

一般的に， 個の点を用いる有限差分式は，次数 の多項式で少なくとも位数 の漸近式を持つ関数について厳密である．一様格子上では，特に中心差分については，より高次の漸近的な位数を期待することができる．

有効な多項式補間の技術を用いることは係数生成の合理的な方法である．しかし，B. Fornbergが開発した有限差分の重みを生成する高速のアルゴリズム[F92], [F98]の方がより高速である．

[F98]で，Fornbergは明示的な有限差分のための1行のWolfram言語式を紹介している．

ここで は微分の階数， はステンシルに含まれる格子区間の数， は微分が近似される点とステンシルの左端との間の格子区間の数である． は整数である必要はない．非整数の値の場合は，単にスタッガード格子の近似になる． を とすると，常に中心公式が生成される．

以下は一般的に使われている有限差分式の表である．

式	誤差項

一様格子上の一次導関数の有限差分式

式	誤差項

一様格子上の二次導関数の有限差分式

この表から，式が中心から遠ざかるほど，誤差項の係数が大きく，時には何百倍にもなっていることが分かる．このため，片側微分式（境界線上等で）が必要なところでは，余分な誤差を相殺するためにより高階の式が使われることがある．

NDSolve`FiniteDifferenceDerivative

Fornberg [F92]，[F98]はまた，さほど簡潔でも簡単でもないが，より一般的で，特に非一様格子に適用可能なアルゴリズムも与えている．Wolfram言語でプログラムするのも困難ではないが，可能な限り効率的にするために，新たなカーネル関数が単純なインターフェースとして（他の追加的な機能とともに）提供されている．

微分の有限差分近似を求める

終端点における微分は片側公式を用いて計算される．上記の例題で示された式は四次精度であり，これがデフォルトである．一般に，記号的な格子および／またはデータを使った場合は記号的な式が返される．これはメソッドの分析のためには便利なことが多い．しかし，実際の数値格子に関しては，NDSolve`FiniteDifferenceDerivativeに数値格子を与えた方が，記号式を使うよりもより高速でより正確になる．

以下でから までのランダムな間隔の格子を定義する：

多次元ではNDSolve`FiniteDifferenceDerivativeはテンソル積格子上で作用するので，各次元における格子点を指定するだけでよい．

次は 方向と 方向について，格子xgridとygridを定義し，xgridとygridのテンソル積上でガウスの混合 偏微分の近似を与え，誤差の平面プロットを作成する：

値が格子座標の外積に対応する行列で与えられなければならない点に注意のこと．

NDSolve`FiniteDifferenceDerivativeは微分の和の重みは計算しない．つまり，ラプラスのような一般的な演算子を使うときは，2つの近似を合わせなければならないということである．

NDSolve`FiniteDifferenceDerivativeのオプション

PeriodicInterpolation->Trueを使うと，値の最後の点は常に最初の点に等しいので，これを省略することができる．この機能は周期境界条件を持つ偏微分方程式を解く際に便利である．

通常四階差分は，機械精度における打切り（近似）誤差と丸め誤差のバランスを程よく取る．しかし，アプリケーションによっては四階差分が過度の振動（Gibbの現象）を引き起すこともあるので，二階差分の方がよい．また，より高精度のためにはより高階の差分がよいだろう．"DifferenceOrder"の偶数値では中心式を使っている．これは一般に非中心式よりも誤差係数が小さくなる．このため，適切な場合には偶数値を勧める．

NDSolve`FiniteDifferenceDerivativeFunction

偏微分方程式の解を計算する際には，通常同じ格子上で同一の有限差分近似を異なる値に繰り返し適用する．必要な重みの計算を保存して，これを変化するデータに適用すると非常に節約できる．NDSolve`FiniteDifferenceDerivativeで関数の値を持つ（第3）引数を省略すると，結果はNDSolve`FiniteDifferenceDerivativeFunctionになる．これは反復使用のために有効な形で重み計算を保存するデータオブジェクトである．

反復使用のために有限差分の重みを計算する

標準的な出力形式は短縮されており，近似された微分演算子のみが表示される点に注意のこと．

この関数はこれを構築するために使われた特定の格子上で定義された値にしか適用できない．格子を変更する必要がある場合はNDSolve`FiniteDifferenceDerivativeを使って，格子を変更するたびに重みを生成する必要がある．しかし，NDSolve`FiniteDifferenceDerivativeFunctionオブジェクトが使える場合は評価が著しく速くなる．

NDSolve`FiniteDifferenceDerivativeFunctionは多くの場合に反復的に使うことができる．簡単な例として，境界値問題を解くための単位間隔上の選点法を考えてみる．

この単純な方法は必ずしもこの問題を解くための最良の方法とは言えない．しかし，例題としては有効である．

これは境界値問題の近似解ですべての要素が零の関数を定義する．中間ベクトルの を使い，その終点(parts{1,-1})をゼロにするのが素早く簡単に境界条件を実施する方法である． 以外の数値については評価はできない．また，TimesはListableなので，Sin[2 Pi grid] u は要素幅で縫い込まれる：

この問題の設定は非常に単純なので，さまざまな選択肢を比較してみることができる．例えば，デフォルトの四階差分を使った上記の解と二階差分を使った一般的な解とを比べてみるとする．この場合"DifferenceOrder"を変化させるだけでよい．

どちらの解の方がよいかを判断する方法のひとつに，格子を細かくしたときの収束を見るものがある．これについては以下の「微分行列」で考察を加える．

NDSolve`FiniteDifferenceDerivativeFunctionオブジェクトに関する最も重要な情報である微分の階数は出力形式で表示されるが，時には，例えばプログラムで使うために，これや他の情報をNDSolve`FiniteDifferenceDerivativeFunctionから抽出すると便利である．データが保存されている構造はWolfram言語のバージョンによって異なることがあるので，式の一部を使って情報を交換することは勧められない．それよりも，この目的のために設けられたメソッド関数のいずれかを使った方がよい．

NDSolve`FiniteDifferenceDerivativeFunction[data]オブジェクトを FDDF で表すことにする．

NDSolve`FiniteDifferenceDerivativeFunction[data]オブジェクトから情報を抽出するメソッド関数

各次元についての要素のリストを返すメソッド関数はどれも，整数の引数 dim で使うことができ，FDDF@method[dim]=(FDDF@method)[[dim]]のように特定の次元における値だけを返す．

次の例はこれらのメソッドの使い方を示している．

格子点のテンソルの階数はテンソル積の次元よりも1大きい．これは各点を定義している3つの座標がそれ自身リストになっているからである．格子変数に依存する関数がある場合，Apply[f,fddf["Grid"],{n}]を使ってもよい．ここで，n=Length[fddf["DerivativeOrder"]]は微分を近似しようとしている空間の次数である．

上記のように中程度の大きさのテンソル積格子の場合，Applyを使うとかなり速くなる．しかし，ApplyはWolfram言語のコンパイラ，つまりパックアレーでは，限られた方法でしか使うことができないので，格子が大きくなるにつれてこの方法は最速ではなくなる．Applyの代りにMapを使うように関数を定義することができるなら，CompiledFunctionが使えるかもしれない．というのも，MapはApplyよりもWolfram言語のコンパイラでの適応性が高いからである．

関数がListable属性を持っている操作および関数から成り立っている場合は，可能であればこの属性を利用するとさらによいだろう．テンソル積の各格子点での ，， の値を分離するのである．それにはTranspose[fddf["Grid"]],RotateLeft[Range[n+1]]]を使うのが近道である．ここでn=Length[fddf["DerivativeOrder"]]は微分が近似されようとしている空間の次元である．これは各要素の次元に対する値が別々になっている長さ n のリストを返す．属性Listableを使うことで，これに適用された関数は格子に縫い込まれる．

この例から，CompiledFunctionを使った方が一般にApplyよりもはるかに速く，リストできるという特性を利用するとさらに速くなることが分かる．

擬スペクトル法

差分階数の最大値は格子上の点の数で決まる．これを超えると，警告メッセージが表示され，階数は自動的に減らされる．

限定された階数を用いるのは一般に擬スペクトル法と呼ばれる．通常この方法で問題となるのは，人工振動（ルンゲ(Runge)の現象）が極端になる得ることである．しかし，この問題が起らない場合が2つある．ひとつは周期的に繰り返される一様格子の場合で，もうひとつはチェビシェフ(Chebyshev)の多項式 の零点，あるいはチェビシェフ・ガウス・ロバット(Chebyshev–Gauss–Lobatto)点[F96a]，[QV94]に点を持つ格子の場合である．この両者の場合の計算は，高速フーリエ変換を用いて行うことができる．高速フーリエ変換は効率がよく，丸め誤差が最小になる．

"DifferenceOrder"オプションの設定

チェビシェフ・ガウス・ロバット点は の零点である．属性 を使うと，その点を で表示できる．

（一様格子では中央寄りの方が点と点の間隔が狭いので）中央部分の方が近似がうまくいっているようではあるが，このプロットは高すぎる階数での有限差分近似でよく見られる破滅的な振動をよく表している．チェビシェフ・ガウス・ロバット点の間隔を使うとこれが最小限に押さえられる．

周期性があると仮定すると，近似は格段に改善される．周期的な擬スペクトル法による近似の確度は，場合によっては，例えば上記のパルスのようにより大きな計算領域を使って周期性をシミュレートすることで，正当化するに足るだけの高さを持つ．しかしこの近似は，確度は非常に高いが，思いがけない危険を孕んでいないわけではない．最悪の場合は，エリアシング誤差であろう．そうなると，振幅数の大きすぎる振動関数の要素によって近似が阻害されるか，完全に消えてしまうこともある．

有限差分法の精度と収束性

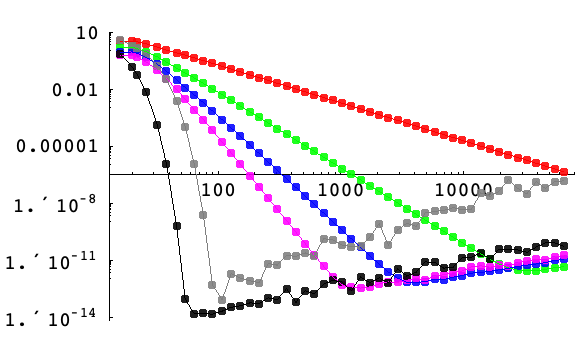
有限差分を使う場合は，打切り誤差，つまりテイラー級数近似を打ち切ることによる漸近的な近似誤差のみが，誤差の原因となるわけではないことを頭に入れておくことが重要である．有限差分式を適用する際に，誤差の原因になるものがこの他にも2つある．それは状態誤差と丸め誤差である[GMW81]．丸め誤差は必要な代数計算における丸めのために起る．状態誤差は，一般に刻み幅のベキ乗による除算によって関数の値中の誤差が拡大されたことによるものであり，刻み幅が小さくなるにつれて拡大する．すなわち，実際には， がゼロに近付くに従って誤差がゼロに近付くとしても，誤差はある点を超えると拡大していくということである．下の図は， が小さくなるにつれて，滑らかな関数が一般的にどのように動作するかを示すものである．

区間を含む格子上の点で機械精度を使って，ガウス関数 の一次導関数を格子点の数 の関数として近似する際の最大誤差の対数プロット．一様格子上の階数2，4，6，8の有限差分がそれぞれ赤，緑，青，ピンクで表示されている．一様（周期的）間隔およびチェビチェフの間隔を使った擬スペクトル法による微分はそれぞれ黒と灰色で表示されている．

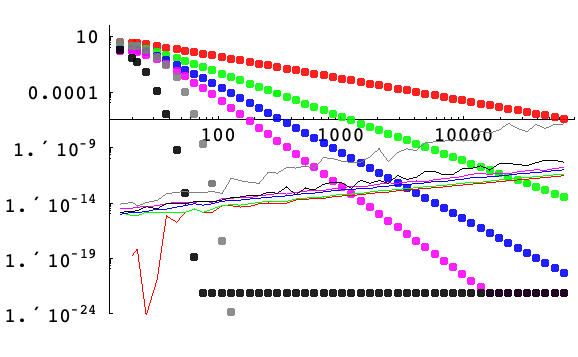
区間を含む格子上の点で，ガウス関数 の一次導関数を格子点の数 の関数として近似する際の打切り誤差（点線）および状態・丸め誤差（実線）の対数プロット．一様格子上の階数2，4，6，8の有限差分がそれぞれ赤，緑，青，ピンクで表示されている．一様（周期的）間隔およびチェビチェフの間隔を使った擬スペクトル法による微分はそれぞれ黒と灰色で表示されている．打切り誤差は高精度で近似を計算することで計算されている．丸め誤差と状況誤差は高精度による近似から機械精度の近似を減算することにより推定されている．丸め誤差と状態誤差は線形に増加し（一次導関数の有限差分式に共通の因子である のため），より高階の微分では少々高めになる傾向がある．擬スペクトル法による微分は，FFT計算の誤差が長さによって変わるのでより変化に富んでいる．一様（周期）擬スペクトル微分の打切り誤差は約以下にはならない点に注意のこと．数学的にいうと，これは，ガウス関数が周期関数ではないからである．この誤差は本質的に周期性からの逸脱を与えるのである．

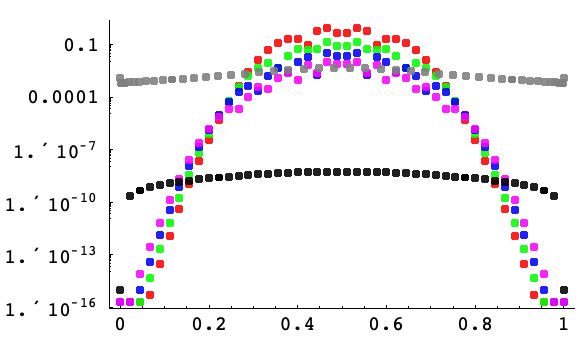
区間における45の格子点上の点で，ガウス関数 の一次導関数を の関数として近似する際の誤差の片対数プロット．一様格子上の階数2，4，6，8の有限差分がそれぞれ赤，緑，青，ピンクで表示されている．一様（周期的）間隔およびチェビチェフの間隔を使った擬スペクトル法による微分はそれぞれ黒と灰色で表示されている．チェビチェフの間隔による擬スペクトル微分以外はすべて一様間隔のを使って計算されている．擬スペクトル微分の誤差がそれほど局所的でないのは明らかである．任意の点における近似は格子全体の値に基づいているので，これは当然である．有限差分近似の誤差は局所化されており，誤差の大きさはガウス関数（片対数プロット上では放物線関数になる）の大きさに従う．

2番目のプロットから，可能な中で最高の微分近似が得られる大きさがあることは明らかである． が大きいと打切り誤差が優勢である． が小さくなると状態誤差と丸め誤差が支配的になる．最適の は高次の微分に対しての方がよりよい近似を与える傾向にある．これは偏微分方程式における空間的離散化では通常問題とならない．というのも，そのレベルの確度まで計算するのは極端に高価だからである．しかし，この誤差バランスは階数の低い差分，例えばヤコビ行列等の近似の際には非常に重要な問題となる．余分な関数の評価を避けるために，通常は一階前進差分が用いられ，誤差バランスは丸めの単位の平方根に比例するようになるので， の値をうまく取ることが重要である[GMW81]．

上記のプロットは，実際の境界効果がない滑らかな関数に典型的に見られる状況を示している．ガウス関数におけるパラメータが変われば関数がより平坦になり，境界効果が現れるようになる．

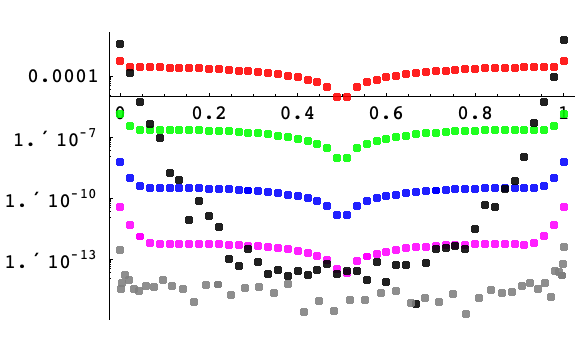
区間における45の格子点上の点で，ガウス関数 の一次導関数をxについての関数として近似する際の誤差の片対数プロット．一様格子上の階数2，4，6，8の有限差分がそれぞれ赤，緑，青，ピンクで表示されている．一様（周期的）間隔およびチェビチェフの間隔を使った擬スペクトル法による微分はそれぞれ黒と灰色で表示されている．チェビチェフの間隔による擬スペクトル微分以外はすべて一様間隔のを使って計算されている．有限差分近似の誤差は局所化され，誤差の大きさはガウス関数の一次導関数に準じている．一様間隔の擬スペクトル（45次多項式）近似の境界付近における誤差は， が小さくなるにつれて非常に大きくなっている．これには限界が設けられていない．一方で，チェビチェフの間隔による擬スペクトルの誤差はより均一で全体として非常に小さい．

ここまで示してきたことから，近似の次数が高ければ高いほど，結果がよくなることが分かる．しかし，他にも2点考慮すべきことがある．ひとつはより高次の近似は関数評価がより高価になるということである．陰的反復が必要な場合（硬い問題におけるように）は，ヤコビの計算がより高価になるだけでなく，行列の固有値もまた大きくなる傾向にあり，結果としてより硬くなり反復型ソルバにとっては解きにくくなる．これは，事実上ヤコビが非零項を持たない擬スペクトル法[F96a]では，極端な例である．もちろん，これらの問題はより小さなシステム（つまり行列）サイズとのトレードオフである．

もうひとつの点は不連続に関連する．一般に，多項式近似は，高次になるほど近似が悪くなる．さらに悪いことには，真の不連続では，格子間隔が小さくなるほど誤差が大きくなる．

区間における128の格子点上の点において，不連続単位ステップ関数 f(x)=UnitStep(x - 1/2)の一次導関数を の関数として近似したプロット．一様格子上の階数2，4，6，8の有限差分がそれぞれ赤，緑，青，ピンクで表示されている．一様（周期的）間隔およびチェビチェフの間隔を使った擬スペクトル法による微分はそれぞれ黒と灰色で表示されている．チェビチェフの間隔による擬スペクトル微分以外はすべて一様間隔のを使って計算されている．すべてに振動が見られる．しかしこの点についてはチェビチェフの擬スペクトル微分が他よりもよいことは明らかである．

既知の不連続については波面追跡法等数多くの代替策がある．一階前進差分は振動を最小化するが，人工的な粘性項を導入してしまう．よい代替案として，いわゆる本質的に振動しない（essentially nonoscillatory，略してENO）スキームが考えられる．これは不連続から階数をすべて取り去り，不連続性の近くに近似の次数と振動動作を限定する限界を導入するというものである．現在のところENOスキームはNDSolveには実装されていない．

結局，適切な差分階数の選択は問題の構造によって変わってくる．デフォルトの4は幅広い偏微分方程式に一般的に当てはまるものであるが，問題によってはよりよい結果を得るために他の設定を試してみた方がよいこともあるだろう．

微分行列

微分は自然な有限差分近似と同様に線形操作であるから，FiniteDifferenceDerivativeFunctionのアクションを表す別の方法は行列である．微分演算子の近似を表す行列は微分行列[F96a]と呼ばれる．微分行列は常に有限差分近似を適用する最適な方法であるとは限らない（特に複雑さや誤差を小さくするためにFFTが使える場合等）が，偏微分方程式を解く際にしばしば必要になる線形ソルバで使う，分析を助けるものとしてかけがえのないものである．

FDDF がNDSolve`FiniteDifferenceDerivativeFunction[data]オブジェクトを表すとする．

微分行列の作成

行列は疎行列で与えられる．というのも，一般に微分行列は非較的少数の非零項しか持たないからである．

先に指摘したように，分析する際には行列という形式が便利である．例えば，直接ソルバで使ったり，線形安定分析等に使える固有値を求めたりするためにも使えるからである．

擬スペクトル微分に関しては，これは高速フーリエ変換を用いて計算することができるが，小さい場合は微分行列を使った方が速いだろう．しかし究極的には，大きな格子上ではより複雑で数値的な特性を持つ高速フーリエ変換の方がよい選択ということになるだろう．

多次元の微分に関しては，一次元微分に対する行列のKroneckerProductである，平坦化したデータに作用するような行列が形成される．これは例題を見るのが一番分かりやすいだろう.

これは および 方向の格子の外積である格子上のガウス関数を評価する：

これは四階差分を使って，関数の混合 - 部分を計算するNDSolve`FiniteDifferenceDerivativeFunctionを定義する：

微分行列が1353×1353行列である点に注目のこと．1353という数はテンソル積行列上の点の総数であり，もちろん 格子と 格子上の点の数の積である．微分行列はテンソル積格子上でデータを平坦化したデータのベクトルに働く．この行列は非常に疎でもある．非零要素は全要素のおよそ0.5%にすぎない．このことは非零の値の位置のプロットから容易に分かる．

これは2つの方法での複合 - 部分の計算を比較する：

この行列はKroneckerProduct，または一次元行列の直接の行列の積である．

微分行列を使うと機械数の値が若干値が異なる．これは操作の順序が異なるために，丸め誤差が異なってくるためである．

導関数の線形結合が望まれている場合，微分行列は有利である．例えば，ラプラス演算子の計算は単一の行列にすることができる．

これは および 方向の微分に関連付けられた微分行列を計算する：

離散化された従属変数の解釈

WhenEventで，StepMonitor等のモニタオプションで，あるいは従属変数の解釈が必要なProjection等のメソッドで，従属変数が常微分方程式に与えられている場合，その解釈は通常明らかである．時間の特定の値（あるいは独立変数）において，その従属変数の解の要素にその値を使う．

偏微分方程式での解釈は，常微分方程式のときほど明確ではない．数学的に言うと，特定の時間における従属変数は，空間の関数である．これで，InterpolatingFunctionを使って，従属変数を空間領域にまたがる近似関数として表すというデフォルトの解釈に帰着する．

偏微分方程式での別の解釈では，特定時間における従属変数を，その時間における空間離散値，つまり時間と空間の両方で離散化された値を表すものと考えることもできる．MethodOfLinesオプションのDiscretizedMonitorVariables->Trueを使うと，モニタとメソッドでこの完全に離散化された解釈が使われるようにすることができる．

以上2つの解釈の違いは，以下の例で見ると明らかであろう．

上記のコマンドを実行すると，StepMonitorのu[t,x]は実質的にxの関数となるため，Plotでプロットすることができる．この関数に数値積分等，他の操作を実行することもできる．

この場合，u[t,x]は，空間格子上で離散化された解の値を持つベクトルとして，各ステップで与えられる．この例では，離散化された点を示すことで，前面が形成されるにつれて，どれほどよく解決されているかを見ることができるため，さらに情報量の多い監視ができる．

値のベクトルには，格子自体に関する情報は含まれていない．この例では，指数値に対するプロットが作成されており，一様格子の正確な間隔が示されている．uが関数と解釈される場合は，格子は空間的な解を表すために使われるInterpolatingFunctionに含まれる．従って，格子が必要な場合には，u[t,x]を表すInterpolatingFunctionから抽出するのが最も簡単である．

最後に，離散化された表現を使うと，格段に速いことを覚えておかなければならない．これはWhenEventの表現やProjection等の解法を使っている場合は特に重要事項であろう．解が計算領域を超えないようにするためにイベント検出が使われる例題では，離散化解釈を使った方が格段に計算速度が速い．

境界条件

偏微分方程式では，特定の方程式および境界条件について，境界条件を適用する数値的な方法を指定することができることが多い．先に「線の方法」導入部分で示した例題がこれに当たる．しかし，一般的なアルゴリズムを見付けることの方がはるかに困難な問題であり，境界条件が硬さや全体的な安定性に影響を与えるために複雑になっている．

周期境界条件は特に扱いやすい．有限差分には周期的な補間が用いられるからである．擬スペクトル法は一様格子において正確なので，解がきわめて効率的に見付かることが多い．

偏微分方程式の境界条件を与える

複数の関数 u₁, u₂, …について解いている場合，その中の任意の関数が周期境界条件を持つためには，すべての関数が周期境界条件を持っていなければならない（条件は1つの関数について指定されればよい）．複数の空間次元を扱っている場合は，周期境界条件を持つことができる独立変数の次元もあるが，持つことができないものもある．

解として返されたInterpolatingFunctionオブジェクトでは，この次元が周期的に反復していることを示すために，{…,x_min,x_max,…}という表記で省略が使用されている．

これで，における周期的連続から導出した解の一部の表面プロットを作成する：

NDSolveは非周期境界条件については2つの方法を用いる．どちらの方法にも　長所と欠点とがある．最初のメソッドは時間変数について境界条件を微分し，その結果得られる微分方程式について境界上で解く方法である．2つ目の方法は，各境界条件をその状態で離散化する方法である．こうすると境界解の構成要素についての代数方程式が得られるのが通例である．このため，方程式は微分代数方程式ソルバで解かれなければならない．これはMethodOfLinesのDifferentiateBoundaryConditionsオプションで制御することができる．

微分法がどのように動作するかを見るためには，もう一度「はじめに」の部分に挙げた線の方法の例題に戻ってみるとよい．最初の公式で，におけるディリクレ(Dirichlet)境界条件が についての微分で処理されている．ノイマン(Neumann)境界条件は反射の概念を用いて処理されている．これは二階有限差分近似については有効であるが，より高階までの一般化ではこれほど容易ではない（しかし，この問題については，反射全体を計算することで簡単に解くことができる）．微分法は におけるノイマン境界条件上におけるあらゆる階数の差分にも使うことができる．例として，この問題の解が四階差分を使って展開できる．

これは のベクトルを定義する：

では，離散化された境界条件は単に となる．方程式を微分し，それを加える：

この方程式の利点は，導関数を含ませることにより明示的にu₀'[t]が使えるということにある．離散化された系を連立常微分方程式として扱うためには，u₀'[t]について解く必要がある．離散化された境界条件に加えることにより，一時的な逸脱や初期条件の不整合があったとしても，この方程式の解だけで正しい境界条件に漸近的に収束する．このことは，厳密な解から見ることができる．

において導出された境界協定式の厳密な一般解を見付ける：

スケール因子の値が，実際の境界条件のこの解に対する収束率を決定する．この因子はNDSolveでオプション設定"DifferentiateBoundaryConditions"->{True,"ScaleFactor"->sf}を使うことで制御することができる．"ScaleFactor"のデフォルトAutomaticでは，ディリクレの境界条件にはスケール因子1が，その他では0が使われる．

これは空間方向の におけるノイマン境界条件を離散化する：

これは離散化された境界条件を について微分し，それを離散化された境界条件の代りに使用する：

技術的には，境界条件の離散化は微分方程式の残りの部分と同じ差分階数で行われる必要はない．事実，片側微分の誤差項の方がはるかに大きいので，境界近くまで次数を上げた方がよいこともある．NDSolveはこれを行わない．なぜなら，差分階数とInterpolatingFunctionの補間階数が空間方向で同じであることが望ましいからである．

これは における境界条件がどのくらい満足されているかのプロットを表示する：

境界条件を代数条件として扱うと，DAEソルバを使ってプロセスが数段階短くなる．

これは における境界条件がいかに満足されているかを表示する：

この例題では，境界条件は両方の場合で許容誤差内で十分に満足されているが，微分法の方が若干よい．しかし，常に微分法の方がよいとは限らない．境界条件が微分される場合，解が実際の境界条件から局所的に離れている場合がある．

これは，におけるディリクレ境界条件が2つのメソッドでどれほど満足されているかを比べるプロットを作成する．微分した境界条件による解は黒で示されている：

NDSolveを使うときはDifferentiateBoundaryConditionsオプションを使って2つのメソッドを簡単に切り換えることができる．DifferentiateBoundaryConditions->Falseとすると積分メソッドをそれほど自由には選べないことに注意のこと．メソッドは微分代数方程式ソルバでなければならない．

偏微分方程式系あるいはより複雑な境界条件を持つ高階の微分系の場合なら，一般にどちらの方法も使うことができる．片端に複数の境界条件がある場合は，内点に何等かの条件を付ける必要があるかもしれない．次は空間的区間の両端にそれぞれ2つの境界条件を持つ偏微分方程式の例である．

空間誤差に関するメッセージの理解については次のセクションで説明する．今のところはメッセージは無視して境界条件について考察する．

4つの境界条件のそれぞれが，の関数としてNDSolveで計算された解をどの程度満足しているかを示す対数プロットを作成する：

境界条件がAccuracyGoalオプションおよびPrecisionGoalオプションで許される許容誤差範囲で十分満足されているのは明らかである．一般に，高階の微分を持つ境界条件は，低階の微分を持つものほどは満足されない．

もとの境界条件を乗算するスケール因子が，空間微分を持つ境界条件ではゼロになるというのには，2つの理由がある．まず，離散化された方程式に対して条件を課すということは，空間近似に過ぎないため，常にできるだけ厳密にそれを強制することは必ずしも理にかなったことではないのである．また，特に高次の空間導関数では，片側の有限微分からの大きい係数が，条件が含まれる場合に不安定性の原因となり得るということもある．上の例では，この現象が 上の境界条件で起きている．

次は4つの境界条件のそれぞれが， の関数としてNDSolveで計算された解をどれほど満足しているかを示す対数プロットを作成する．最後の境界条件の大きさにおける指数関数的成長が，不安定性の象徴であることに注目する：

矛盾した境界条件

指定する境界条件は，初期条件と偏微分方程式のどちらとも矛盾がないようにすることが大切である．矛盾があると，NDSolveは矛盾についての警告メッセージを表示する．メッセージが表示された場合，解は境界条件を満足しないばかりか，最悪の場合，不安定性が現れる可能性がある．

この熱方程式の例では，における境界条件が明らかに初期条件と矛盾している：

以下は，における解のプロットを の関数として表示する．境界条件 は満足されていない：

境界条件が満足されないのは，常微分方程式の積分が指定された初期条件で開始しているからである．境界で微分された方程式は，一旦微分されると になるため，解は正しい境界条件に近付くが積分区間内ではあまり近くならない．

しかし，微分代数方程式ソルバが，この例のように実質的に正確な解へと導く一貫した初期条件を常に見付けるとは限らない．常微分方程式メソッドを使った解法を改善する一つの方法として，"DifferentiateBoundaryConditions"->{True,"ScaleFactor"->sf}の境界条件スケール因子に，デフォルトの1よりも大きい値を使うというものがある．

熱方程式のこの例では， における境界条件は明らかに初期条件と矛盾している：

次は， の関数としての における解と境界条件の値 の差分を示すプロットである．スケール因子が大きくなるにつれて，境界条件が許容範囲内でより速く満足しているのが分かる：

スケール因子が大きくなると，硬さの原因が導入される可能性があるため，ソルバは方程式が積分しにくくなることがある．スケール因子が100の場合の解から，初期遷移が急速に変化しているのが分かる．

この問題を扱うより確実な方法として，たとえ不連続であっても，境界条件に矛盾しない初期条件を与えるということが挙げられる．この場合は単位ステップ関数が必要なことを行う．

空間誤差推定は滑らかさについて想定されるので，一般に，空間誤差推定は不連続な初期条件に満足できない．従って，通常不連続を近似する滑らかな関数を与えるか，空間離散化で使用する点の数を明示的に指定するかして，不連続の影響をどの程度モデル化したいかを決めることが最善である．空間誤差推定と離散化についての詳細は，「空間誤差推定値」で説明する．

一時変数がより高階の微分を持ち，境界条件が2回以上微分されると，より細かい矛盾が生じる．

以下の波動方程式

初期条件は境界条件を満足するので，NDSolveがNDSolve::ibcincメッセージを表示するのは意外であろう．

2つ目の初期条件を について微分して が得られ，2つ目の境界条件を について微分して が得られたとき矛盾が現れる．この2つは において矛盾している．

まれにNDSolveで，実際には矛盾していない境界条件に対して，矛盾があるという警告メッセージNDSolve::ibcincが出されることがある．これはノイマン境界条件の近似における離散化誤差，あるいは空間微分を含む境界条件によって起る．いくつの点で離散化するかを決めるために使われる空間誤差推定（「空間誤差推定値」を参照）は，境界条件ではなく偏微分方程式に基づいているためである．また，境界条件を近似するために使われる片側の有限差分公式は，同次の中心公式より誤差が大きく，境界においてさらに離散化誤差を発生させる．通常これは問題ではないが，これが起る例題を構築することは可能である．

境界条件が矛盾していないとき，この誤差を修正する方法は，NDSolveが細かい空間離散化を使用するよう指定することである．

空間誤差推定値

概要

NDSolveで偏微分方程式を解く場合，使用する空間格子を明示的に与えるか，MinPointsオプションとMaxPointsオプションに等しい値を与えるかして指定していない限り，NDSolveは空間誤差を推定しなければならない．

空間誤差推定は時間をかけて監視され，空間メッシュは解の展開に応じて更新されることが理想的である．格子の適応性の問題は特定の種類の偏微分方程式では難し過ぎて一般的な方法では解かれていない．さらに，局所的な調整等の手法では，メッシュ点の数を変更するために常微分方程式を最初からやり直さなければならないという理由で，線の方法で使うには問題となることがある．線の方法で使えそうな手法として移動メッシュというものがある．しかし現時点ではNDSolveは静的格子を使用している．使用する格子は，初期条件に基づいた先験的な誤差推測に基づいて決められる．時間的区間の終りで，合理的な一貫性についての帰納的なチェックが行われ，チェックに失敗すると警告メッセージが出される．無論，これはごまかすことができるが，実際にはこれが合理的な折衷案を提供する．失敗する原因で最も多いのは，初期条件にあまり変化がなく推定が本質的に無意味な場合である．この場合は自分で適当な格子設定を選ぶ必要がある．

先験的な誤差推定

NDSolveで線の方法を使って偏微分方程式を解く際は，空間格子について適切な判断をしなければならない．NDSolveは初期条件に基づいた（故に先験的）誤差推定を用いてこれを行う．

これについては例題を用いて説明するのが最も分かりやすいだろう．例として周期境界条件を持つ一次元のサイン・ゴードン方程式を考えてみよう．

時間点は常微分方程式法で局所誤差制御に基づいて適応的に選ばれる．NDSolveは97（周期的終点を含むと98）の空間点を使用する．この選択については以下のステップで説明する．

NDSolveの方程式処理の局面で最初に起ることのひとつに，二階（あるいはそれより高階）の時間微分が一階の時間微分しか持たない系によって置換されるということがある．

次の段階は，時間微分について解くことである．

さて，問題はAccuracyGoalとPrecisionGoalで指定された局所誤差の許容範囲内に微分を近似する一様格子の選択にある．この説明のために，デフォルトの"DifferenceOrder" (4)と，デフォルトのAccuracyGoalおよびPrecisionGoal（両方とも偏微分方程式の場合は4）を用いる．離散化の結果生じた常微分方程式系を積分するために用いられたメソッドの誤差推定は，関数の値が十分に正確であるという推定に基づいている．ここにおける推定の目的は，（少なくとも初期条件で）空間誤差と局所的時間誤差とのバランスがある程度取れている空間格子を求めることである．

誤差推定はリチャードソン(Richardson)補外に基づいている．誤差が であり， の異なる値 と でそれぞれ と という近似があることが分かっていれば，実質的に極限 まで外挿して誤差推定を得ることができる．

従って，の誤差は

と推定される．ここで，と は長さが異なるベクトルであり， は関数であるから，適切なノルムを選ぶ必要がある．を選ぶと，両方のベクトルに共通の要素（すべての と1つ置きの の点）についてスケールされたノルムを使うだけでよい．こうすると格子間の補間が全く必要ないので，よい方法だといえる．

一様格子を設定する際に使う指定区間については，関数 を定義することができる． は格子が（ここで ）となるような区間長である．

以下は，サイン・ゴードン方程式での刻み幅 と格子点のリストを の関数として定義する：

指定された格子について，この方程式は有限差分を用いて離散化することができる．これはNDSolve`FiniteDifferenceDerivativeを使って簡単に行える．

次はサイン・ゴードン方程式の右辺の記号的離散化を格子の関数として定義する．これは，リストの と の近似値を与える と の関数を返す．（原則としてこれは一様かどうかに関わらず，どんな格子でも使えるが，以下では一様格子のみを使用するので注意のこと．）

指定された刻み幅と格子で， と の初期条件も離散化することができる．

次は と の初期条件を離散化する関数を定義する．最後の格子点は，周期的連続により最初の格子点と同じものだと考えられるので，削除される：

関心のある数量は，この初期条件での の特定の値に対する右辺の近似である．

の特定の値から始めて， と の点について右辺を生成することで誤差推定を得ることができる．

上述のように， の点を持つ格子上のひとつ置きの点は 点を持つ格子上の点に対応する．従って，話を簡単にするために，両方の格子に共通の点だけを比べるというノルムを使うことができる．目標としているのは絶対的および相対的な許容誤差の基準を究極的に満足することであるので，スケールされたノルムを使うことに問題はない．スケーリングに際し右辺の大きさを考慮することに加え，格子上の対応する要素 と の大きさを考慮することも大切である．右辺の誤差は最終的に と に含まれるからである．

誤差推定で距離が生成されるよう，Richardson補外の公式(3)に従って，これを単にで割る．

これは での誤差推定を計算する．これはスケールされたノルムに基づいているので，結果が1未満なら許容誤差の基準は満足される：

次は上記の関数を統合して，誤差推定を与える関数を の関数として作成する：

目標は，誤差推定が1以下になる（スケールされたノルムに基づいているため）ような の最小値を求めることである．原則として，これに根探索のアルゴリズムを使うことも可能である．しかし は整数でなければならないので，そのようなアルゴリズムを使うとやり過ぎになり，終了条件の調整が必要になるだろう．これより簡単な解決方法は，Richardson補外の公式を使って の適切な値を予測し，適切な が見付かるまでこの予測プロセスを繰り返すことである．

満足すべき条件は

であり，予測は

であるので，以下の投影が可能である．

あるいは， の逆数に比例する について，以下の投影も可能である．

次は上で計算した についての誤差推定に基づく， の予測最適値を計算する：

次は の新しい値についての誤差推定を計算する：

非常に粗い格子に基づく予測は不適切なことがしばしばある．粗い格子は，細かい格子上での誤差の原因になるような解の特徴を完全に見逃してしまうことがある．また，誤差推定は漸近公式に基づいているので，粗い間隔では，たとえ解のすべての特徴がある程度解決されても推定そのものがあまりよくない．

実際，これらの誤差推定の計算はかなり高くつく．また，本当に最適の を求める必要はなく，誤差推定を満足するものを求めればよい．偏微分方程式が展開するにつれてすべてのものが変わり得るので，最初のためだけの最適間隔を求めるために，余計な時間をかける価値はない．簡単な解法として，新しい について，予測公式に1より大きい因数を追加してみることができる．たとえ追加因数があっても，受容可能な値にいたるまでには数回の反復が必要かもしれない．しかし，こうすることで一般にプロセスが速まる．

不連続な初期関数等では誤差の許容度が満足できない可能性があるので，このプロセスは極限値を持たなければならないということに注意することが重要である．NDSolveではMaxStepsオプションが極限を提供する．空間的離散化については，全空間次元で合計1万回までがデフォルトである．

擬スペクトル法による微分は多項式的ではなく指数的に収束するので，この誤差推定を使うことはできない．推定は，既出の公式で極限p->Infinityに基づいて行うことができる．要するに，細かい格子上の結果を厳密であるとし， がに近付いているので誤差推定がその差分に基づいているとすることである．よりよいアプローチは 個の点を持つ指定された格子上では，擬スペクトル法は であるという事実を用いることである．2つの格子を比較する際には， について小さい方の を使うのが適当である．これにより，格子の大きさを決定するのに不完全ではあるが適切な推定が得られる．

同様に， の代りに を用いるように予測の式が修正できる．

次は擬スペクトル法で使えるように， の適当な値を予測する関数を変更する．この公式化は効率的なFFT（高速フーリエ変換）の長さを選ぼうとはしない：

擬スペクトル法の の選択を最終的に行うときに，加えて考慮に入れたいことは，許容条件を満たすのみでなく高速フーリエ変換の計算に十分な長さにもなる値を選ぶことである．Wolfram言語では，Fourierコマンドに素因数アルゴリズムが組み込まれているので，効率的な高速フーリエ変換で2つの長さのベキ乗を必要としない．

一般に，差分階数は誤差推定を満足するのに必要な点の数に大きな影響を与える．

差分階数の関数として必要とされる点の数の表は，線の方法のデフォルト設定が"DifferenceOrder"->4となっている理由を説明するのに役立つ．2から4までの向上が一般に最も劇的で，デフォルトの許容誤差範囲では，四階差分を使うと，より高階ではありがちな大きな丸め誤差を生み出すことはあまりない．擬スペクトル差分を選ぶと，特に周期境界条件のときにうまくいくことがしばしばあるが，完全なヤコビ行列を導くのでデフォルトとしてはあまりよい選択とは言えない．完全なヤコビ行列は，硬い方程式で必要となった場合に，生成して解くのに高くつく．

非周期格子の場合，誤差推定は内点のみを用いて行われる．それは，境界付近の微分の誤差係数が異なるからである．これにより境界付近の特徴が見失われるかもしれないが，偏微分方程式の展開によってすべてが変わり得るので，ここで重要なのは推定が簡単で廉価であることである．

多空間次元については，打切りは一度にひとつの次元について行われる．ある次元でよりうまく解決できれば，それによって他の次元についての必要条件が変わることもあるので，よりよい選択となるようにこのプロセスは逆方向に繰り返される．

帰納的誤差推定

NDSolveで偏微分方程式を解く際の最後のステップは，展開した解に空間誤差推定を行い，それが極端に大きい場合はエラーメッセージを出すことである．

この場合の誤差推定は先述した先験的な推定と同じような方法で行われる．事実上唯一の違いは，誤差の推定に点の数が と の格子を使う代りに，と の格子が使われる点である．これは，点の数が 個の格子では補間を使わない限り値が生成できず，それによる誤差が導入されてしまうが，点の数が の格子なら値をひとつ置きに拾うだけで簡単に値が得られるからである．これはRichardson補外の公式で を使って簡単に行うことができる．結果は次のようになる．

次はベクトルとして表された と についての解から，サイン・ゴードン方程式の解の誤差推定が計算できる（前セクションで定義された関数に基づいた）関数を定義する．この関数はすでに構築されている格子に適用されるので，格子関数として定義されている．（ここで定義されているように，この関数は長さが等しい格子にしか使えない．異なる長さを扱うことも困難ではないが，そうすると関数が少々複雑になる．）

これはの特定の数値における帰納的な誤差推定を与える関数を作成する：

これは帰納的な誤差推定のプロットを の関数として作成する：

この関数に見られるような大きな局所的変化は一般的なものである．この例題では，もとの一つのピークが別々の波に分かれるちょうどそのときに大きいピークが起っている．このため，NDSolveは推定値が10（初期条件に基づいて格子を選択する際に使われる1ではない）を超えない限り，過剰な誤差についての警告は発しない．従って，NDSolveが帰納的な誤差推定に基づいた警告メッセージを発するのは，通常新たな解の特徴が現れたか，解法の過程で不安定性がある場合である．

これは における解のプロットを表示する．頂点近くの振動が物理的なものではないので，明らかに警告メッセージが出されるのが適切である：

NDSolve::eerrというメッセージが表示された場合は，デフォルト設定では正確な解が求まらなかった可能性があるので，オプションを使って格子選択のプロセスを制御する必要があるかもしれない．

空間格子選択の制御

NDSolveでの線の方法の実装には，空間格子の制御の方法が何通りかある．

オプション名	デフォルト値
AccuracyGoal	Automatic	格子間隔を決定するための絶対許容誤差の桁数
PrecisionGoal	Automatic	格子間隔を決定するための相対許容誤差の桁数
"DifferenceOrder"	Automatic	空間離散化に使用する有限差分近似の階数
Coordinates	Automatic	独立変数の次元 に対する各空間次元で使用する座標のリスト．これはこのリストで後続するすべてのオプションの設定に優先する
MinPoints	Automatic	格子の各次元で使用する点の最低数．Automaticの場合の値は，指定された差分階数での誤差推定に必要な最小の点の数となる
MaxPoints	Automatic	格子で使用する最大点数
StartingPoints	Automatic	先験的誤差推定を用いて格子の微調整を始める際の点の数
MinStepSize	Automatic	使用する最小の格子間隔
MaxStepSize	Automatic	使用する最大の格子間隔
StartingStepSize	Automatic	先験的誤差推定を用いて格子の微調整を始める際の格子間隔

線の方法でのテンソル積格子のオプション

テンソル積格子の離散化のためのオプションはすべて，空間次元の数と等しい長さのリストとして与えることができる．この場合，各空間次元のパラメータはリスト中の対応する要素で決定される．

非周期問題で使う擬スペクトル法を除いて，離散化は一様格子を使って行われる．このため，区間長が である問題を解く場合，PointsオプションとStepSizeオプションの間には直接的な対応がある．

StepSizeオプションは実質的に対応するPointsの値に置き換えられる．問題のスペックは離散点の数よりも刻み幅と関連している方が自然なこともあるので，この両者は便宜上与えられているに過ぎない．Pointsおよび対応するStepSizeオプションの両方にAutomatic以外の値が指定されているときは，一般により厳格な制限が使われる．

前のセクションで，展開するにつれて勾配が急になるために解が十分に解けない例を示した．次の例では衝撃波近くがもう少しうまく解決されるように，格子パラメータを別の方法で修正している．

プロファイルが急勾配になるにつれて解に現れる振動を避ける方法のひとつは，プロファイルが最も急なときに分析するために，確実に十分な点を使うということである．バーガーズ方程式の解

において， 衝撃波プロファイルの幅は に従うにつれて に比例する[W76]ということを示している．変化の95%以上が幅 の層に含まれる．このように，プロファイル幅の半分という最大刻み幅を取れば，プロファイルの急勾配になっている部分のどこかに常に点があり，大きな振動なしにこれが解決できる望みがある．

プロファイルだけを解いても，の確度を必要とするNDSolveのデフォルトの許容誤差を満足することにはならない点に注意のこと．しかし，基本的なプロファイルを解くのに十分な数の点があれば，NDSolve::eerrメッセージに示されているように帰納的な誤差推定に基づいて投影するのも不合理ではない（所詮これは単なる投影であるため，この誤差推定には10%の余分を含む）．

このような解を比較するのには，空間格子点のみで解のプロットを見るのが有効である．格子点はInterpolatingFunctionの一部として保存されているので，空間格子点のみで解をプロットする関数を定義するのは比較的簡単である．

次は時間 における空間格子点のみで解をプロットする関数を定義する：

で見付かった3つの解を比較するプロットを作成する：

この例では領域の左側にはさほど多くの点は必要ではない．点が凝集されるのはプロファイルが急傾斜になっているところである．であるから，プロファイルが現れるところで点の数が多くなる格子を明示的に指定するのも理にかなっている．

次は，点のほとんどが の右側にある指定格子のバーガーズ方程式を解く：

同じ原則の多くが多空間次元にも当てはまる．異方性を持つ二次元のバーガーズ方程式がよい例である．

これは と 方向の速度が異なる二次元のバーガーズ方程式の変形を解く：

次は，における解の立ち上がりの表面プロットを表示する：

一次元の場合と同じように，立ち上がりは急勾配になる．粘性項()の方が大きいので，急勾配になる度合いはそれほど極端ではなく，実際のところこのデフォルトによる解が前面をかなりうまく解決している．であるから，デフォルトの許容誤差を満たすように誤差推定から投影することも可能なはずである．簡単なスケールの引数が， 方向のプロファイルの幅が 方向のそれよりも倍だけ狭くなっていることを示している． 方向の刻み幅が， 方向の刻み幅よりこれだけの割合で小さくなっているのはもっともなことである．点の最小数は倍少なくなる．

これは 方向の69の点で行った前の計算の帰納的誤差推定から投影した および 方向の刻み幅を適切に制限して，バーガーズ方程式の二次元変種を解く：

この解の計算にはかなり時間がかかる．この解法には1万8千以上の常微分方程式系を解くことが含まれているので，それも不思議ではない．多くの場合，特に次元が多次元の場合は，デフォルトの許容誤差に達するのは非現実的なので，AccuracyGoalおよび／またはPrecisionGoalを使って許容誤差を適度に小さくする必要がある．それほど厳しくない許容誤差で粗い格子の場合は特に，系が硬くないため，明示的なメソッドを使うことが可能なこともある．明示的なメソッドでは，特に高次の問題で問題の多い数値線形代数を避ける．この例ではMethod->ExplicitRungeKuttaを使っておよそ半分の時間で解を求めている．

これ以外のどの格子オプションも各次元の値を与えるリストとして指定することができる．単一の値のみが与えられている場合は，この値が全空間次元に用いられる．これには2つの例外がある．ひとつは，単一の値が外積における格子点の総数と解釈されるMaxPointsであり，もうひとつは格子の各次元を明示的に指定するる必要のあるCoordinatesである．

帰納的空間誤差推定は，単に空間微分を計算する際の局所誤差の推定にすぎず，指定された解法についての実際の累積空間誤差を反映しないことがあることは留意しておく必要がある．実際の空間誤差の推定を求める方法のにひとつに，異なる空間格子に間に合うように，非常に厳しい許容誤差の解を計算してみることが挙げられる．このやり方を以下で示してみる．単純な一次元バーガーズ方程式を考えてみよう．

以下で，差分階数2, 4, 6,で擬スペクトルのバーガーズ方程式の解を計算するために，{33,65,…,4097}の空間格子点を使って解のリストを計算する．基本的に誤差のすべてが空間的離散化からくるように，一時的な確度と精度の許容誤差は非常に高く設定されている．NDSolveで{t,4,4}と指定すると，における解のみが保存される点に注意のこと．このような予防策を講じておかないと細かい格子（時間ステップが多くかかる）での解が使用可能なメモリを使い尽くしてしまうことがある．それでも解のリストの計算には膨大な時間がかかる：

2つの解があるとすると，この2者の比較が必要になる．解自体にある誤差の原因を除くいかなる原因も排除するためには，補間されたデータを使ってInterpolatingFunctionを作るのが一番である．これは2つの解に共通の点を使って行うことができる．

誤差の一般的な傾向を示したければ（不安性の場合は解が収束しないので，何も推定できない），連続する解のペアの差を比較するとよい．

においてバーガーズ方程式の解を格子点の数の関数として近似したときの，最大空間誤差の対数プロット．一様格子上の階数2，4，6の有限差分がそれぞれ赤，緑，青で示してある．一様（周期）間隔の擬スペクトル微分は黒で示してある．

プロットの左上の部分はプロファイルが十分に解決されていない格子である．このため，差分は単に階数1の大きさである（不安定性がある場合はこれよりはるかに悪くなる）．しかし，振動なしにプロファイルを解決するのに十分な数の点があれば，収束は極めて速くなる．当然のことながら，対数線の傾斜はで，これはNDSolveがデフォルトで使用する差分階数に対応する．使用している格子が漸近的に収束している部分に含まれるほど細かいものであれば，前の2つのセクションにおけるのと同じように，リチャードソン補外を使うことによって，局所誤差ではなく全体的な解に簡単な誤差推定が影響することがある．これに対し，より多くの値を計算しプロットを見ると，漸近的な体制にあるのかどうかがよりよく示される．

プロットから，計算される最高の解は，点の数が2049の擬スペクトル法によるものであることは極めて明白である（空間確度が設定された一時的な許容誤差をはるかに超えてしまうので，これより点の数が多い場合は計算されていない）．この解は，事実上，少なくとも許容誤差程度までは，ほとんど厳密解と同様に扱うことができる．

問題の最高の解き方の観点を得るためには，次のことを行うとよい．まず，求まった，少なくとも妥当な近似である各解を，その解の可能な空間確度に相当するように設定された一時的な許容誤差を使って再計算し，結果の確度を解法の時間の関数としてプロットする．次は（少々複雑ではあるが）そのためのコマンドである．

においてバーガーズ方程式の解を計算時間の関数として近似する場合の誤差の対数プロット．示されている各点は，解を計算するのに使われた空間格子点の数を示している．一様格子上の階数2，4，6の有限差分がそれぞれ赤，青，緑で示されている．一様（周期）間隔の擬スペクトル微分は黒で示されている．擬似スペクトル法のコストは513から1025へと大幅に増加している．これは，メソッドが，離散化により生成された密なヤコビアンで非常に高価な硬いソルバに切り替わったためである．

結果のグラフは，周期的擬スペクトル近似がこの場合のようにうまくいくときは，極めて効果的であることを鮮烈に示している．あるいは，ある点までは差分階数が高ければ高いほど，一般に近似結果もよくなる．これらはすべて，バーガーズ方程式のこの例のような滑らかな問題における特徴である．しかし，極限 の方に向かうと，より高階の解が極めて貧弱なものになる．

注意したい最後の点は，上記のグラフが時間方向についてはAutomaticメソッドを使って計算された点である．この方法は，解の展開によって硬い方法と硬くない方法を使い分けるLSODAを使う．格子が粗ければ，厳密に陽的な方法の方が若干速くなる．擬スペクトル法を除いて，陰的BDFメソッドは格子が細かい場合により速くなる．NDSolveにはこの他にもさまざまなODEメソッドが含まれている．

境界上の誤差

先験的誤差推定は，使われるすべての差分に，使用する点の数を実質的に推定するのに使うことのできる一定した誤差項が含まれているため，計算区域の内部で計算される．境界を推定に含めると，先験的推定が正当化できなくなるほどプロセスを複雑にしてしまう．一般にこのアプローチでは誤差を妥当に制御することができる．しかし，困難になる場合もいくつかある．

時折，境界で使用される片側微分の誤差項が大きいために，NDSolveが境界条件と初期条件の間に，離散化誤差の影響である矛盾を検知することがある．

この場合，完全に右境界におけるより大きな離散化誤差についてのNDSolve::ibcincメッセージが出される．この特定の例題では，この方程式の性質上，余分な誤差はなくなってしまうので問題にはならない．しかし，空間点をあといくつか使ってこのメッセージを消去することも可能である．

これは 方向に最低50の点を使用して，上と同じ方程式の解を計算する：

この他，境界における誤差の問題が離散化に予期せぬ形で影響を与える場合として，周期境界条件が真に周期的ではない関数とともに与えられたために，計算に意図しない不連続が導入された場合がある．

ここでの問題は周期的連続を考慮すると，初期条件が事実上不連続になる点である．

先端部分には常に大きな派生的誤差があるので，NDSolveは先験的な誤差限界を満足するために最大数の点を使うように強制される．さらに悪いことに，極端な変化のために結果の常微分方程式を解くことがより困難になり，結果として解を求める時間が長くなりメモリもたくさん使うことになる．

不連続が実際に意図的なものであれば，関心を持っている不連続の一面を扱うのに十分な空間格子用の点の数あるいは間隔を指定した方がよい．一般に高い確度で不連続をモデル化することは，NDSolveが提供する一般的なメソッドの範疇を超えた特化したメソッドが必要である．

一方，この例題の中で計算区域を小さく取りすぎたために不連続が起ったように，不連続が意図したものでなければ，計算区域を広げるか滑らかにするために区間の間に項を挿入するかすると，大抵の場合は簡単に修正することができる．