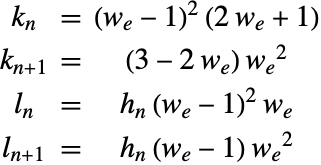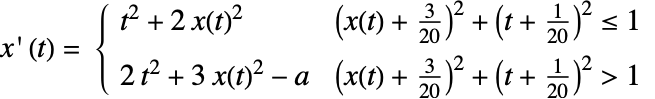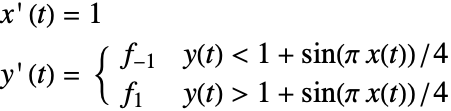微分方程式のイベントと不連続性
はじめに
微分方程式はそれだけで,系の連続的な動作をモデル化するのに非常に効果的である.しかし実数の系の多くには,連続的な解の状態により引き起こされる可能性のある離散時間で変化する要素がかかわっている.例えば,暖房装置の場合,室温がある一定のレベルに達すると温度自動調節器のスイッチが入る.
は,点 ![]() と,ブール値のイベント関数がTrueとなる解である.
と,ブール値のイベント関数がTrueとなる解である.
![]() が
が ![]() のときTrueならば,
のときTrueならば,![]() の値は解の近似と二分法で
の値は解の近似と二分法で ![]() を評価することにより積分中に数値的に見付けることができる.
を評価することにより積分中に数値的に見付けることができる.
一般に,![]() が
が ![]() (
(![]() は実数値の関数)という形式であれば,よりロバストでより速く
は実数値の関数)という形式であれば,よりロバストでより速く ![]() を数値的に見付ける方法が使える.記号処理はイベント式に自動的に実行され,可能ならば実数値関数を得たりより簡単な形式を得たりしようとする.例えば,ブールイベント
を数値的に見付ける方法が使える.記号処理はイベント式に自動的に実行され,可能ならば実数値関数を得たりより簡単な形式を得たりしようとする.例えば,ブールイベント ![]() は,イベントが時間
は,イベントが時間 ![]() で起こりブールイベント
で起こりブールイベント ![]() が実数関数
が実数関数 ![]() に自動的に処理されるように特別に処理される.
に自動的に処理されるように特別に処理される.
不連続の交差等のイベント動作の中には,![]() がFalseで
がFalseで ![]() がTrueとなるような囲い込み区間
がTrueとなるような囲い込み区間 ![]() を見付ける必要があるものがある.また実数値の関数
を見付ける必要があるものがある.また実数値の関数 ![]() の場合,
の場合,![]() と
と ![]() の符号は逆になる.
の符号は逆になる.
イベントの誘引が見付かると,通常何らかの動作が実行される.場合によっては,この動作は,モデリングでイベントを使うことで離散的な動作に対する柔軟性が与えられるよう,積分を中止したり解の変数値を変更したりして,系の積分に影響を及ぼすことがある.
NDSolveでは,イベントはWhenEvent式を持つ微分方程式を拡張する.
このセクションではNDSolveでWhenEventを使った基本的な例題を示す.その後のセクションではイベントの検出と位置特定,状態変数を変更する動作,不連続性の扱い,応用例題等のトピックについて深く掘り下げていく.
簡単な例として,非平衡位置で開始した振子が最低点を通過する時等のイベントを見付けて,その時点で積分を中止するというものがある.
この結果から,振子はおよそ ![]() で最低点
で最低点 ![]() に達することが分かる.InterpolatingFunctionAnatomyパッケージを使うと,InterpolatingFunctionオブジェクトからその値を抽出することができる.
に達することが分かる.InterpolatingFunctionAnatomyパッケージを使うと,InterpolatingFunctionオブジェクトからその値を抽出することができる.
イベントの検出と位置特定
イベントの位置特定は実質的に2段階で行われる.イベント検出の段階では,数値積分メソッドによる各時間刻みについて,その時間刻みの間にそれぞれのイベントが変化したかどうかがテストされる.イベントの可能性が検出されると,位置特定段階では通常根探索手法を使って実際のイベント時間 ![]() を見付ける.
を見付ける.
イベントの検出方法
ある時間刻みの中でイベントが発生したかどうかを検出する最も簡単で速い方法は,イベント関数がFalseからTrueに変化したかどうか,あるいはイベント関数が,符号の変化した実関数の根として表せるかどうかを調べることである.符号だけを使う場合問題になるのは,メソッドが大きなステップを取る場合(外挿メソッドでありがち)や,イベント関数が常微分方程式の解に比べて速く変化する場合に,1つの時間刻みの中で複数の根があってもイベントを見逃してしまう可能性が高いという点である.
実関数の根として表すことのできるイベントの場合,符号を使うという方法はステップの最初と最後にイベント関数の時間微分を含ませることで向上する.イベント関数![]() を持つ常微分方程式
を持つ常微分方程式 ![]() の場合,時間微分は次で簡単に計算できる.
の場合,時間微分は次で簡単に計算できる.
この値は,ステップ区間の中に根があるかどうかをテストする3次エルミート多項式で補間することができる.必要に応じてステップは分割されて,根は根探索手法のために囲み込まれる.
導関数を使うと,![]() が
が ![]() に依存していなければ比較的少ない追加コストで検出をよりロバストなものにすることができる.しかし,このメソッドを使ってもイベントが省略できるという場合もあり得る.
に依存していなければ比較的少ない追加コストで検出をよりロバストなものにすることができる.しかし,このメソッドを使ってもイベントが省略できるという場合もあり得る.
問題によっては,イベントを見過ごされず,NDSolveが非常にロバストな補間を使ったメソッドをサポートするということが確実でなければならないこともあるが,これは非常に高価になる.このメソッドはメソッドからの連続出力あるいは密な出力を使うことを基本として,メソッドと同じ次数のイベント関数の補間式を生成する.補間式は,区間の演算手法を使って時間刻みの中に根あるかどうかがテストされる.
イベント検出の方法は,WhenEventの"EventDetection"オプションで制御される.
| "Sign" | 符号の変化からイベントを検出する |
| "DerivativeSign" | イベント関数の時間微分を追加として使用する |
| "Interpolation" | イベント関数を,メソッドと同じ次数の多項式で補間する |
微分方程式の解自体よりもイベント関数の方が急速に変化する場合,時間刻みにはイベント関数の多数の交差が含まれている可能性がある.これは,上で示したイベントの時間微分の方程式を使って,イベント関数を従属変数として系に入れることで緩和する.これはWhenEventのオプション設定"IntegrateEvent"->Trueを使うと自動的に行われる.
イベントが積分されると,イベントの補間はさらに強力になる.イベント関数の補間式が時間積分メソッドの密な出力の要素にすぎないからである.この場合,補間式の根は高精度メソッドのイベント位置であるため,汎用の根探索メソッドを使う必要がない.このような訳で,"DetectionMethod"->"Interpolation"を指定すると,イベントはデフォルトで積分されるのである.
イベントの位置特定メソッド
一旦イベントが検出されると,次のステップは時間刻みの中でイベントが発生した時間の場所を特定することである.位置を特定するのに使えるメソッドがいくつかある.積分区間の最初と最後で解を取る簡単なものから,イベント値の線形補間や囲い込み根探索法を使うものまである.使用する適切なメソッドは実行速度と位置の正確さの間のトレードオフにより異なる.
位置の特定に使われるメソッドはWhenEventの"LocationMethod"オプションで制御される.
| "Brent" | FindRootをMethod->"Brent"で使ってイベントの位置を探す.これは設定Automaticのときのデフォルトである |
| "BrentBracketRoot" | イベントハンドラに,不連続交差に便利な,調整された根の囲い込みを与える |
| "LinearInterpolation" | 線形補間を使ってイベントの時間を特定してから,三次エルミート補間を使ってイベント時間における解を見付ける |
| "StepBegin" | イベントはステップの最初の解により与えられる |
| "StepEnd" | イベントはステップの最後の解により与えられる |
単独イベントの位置特定は通常非常に早いため,使用されるメソッドにより全体的な計算時間に大きな影響が及ぼされることはない.しかし,イベントが複数回検出されると,位置特定メソッドは大きな影響力を持つ.
"StepBegin"メソッドと"StepEnd"メソッド
イベントの正確な位置は大して問題ではない場合,あるいはイベントの正確な位置が分かっても,内在する計算に確度を持ったものが何も反映されない場合は,最も大雑把なメソッドが適している.
以下の例では,イベントの位置が任意であるため,"StepEnd"が適切である.
この例では,時間刻みが非常に速く計算されるので,特定の時間刻み内で,しかも特定の点ではなおさら,ボタンのクリックにかかる時間を計ることはできない.したがって,イベントの継承された正確さに基づくと,調整する意味がないので,一メソッドの"StepBegin"か"StepEnd"を使うのが最も適している.イベントの定義がヒューリスティックであったり幾分不正確であったりする例題では,この方法が最適である.
"LinearInterpolation"メソッド
グラフにプロットする点のためにイベントの結果が必要な場合は,グラフの解像度に合わせてイベントの位置を見付けるだけでよい.これにはステップの終点を使うだけでは通常大雑把すぎるが,イベント関数の値に基づく単独の線形補間で十分である.
数値積分の連続したメッシュ点におけるイベント関数を以下のように表す.
線形補間は,イベント時間における解の近似にも使うことができる.しかし,導関数値 ![]() および
および ![]() がメッシュ点で利用可能なので,イベントにおける解のよりよい近似は,次のように三次エルミート補間を使って安価に計算することができる.
がメッシュ点で利用可能なので,イベントにおける解のよりよい近似は,次のように三次エルミート補間を使って安価に計算することができる.
設定を"LinearInterpolation"とすると,単独の線形補間に基づく絞込みが指定できる.
周期全体に渡るプロットの解像度において,導関数が軸と交わる正確な点が終点にはならないことは分からない.しかし,十分ズームすると,誤差が見える.
線形補間法は,ポアンカレ断面の計算のように,見ることを目的とするほとんどの場合には十分な方法である.しかし,ブール値を取るイベント関数では,線形補間は実質的には2分法の1ステップでしかないので,線形補間法はグラフィックスには不適切である場合がある.
ブレント(Brent)法
デフォルトの位置特定メソッドは,イベント位置特定メソッドの"Brent"であり,「ブレント法」で記述されているようにFindRootを使ってイベントの位置を見付ける.ブレント法は小区間の根から開始して,補間法と2分法に基づくステップを組み合せることによって,少なくとも二分法と同等の,あるいは多くの場合それよりもよい収束率を保証する.FindRootがイベント関数の根をどの程度の確度・精度で見付けるようにするかは,イベント位置特定メソッドのオプション"Brent"を使って制御することができる.デフォルトは,NDSolveが局所誤差制御で使っているのと同じ確度・精度で根を見付けることである.
イベントが解に依存する場合,微分方程式の ![]() ,引数
,引数 ![]() は時間刻みの中で
は時間刻みの中で ![]() について近似される必要がある.密な出力や難解な出力をサポートするメソッドでは,イベント関数の引数は,連続出力公式を使うことにより非常に効率よく求めることができる.しかし,連続出力をサポートしないメソッドでは,内在するメソッドのステップを取ることで解を計算する必要があるため,比較的高価になる可能性がある.解の近似を求める別の方法で,メソッドの順序通りではないが,NDSolveから返されるInterpolatingFunctionオブジェクトにFindRootを使うことに見合ったものとして,三次エルミート補間がある.これは,ステップの終点における解の値と解の導関数値に基づく補間によって,ステップの中盤で解の近似値を得るものである.
について近似される必要がある.密な出力や難解な出力をサポートするメソッドでは,イベント関数の引数は,連続出力公式を使うことにより非常に効率よく求めることができる.しかし,連続出力をサポートしないメソッドでは,内在するメソッドのステップを取ることで解を計算する必要があるため,比較的高価になる可能性がある.解の近似を求める別の方法で,メソッドの順序通りではないが,NDSolveから返されるInterpolatingFunctionオブジェクトにFindRootを使うことに見合ったものとして,三次エルミート補間がある.これは,ステップの終点における解の値と解の導関数値に基づく補間によって,ステップの中盤で解の近似値を得るものである.
不連続交差を扱うために設定されているイベントの場合,イベントハンドラが不連続の両端で適切な評価を行い,交差が正しく行われることを確実にするために,イベントハンドラが囲い込み区間 ![]() を持っていると便利である.これにはメソッド"BrentBracketRoot"を使う.
を持っていると便利である.これにはメソッド"BrentBracketRoot"を使う.
メソッドオプションは,解の近似およびFindRootの使用を制御する"Brent"と"BrentBracketRoot"に渡すことができる.
オプション名
|
デフォルト値
| |
| "MaxIterations" | 100 | 使用する最大反復回数 |
| "AccuracyGoal" | Automatic | FindRootに渡される目標確度の設定 |
| "PrecisionGoal" | Automatic | FindRootに渡される目標精度の設定 |
| "SolutionApproximation" | Automatic | 調整段階でイベント関数を評価するために解を近似する方法.Automaticか"CubicHermiteInterpolation" |
イベントの位置特定メソッド"Brent"と"BrentBracketRoot"のオプション
AccuracyGoalあるいはPrecisionGoalの設定がAutomaticならば,FindRootに渡される値はNDSolveの局所誤差設定に基づく.
位置特定メソッドの比較
以下の例では,多くの異なるイベント位置特定メソッドで振り子方程式を積分し,イベントが見付かった時間を比較する.
イベントの動作
WhenEvent[event,action]の場合,一旦イベントのトリガポイント ![]() が検出されて解の軌道に沿った位置が見付かると,イベントハンドラはWhenEventの第2引数で与えられる action を評価する.
が検出されて解の軌道に沿った位置が見付かると,イベントハンドラはWhenEventの第2引数で与えられる action を評価する.
まず,一般に時間積分メソッドの密な出力式を使って解の値 ![]() が近似される.常微分方程式の右辺の関数を評価するか,微分代数方程式の密な出力式を使うかして,導関数
が近似される.常微分方程式の右辺の関数を評価するか,微分代数方程式の密な出力式を使うかして,導関数 ![]() が見付けられる.次に,Blockの場合と同様に,時間独立変数が
が見付けられる.次に,Blockの場合と同様に,時間独立変数が ![]() に,従属変数およびその導関数が
に,従属変数およびその導関数が ![]() と
と ![]() の近似値に設定されて式が評価される.評価から返された値がRule,あるいは文字列指示子であれば,イベントハンドラは指定された動作を実行する.
の近似値に設定されて式が評価される.評価から返された値がRule,あるいは文字列指示子であれば,イベントハンドラは指定された動作を実行する.
| "StopIntegration" | |
| "RestartIntegration" | |
| "CrossDiscontinuity" | |
| "CrossSlidingDiscontinuity" | |
| "RemoveEvent" | イベントを削除する |
| y[t]->val | 状態変数 y を val に変更する |
| d[t]->"DiscontinuitySignature" | 不連続シグネチャ変数 d を変更する |
WhenEvent[event,{action1,action2,…}]の場合,actioni は actioni+1が評価される前に完全に評価され処理される.そのため,単独のイベントに対して引き起こされる一連の動作を与えることが可能である.
WhenEventのリファレンスページには,指示子の有無にかかわらずイベント動作の多数の例が挙げてある.ここではイベント順次評価と指示子の扱いを説明する例を取り上げる.
状態変数の変更
一般に,任意のアクション式の評価はNDSolveで使われる解の状態変数に影響を及ぼさない.評価して規則にするWhenEventのアクションを使うことで,離散的なイベント時間で状態を変更させる柔軟な方法が提供される.
この簡単な例は,平坦な表面を跳ねていくボールのモデルである.
規則 x'[t]->-r x[t]は,x[t]0のときは常に状態変数 x′[t]が-r x′[t]で置換されるよう指定する.実質的に新しい解の軌道が計算されているため,変更されたら積分が再開される.
いくつかの状態変数の変更は,変数と値のリストを持つ単独の規則を使うか,複数の規則を使うか指定することができる.以下の例題で示す通り,この2つのアプローチにはわずかに意味的な違いがある.
規則{x[t],y[t]}->{y[t],x[t]}では,右辺が評価されてから対応する状態変数が設定される.アクションが規則のリストであれば,各規則は順に評価される.
2つの規則の場合,まず ![]() が
が ![]() に設定されてから
に設定されてから ![]() が
が ![]() の新しい値に設定される.したがって,2つ目の規則は実際に
の新しい値に設定される.したがって,2つ目の規則は実際に ![]() を
を![]() に設定した効果を持つ.
に設定した効果を持つ.
常微分方程式系 ![]() では,導関数 x'[t]を設定することができない.これらは関数から明示的に決定されるからである.このことは,自動的に一階に簡約される高階の系では,方程式に現れる最高階の導関数は設定できないということを意味する.
では,導関数 x'[t]を設定することができない.これらは関数から明示的に決定されるからである.このことは,自動的に一階に簡約される高階の系では,方程式に現れる最高階の導関数は設定できないということを意味する.

微分代数方程式系 ![]() として解く場合,導関数を設定することは可能である.微分代数方程式の解法プロセスの一部は,残差Gが0になるように矛盾のない値
として解く場合,導関数を設定することは可能である.微分代数方程式の解法プロセスの一部は,残差Gが0になるように矛盾のない値 ![]() および
および ![]() を見付けることである.NDSolveはMethodオプションの設定Method->{"EquationSimplification"->"Residual"}が使われると,方程式を微分代数方程式系として扱うよう指示される.
を見付けることである.NDSolveはMethodオプションの設定Method->{"EquationSimplification"->"Residual"}が使われると,方程式を微分代数方程式系として扱うよう指示される.
形式 ![]() の微分代数方程式として解いているときに,変数またはその導関数が変更されると,与えられた新しい値が
の微分代数方程式として解いているときに,変数またはその導関数が変更されると,与えられた新しい値が ![]() を満足しない限り,
を満足しない限り,![]() となるように変更されなかった変数の値を見付けようとする試みが起こるところで,再初期化が計算されなければならない.この手順と例題の詳細は「イベントを使った微分代数方程式の再初期化」で説明してある.
となるように変更されなかった変数の値を見付けようとする試みが起こるところで,再初期化が計算されなければならない.この手順と例題の詳細は「イベントを使った微分代数方程式の再初期化」で説明してある.
動作が明示的に規則でない場合,その動作は,再編の状態が評価されないように,動作式の中の明示的なRuleすべてのインスタンスを属性HoldFirstを持つ特別なプライベートの頭部で置き換えた後に評価される.戻り値にこの特別な頭部が含まれているなら,状態変化が実行されたことになる.
DiscreteVariablesオプションで指定された離散変数は,規則によってのみ変更できる.離散変数を使う利点は,微分方程式ソルバメソッドが扱える系のサイズを増大しないという点である.これは,ヤコビアンが使われる硬いメソッドでは特に重要である.
イベントと不連続微分方程式
微分方程式系を解くためにNDSolveに組み込まれたメソッドはすべて,微分方程式がいくつかの基本的な連続性条件を満足するという暗示的な仮定に基づいている.常微分方程式の場合,十分条件はリプシッツ連続である.
微分方程式に不連続性がある場合,これらの仮定に違反しており,ソルバは質の悪い解を求める,あるいはまったく解が求められないという場合もある.通常ソルバは,局所的許容誤差を満足しようとして,許容誤差が不連続関数値でさえ満足するほどまでステップサイズを減少させ,見付かった近似でその不連続性を超えて続ける.
上に示されている解は,不連続性の演繹的な知識なく計算され,不連続性の直前の時間刻みへの減少が見られる.不連続性を超えると,時間刻みのサイズは再び大きくなる.実質的にデフォルトのマルチステップ法でも同じことが起こるが,効果を強調するためにこの例題では高階のルンゲクッタ法が選ばれた.
不連続性に遭遇した時間が特定できるなら,近づいてくる側からの値を使って不連続性を設定し,不連続性の反対側の値を使って積分を再開するという方法も取れる.この方法を使うと,極端に小さい時間刻みと潜在的な誤差の両方を避けることができる.
不連続性に遭遇する時間を自然に特定する方法は,イベントを設定することである.Wolfram言語ではWhenEventを使って行うことができる.不連続性の検出にイベントを使う際の問題点の一つは,解に依存するイベントの場合,イベントを正確に位置づけるためにイベント通過後に解を計算しなければならないが,そうするとイベントを設定して避けようとした不連続性を横切る解の近似を含むことになるという点である.NDSolveは,使用中のソルバが平滑な関数をサンプルするように不連続性に遭遇したときにだけ切り替わる不連続性シグネチャ離散変数を使うことでこの問題を解決する.この操作はNDSolveが微分方程式に不連続関数を記号的に検出したときに自動的に行われるが,同じことを実行するWhenEvent式を明示的に設定することもできる.この方法は以下で説明する.
NDSolveが関数の記号形式を見ることができるときは,不連続性を自動的に見付け,イベントを使ってそれを扱うことができる.このアプローチの場合は,時間刻みの数がずっと少なくてすむ.
不連続性がイベントを使って扱われないときは,何倍もの誤差が生じる.
パラメータ ![]() が十分増加すると,通常イベントのない数値法は不連続性を超えて続行することができない.それは不連続性が最初に見付かったとき,反対側の解が不連続性を指し返すからである.
が十分増加すると,通常イベントのない数値法は不連続性を超えて続行することができない.それは不連続性が最初に見付かったとき,反対側の解が不連続性を指し返すからである.
イベントなしの ![]() 数値メソッドは通常不連続性を超えて続行することができない. それは不連続性が最初に見付かったとき,反対側の解が不連続性を指し返すからである.
数値メソッドは通常不連続性を超えて続行することができない. それは不連続性が最初に見付かったとき,反対側の解が不連続性を指し返すからである.
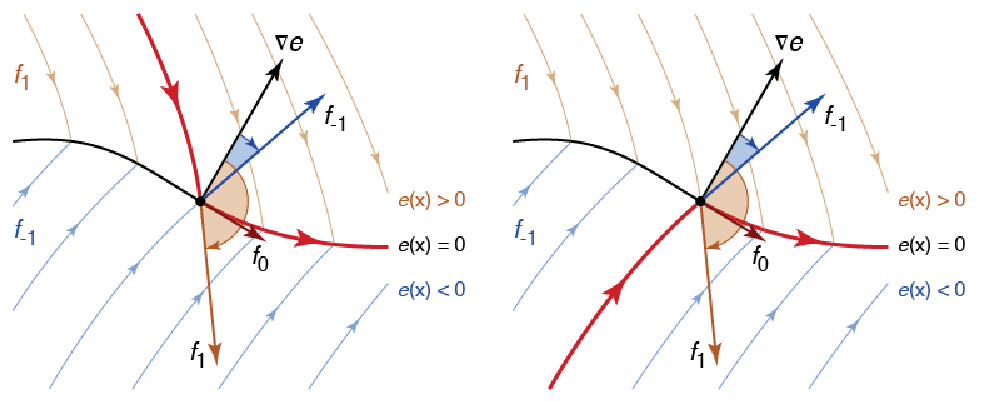
不連続性の記号的検出により,一意な解の存在というWolfram言語の条件に反するとしても,NDSolveはこの場合フィリポフ[F88]のスライディングモードとして知られている連続性を計算することができる.ベクトル場が両側で不連続性に向かっている場合,どちらか片側の場が反対を向くまで連続性は不連続面をすべる.これは上のプロットで見ることができる.ここでは,解はしばらく直接円上にあるが,最終的にそれていく.
次のセクションではフィリポフの連続性と不連続シグネチャの使い方について説明する.
スライディングモード
不連続面が見付かり,その面のどちらかの側のベクトル場が解をさす場合,何かしらの連続法が必要である.連続性がないと,数値メソッドは不連続性を通過し,再び通過するので,通常失敗する.場合によっては数値解は人工的な反跳を示す.
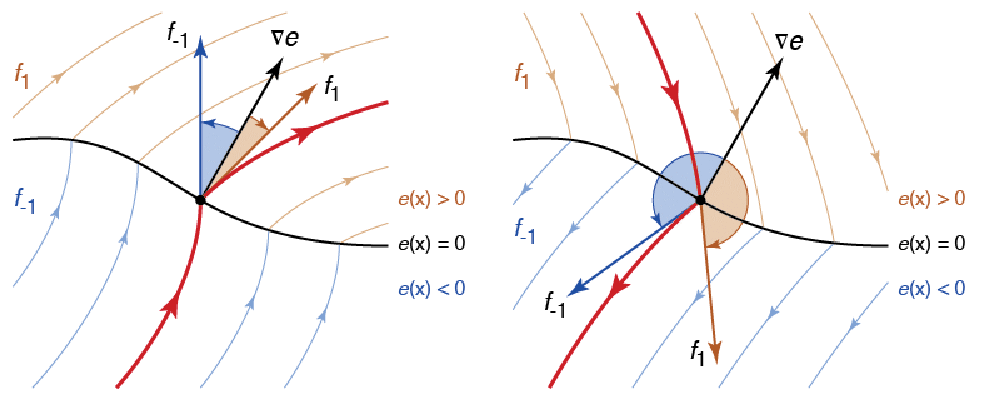
フィリポフ[F88]によって定義された適切な連続性は,不連続面を指すベクトル場の要素の凸結合(あるいは表面が等高線となる関数の勾配ベクトルの対角成分)を取る.
上の図では,不連続面は ![]() によって定義され,
によって定義され,![]() および
および ![]() のベクトル場はそれぞれ
のベクトル場はそれぞれ ![]() と
と ![]() である.曲面上で
である.曲面上で ![]() は
は ![]() を使う.ここで
を使う.ここで ![]() が勾配
が勾配![]() ,特に
,特に ![]() の法線となるよう
の法線となるよう![]() が選ばれる.解左右の図で示されるとおり,上からでも下からでもスライディングモードに入ることができる.
が選ばれる.解左右の図で示されるとおり,上からでも下からでもスライディングモードに入ることができる.
上の定義は,独立変数 ![]() への明示的な依存性がない自律系
への明示的な依存性がない自律系 ![]() に対して与えられる.これと同じ考え方は変数
に対して与えられる.これと同じ考え方は変数 ![]() を加え,自律系
を加え,自律系![]() を考えることによって非自律系
を考えることによって非自律系 ![]() にも当てはまる.
にも当てはまる.
不連続面 ![]() を持つベクトル場
を持つベクトル場![]() によって与えられる簡単な例を見てみる.このベクトル場
によって与えられる簡単な例を見てみる.このベクトル場![]() では,
では,![]() であり
であり ![]() である.したがって,
である.したがって,![]() となるため
となるため ![]() であり,スライディングモードは
であり,スライディングモードは ![]() により支配される.
により支配される.
デフォルトのメソッドは,最終的に不連続性にチャタリングされる小さいステップになるため,止まってしまう.
上の解は正確ではない.スライド面付近の解が大きく振動したりチャタリングしたりしているのは,数値メソッドのアーチファクトである.
不連続関数が方程式の中で明示的なとき,NDSolveはフィリポフ連続を使って自動的に不連続性を扱うことができる.
滑らかな関数が不連続な関数に接近する系のシーケンスを解くことによってスライディングモードの解に近づくので,フィリポフ連続を使うことは当然の選択である.
一般にベクトル場の一つが他方に向くまで,軌道はスライディングモードに囚われる.このようなことが起こると,会は不連続性の上か下で継続することができる.
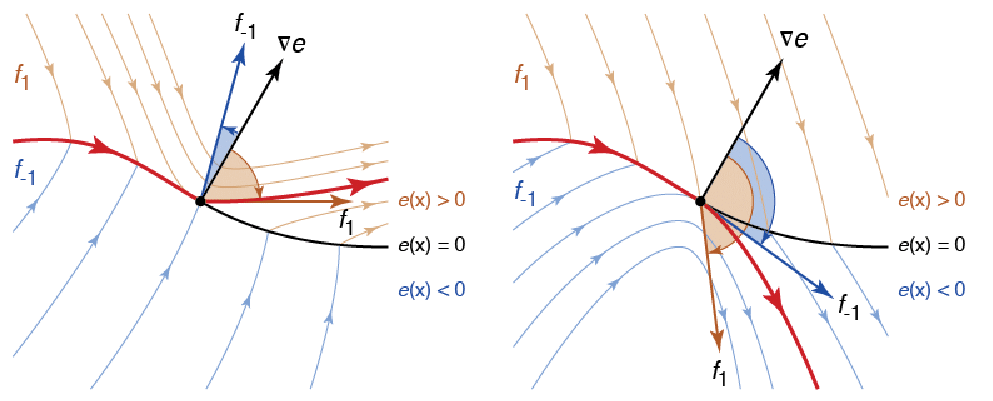
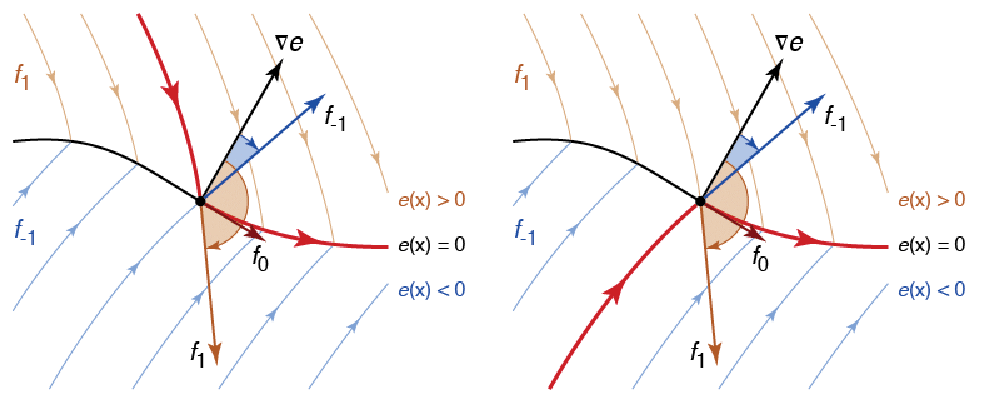
上の図では不連続面が ![]() で定義されており,
で定義されており,![]() と
と ![]() に対するベクトル場はそれぞれ
に対するベクトル場はそれぞれ ![]() と
と ![]() である.曲面上で
である.曲面上で ![]() は
は ![]() を使う.ここで
を使う.ここで![]() は
は ![]() が勾配
が勾配![]() の法線,特に
の法線,特に ![]() になるよう選ばれる.図の両側に示された点を超えると,
になるよう選ばれる.図の両側に示された点を超えると,![]() と
と![]() はともに同じ符合になる.左側は
はともに同じ符合になる.左側は![]() で
で![]() であるため
であるため ![]() となり,右側は
となり,右側は![]() で
で![]() であるため
であるため ![]() となる.どちらの場合も軌道はスライディングモードから出る.これらの点は根
となる.どちらの場合も軌道はスライディングモードから出る.これらの点は根 ![]() または
または ![]() の適切な方を数値的に見付けることで,見付けることができる.
の適切な方を数値的に見付けることで,見付けることができる.
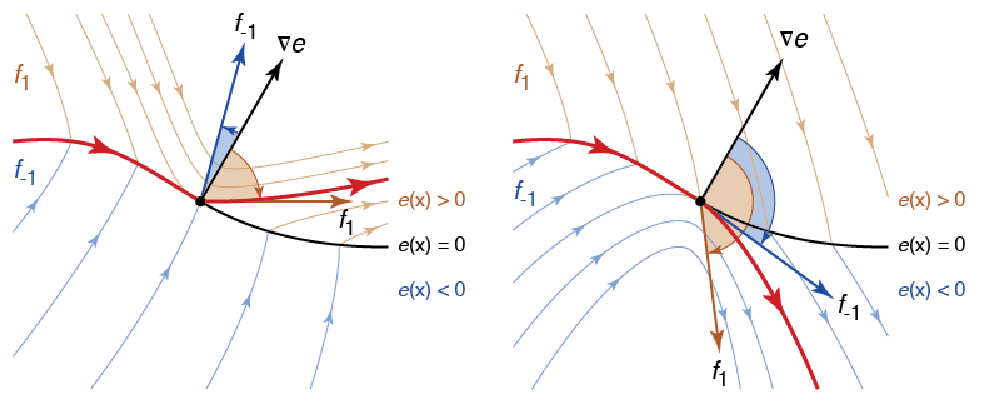
ベクトル場![]() を考えてみる.一旦
を考えてみる.一旦 ![]() となると,下のベクトル場は再び下向きになり,軌道はスライディングモードから逃れることができる.
となると,下のベクトル場は再び下向きになり,軌道はスライディングモードから逃れることができる.
解が繰り返しスライディングモードに入り,スライディングモードから出るということが起こり得る.
ベクトル場![]() を考える.
を考える.![]() のときは,これは負の減衰を持つ振動子に過ぎない.
のときは,これは負の減衰を持つ振動子に過ぎない.![]() のときは,すべての軌道が不連続面
のときは,すべての軌道が不連続面![]() に近づく.
に近づく.![]() のときは,
のときは,![]() が大きすぎなければスライディングモーションのある点集合が存在する.スライディングモーションは実際に負の減衰で起こる無限の成長を安定させるため,周期軌道が存在する.
が大きすぎなければスライディングモーションのある点集合が存在する.スライディングモーションは実際に負の減衰で起こる無限の成長を安定させるため,周期軌道が存在する.
これまで見てきた例題すべては,可視化が簡単という理由で二次元である.しかし連続性は何次元でも動作し,解が一度に2つ以上の不連続面上をスライドするとこに解が発生する.
球面![]() と平面
と平面 ![]() で定義される三次元の不連続面2つと,
で定義される三次元の不連続面2つと,![]() で与えられるベクトル場を考える.
で与えられるベクトル場を考える.
この解はまず球面に沿ってスライドし,両曲面に沿ってスライドし,最終的に平面に沿ってスライドする.
不連続性シグネチャ
不連続性の記号的処理が可能でない等複雑な定義の関数では,NDSolveが不連続関数に対して自動的に行うのと同様の不連続性操作を手動で設定することができる.
不連続性シグネチャ変数は,WhenEvent式を含むことで設定することができる.このWhenEvent式では,イベントが不連続面にあり,アクションが変数を"DiscontinuitySignature"に設定し変数範囲が{-1,0,1}か{-1,1}になるよう指定するDiscreteVariablesオプションを使う規則となっている.
| WhenEvent[e0,s[t]->"DiscontinuitySignature] | s[t]が実質的にSign[e]となるように e によって定義された不連続面の不連続性シグネチャを離散変数 s[t]が持つよう指定する |
| DiscreteVariables->{s[t]∈{-1,0,1}} | s[t]が可能な値-1,0,1を持つ離散変数であることを示す.スライディングモードの解が考慮される |
| DiscreteVariables->{s[t]∈{-1,1}} | s[t]が可能な値-1,1を持つ離散変数であることを示す.スライディングモードの解は考慮されない |
ベクトル場![]() でのスライディングモードに関する前のセクションの最初の例題を考える.
でのスライディングモードに関する前のセクションの最初の例題を考える.
不連続性に遭遇し,解がスライディングモードに入ると,変数 ![]() は
は![]() から0に切り替わる.理想的に,解が厳密に不連続面
から0に切り替わる.理想的に,解が厳密に不連続面 ![]() 上にあると
上にあると![]() は0であるため,スライディングモードは,不連続性シグネチャ0で示される.実際には,数値誤差のために解はこれを満足しないことがある.スライディングモードのとき,NDSolveはできるだけ表面に近くにあるよう試みる.
は0であるため,スライディングモードは,不連続性シグネチャ0で示される.実際には,数値誤差のために解はこれを満足しないことがある.スライディングモードのとき,NDSolveはできるだけ表面に近くにあるよう試みる.
不連続性によってスライディングモードにならないということが分かっているならば,不連続性シグネチャ変数の範囲から0を除くことで必要な計算をあまり高価にしなくてすむ.しかし,これを行っても不連続性でスライディングモードがあると,解は出ないか誤ったものとなる.
によって定義される自律系は ![]() と表すことができる.ここで
と表すことができる.ここで ![]() はNDSolveのWolfram言語式WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"]で設定される.
はNDSolveのWolfram言語式WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"]で設定される.
イベント関数の時間導関数 ![]() は,時間
は,時間 ![]() において
において ![]() のときに何が起こるかを決定するのに重要である.WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"]で
のときに何が起こるかを決定するのに重要である.WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"]で ![]() のときに
のときに ![]() が変化する場合が6つある.
が変化する場合が6つある.
- 場合 3:(上からスライディングモードに入る)
 において
において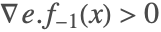 であり
であり 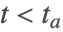 のとき
のとき  および
および  である.
である.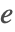 はゼロに向かって減少しているので,
はゼロに向かって減少しているので, では
では  でもある.導関数
でもある.導関数 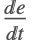 は不連続性の上では負,下では正であるため,軌道は不連続性に囚われる.これはスライディングモードといわれ,
は不連続性の上では負,下では正であるため,軌道は不連続性に囚われる.これはスライディングモードといわれ, の値は0に設定される .事実上のベクトル場
の値は0に設定される .事実上のベクトル場 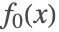 はフィリポフ連続
はフィリポフ連続  (ここで
(ここで 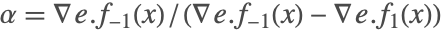 )を使って計算される.
)を使って計算される.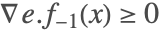 および
および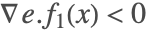 であるため
であるため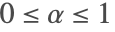 であることに注意する.
であることに注意する.
- 場合 5:(上に向かってスライディングモードから出る)
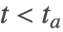 のとき
のとき  .
. ,
,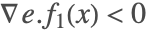 ,
,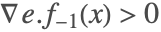 であり,
であり, では
では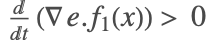 の
の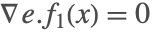 である.解はもはやスライディングモードではなく,
である.解はもはやスライディングモードではなく, は1に設定される.この変化を引き起こすイベントは実質的に
は1に設定される.この変化を引き起こすイベントは実質的に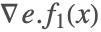 の零交差である点に注意する.
の零交差である点に注意する.
- 場合 6:(下に向かってスライディングモードから出る)
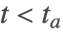 のとき
のとき  .
. ,
,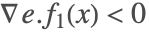 ,
, であり,
であり, では
では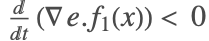 の
の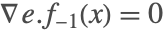 である.解はもはやスライディングモードではなく,
である.解はもはやスライディングモードではなく, は
は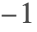 に設定される.この変化を引き起こすイベントは実質的に
に設定される.この変化を引き起こすイベントは実質的に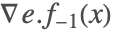 の零交差である点に注意する.
の零交差である点に注意する.
例題
落下する物体
以下の系は空気抵抗を受けた重力のもとで落下する物体をモデル化する([M04]を参照).
ファン・デル・ポル(van der Pol)発振器の周期
ファン・デル・ポル発振器は,極度に硬い常微分方程式系の例である.イベントの位置特定メソッドは,常微分方程式系の積分を実際に行うのにどのようなメソッドを呼び出すこともできる.デフォルトメソッドのAutomaticは必要に応じて硬い系に適したメソッドに切り替えるので,硬さによる問題はない.
NDSolveの解の終点を選ぶことにより,周期を返す関数を ![]() の関数として書くことができる.
の関数として書くことができる.
もちろん,周期解を使ってこのメソッドをすべての系に一般化することは簡単である.
ポアンカレ断面
ポアンカレ断面は,高次元の微分方程式系の解を視覚化するのに便利である.
インタラクティブなグラフィカルインターフェースについては,EquationTrekkerパッケージをご参照いただきたい.
ヘノン–ハイレス(Hénon–Heiles)系
ここでは銀河系の恒星運動をモデル化するヘノン–ハイレス系を定義する.
この場合,関心のあるポアンカレ断面は,軌道が ![]() を通過するときの
を通過するときの ![]() 平面の点の集合である.
平面の点の集合である.
数値積分の実際の結果は必要ではないので,出力変数リスト(NDSolveの第2引数)を空,つまり{}と指定することにより,InterpolatingFunctionにすべてのデータを保存することを避けることができる.こうすると,NDSolveが出力にInterpolatingFunctionを生成しないため,多量の不必要なデータを保存する必要がなくなるのである.NDSolveはNDSolve::nooutというメッセージで出力関数がないという警告を出すが,この場合は必要なデータがイベントアクションから集められているので,メッセージをオフにしても差し支えない.
ここでの計算目的は,比較的低解像度のグラフで結果を見ることにあるため,線形補間によるイベント位置特定メソッドが使われる.ポアンカレ地図の固定点等,詳細を見たり,特徴を調べたりするためにグラフをズームする必要がある例題を行っている場合は,デフォルトの位置特定メソッドを使った方が適切であろう.
ヘノン–ハイレス系はハミルトニアン(Hamiltonian)なので,この例ではシンプレクティック法を使った方が良質な結果が得られる.
ABCフロー
バウンドするボール
この例は,[SGT03]の例題の一般化である.これは,指定された特徴で斜面をバンドしながら降りてゆくボールをモデル化する.この例題は,複数のNDSolveを位置特定メソッドで使って,ある動作をモデル化するよい例である.
偏微分方程式での折返しの回避
多くの発展方程式は,特化された離散化メソッドを使わずに全領域を離散化することができなくなるほどの,無限もしくは十分大きい空間領域上で動作する.実際には,興味のある解が局所化されている限り,小さい計算領域を使うことができる場合もある.
計算領域の境界が,研究中の実際のモデルではなく実践的であるかどうかによって決められている場合,境界条件を適切に選ぶことができる.「擬スペクトル法」で説明してある擬スペクトル法を周期境界条件で使用すると,その優れた近似結果のため,計算領域の範囲を拡張することが可能である.周期境界条件の欠点は,境界を超えて伝播する信号が領域の反対側に残り,折返しによる解への影響が出る.この影響を最小限にするために,境界付近に吸収層を使うこともできるが,常に完全に排除できるというわけではない.
サインゴルドン(Sin-Gordon)方程式は,微分幾何学および相対論的場の理論で現れる.以下の例では,散らばっている局所化された初期条件から始めて,サインゴルドン方程式を積分する.積分には,周期的な擬スペクトル法が使われる.境界付近には吸収層を置いていないので,折返しが顕著になった時点で積分を中止するのが最も妥当である.この条件はWhenEventを使ったイベント位置特定で,簡単に検出できる.
三体問題
この例では,4つの方程式の標準的な硬くないテストシステムである制限三体問題の解を示す.この例は,月の周囲を回って地球に戻る宇宙船の軌道を追跡する([SG75]の246ページを参照).複数イベントおよび零交差の方向が指定できるということが重要である.
最初の2つの解の要素は,無限小量の物体の座標である.従って,ひとつの要素に対して別の要素をプロットすると,物体の軌道が得られる.
遅延のある感染モデル
不連続性シグネチャとCコード
記号的に指定された微分方程式の場合,NDSolveは自動的に方程式をスキャンして不連続関数を見付け,不連続性を適切に扱うためのイベントを設定する.微分方程式系が,記号的にスキャンできない関数評価によって定義されている場合,不連続性シグネチャ変数とイベントを設定し,定義に埋め込まれている可能性のある不連続性を扱う必要がある.
LibraryFunctionを使ってWolfram言語にリンクするようコンパイルされているCで定義された関数は,Wolfram言語が記号的にスキャンできない関数の例である.