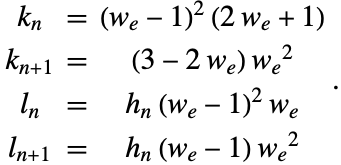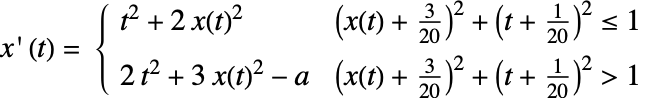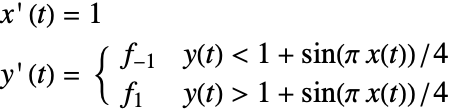微分方程中的事件和不连续性
概述
微分方程本身对于建立系统的连续行为模型非常有效. 然而,许多实际系统,如果包括在离散时间改变的组件,可能由连续解的状态所触发. 例如,在热系统中,一旦温度达到一定值,恒温器就会开启.
是沿着解的一个点 ![]() ,在该点布尔值事件函数变成 True:
,在该点布尔值事件函数变成 True:
当 ![]() 时,
时,![]() 为 True,那么
为 True,那么 ![]() 的值可以通过近似计算
的值可以通过近似计算 ![]() 和使用二分法数值积分得到.
和使用二分法数值积分得到.
通常,如果 ![]() 的形式为
的形式为 ![]() ,其中
,其中 ![]() 是实值函数,那么存在数值求解
是实值函数,那么存在数值求解 ![]() 更有效更快速的方法. 对于事件表达式符号处理是自动进行的,因为它会尽可能地尝试获取实值函数或更简单的形式. 例如,布尔事件
更有效更快速的方法. 对于事件表达式符号处理是自动进行的,因为它会尽可能地尝试获取实值函数或更简单的形式. 例如,布尔事件 ![]() 是被特殊处理的,因此事件会在时间
是被特殊处理的,因此事件会在时间 ![]() 时触发,布尔事件
时触发,布尔事件 ![]() 会被自动处理到实函数
会被自动处理到实函数 ![]() .
.
对于某些事件行为,例如不连续点相交 (discontinuity crossing),有必要找到包围区间 ![]() 使
使 ![]() 为 False 而
为 False 而 ![]() 为 True,或者对于实值函数
为 True,或者对于实值函数 ![]() ,
,![]() 和
和 ![]() 的符号相反.
的符号相反.
当找到事件触发器时,通常会执行某些行为. 在某些情况下,这种行为会通过停止积分或者改变解变量的数值影响系统的积分,因此在建模过程中使用事件对离散行为给出了相当大的灵活性.
在 NDSolve 中,事件参数包含在使用 WhenEvent 表达式的微分方程中.
本章节将介绍在 NDSolve 中使用 WhenEvent 的基本例子. 教程中接下来的章节将深入介绍包括事件检测和定位、修改状态变量的行为、不连续性处理和应用示例等主题.
一个简单的例子是定位一个事件,比如从一个非平衡位置开始的钟摆,何时通过其最低点,并将在该点停止积分.
从该解,用户可以看到钟摆在大约 ![]() 时到达最低点
时到达最低点 ![]() . 使用 InterpolatingFunctionAnatomy 程序包,就可能从 InterpolatingFunction 对象提取值.
. 使用 InterpolatingFunctionAnatomy 程序包,就可能从 InterpolatingFunction 对象提取值.
事件检测和定位
事件定位实际上分两个阶段完成. 在事件检测阶段,对于数值积分方法的每个时间步骤,检测每个事件,以查看是否在步骤中它已经发生改变. 一旦检测到可能的事件,定位阶段通常使用一个求根过程来找到实际事件时间 ![]() .
.
事件检测方法
检测事件是否在时间阶段发送最简单最快的方法是检查事件函数中从 False 到 True 的变化,或者它是否可以表示成实函数的根,一个符号改变.
只使用符号的问题是如果方法花了太大的步骤(例如外插方法通常就会这样)或者事件函数比起常微分方程的解变化太快,很可能会错过在时间步骤中出现两个或者多个根的事件.
对于可以表示为实函数的根的事件,使用符号的方法可以通过在步骤开始和结尾包含事件函数的时间导数增强. 对于常微分方程 ![]() ,其中有事件函数
,其中有事件函数 ![]() ,时间导数可以按以下方法计算
,时间导数可以按以下方法计算
数值可以用立方埃尔米特多项式插值,用于测试在步骤区间是否存在根. 如果需要,该步阶被进一步细分,以使根被包围以完成寻根过程.
使用导数使得检测过程只需一点点额外代价而更加具有鲁棒性,如果 ![]() 不依赖于
不依赖于 ![]() 因此这是这些情况的默认方法. 但是,完全有可能使用该方法,事件被忽略.
因此这是这些情况的默认方法. 但是,完全有可能使用该方法,事件被忽略.
对于某些问题,重要的是确保没有忽略事件,而 NDSolve 支持使用非常具有鲁棒性的插值方法,但是代价明显更高. 该方法基于来自方法的 连续或稠密输出,用于创建与方法具有相同阶数的事件函数的差值. 在时间步骤的根中,使用区间算术技术对插值进行检验.
事件检测方法由 WhenEvent 的 "EventDetection" 选项控制.
当事件函数比微分方程本身的解变化速度更快时,时间步骤可能包括事件函数的许多交叉点. 这可以通过使用上面所示的事件的时间导数的方程,将系统中的事件函数作为应变量缓解. 这可以使用 WhenEvent 中的选项设置 "IntegrateEvent"->True 自动完成.
当事件求积分时,事件插值更具鲁棒性,因为事件函数插值只是时间积分方法的稠密输出的一个分量. 在这种情况下,事件位置处的插值的根是满足方法的完全准确度的事件位置,因此无需使用普通的寻根方法. 为了这个原因,设置 "DetectionMethod"->"Interpolation" 下,默认情况下,事件被积分.
事件定位方法
一旦检测到一个事件,下一个任务就是在事件发生的时间步骤内细化时间位置. 有几种不同方法可用于细化位置. 这些包括简单地在积分区间开始和结尾处取解、事件时间的线性插值和使用包围的寻根方法. 所使用的恰当方法取决于执行速度和位置准确度之间的权衡.
用于修改位置的方法由 WhenEvent 的 "LocationMethod" 选项控制.
| "Brent" | 在 Method->"Brent" 下使用 FindRoot 定位事件;这在设置 Automatic 下是默认的 |
| "BrentBracketRoot" | 对事件处理器给出用于根的修正包围,这对用不连续交叉是有用的 |
| "LinearInterpolation" | 使用线性插值定位事件时间;三次埃尔米特插值,用于在事件时间找到解 |
| "StepBegin" | 事件在步骤开头由解给出 |
| "StepEnd" | 事件在步骤最后由解给出 |
单个事件的定位通常足够快,因此所使用的方法将不会显著影响整体计算时间. 但是,当多次检测到一个事件,定位修正方法可以有实质性影响.
“StepBegin” 和 “StepEnd” 方法
当事件定位的精确位置并不重要、或者不反映底层计算的任何精度信息时,适用粗略的方法.
下面的例子中 "StepEnd" 是合适的,因为事件位置是任意的.
在本例中,时间步进的计算如此之快,以至于无法在一个特定的时间步进内对按钮的点击计时,更不用说在某一时间步进内的一个特定点. 因此,基于事件本身的准确程度,细化没有任何意义. 用户可以通过使用 "StepBegin" 或者 "StepEnd" 定位方法对此进行指定. 在事件的定义是试探性的或者不够确切的任何例子中,这是个合适的选择.
“LinearInterpolation” 方法
当事件结果用于图形绘制中的点的时候,用户只需要把该事件定位到图形的分辨率上. 虽然仅使用步进端点过于草率,基于事件函数值的单一线性插值就足够了.
线性插值也可以用来近似事件时间上的解. 但是,由于导数值 ![]() 和
和 ![]() 在网点是可用的,事件上的解的更好的近似可以廉价地使用三次厄米(Hermite)插值计算:
在网点是可用的,事件上的解的更好的近似可以廉价地使用三次厄米(Hermite)插值计算:
用户可以指定基于具有设置 "LinearInterpolation" 的单一线性插值的细化方法.
在整个周期内的图像的分辨率上,用户看不出端点可能不是确切位于导数与轴相交的位置. 但是,如果充分放大的话,用户就可以看到误差.
线性插值方法对于大部分图示目的是足够的,例如接下来的章节中所示的庞加莱截面的例子. 请注意,对于布尔值事件函数,线性插值实际上只是一个二分步骤,所以线性插值方法可能对于图形是不足的.
Brent 方法
默认的定位方法是事件定位方法 "Brent",即使用带有 布伦特方法 的 FindRoot 寻找事件的位置. 布伦特方法始于一个带括号的根,并且把基于插值法和二分法的步骤结合起来,确保收敛速度至少与二分法一样好,并且大多数情况下更好. 用户可以使用 "Brent" 事件定位方法的方法选项来控制 FindRoot 试图获取的事件函数的根的准确度和精度. 默认情况下是采用与 NDSolve 用于局部误差控制相同的准确度和精度来求得根.
当事件依赖微分方程的解 ![]() ,参数
,参数 ![]() 需要在时间步长内逼近
需要在时间步长内逼近 ![]() . 对于支持连续或者稠密输出的方法,事件函数的变量可以通过使用连续输出公式很有效很简单地找到. 不过,对于不支持连续输出的方法,解需要执行一步底层方法来计算,这样做的代价可能相对比较昂贵. 另外一种获取准确度不及方法的阶数、但与将 FindRoot 用于从 NDSolve 返回的 InterpolatingFunction 对象一致的近似解的方法是,使用三次厄米(Hermite)插值,通过基于在步骤结束时的解的值和解的导数值的插值方法获取步骤中间的解的近似值.
. 对于支持连续或者稠密输出的方法,事件函数的变量可以通过使用连续输出公式很有效很简单地找到. 不过,对于不支持连续输出的方法,解需要执行一步底层方法来计算,这样做的代价可能相对比较昂贵. 另外一种获取准确度不及方法的阶数、但与将 FindRoot 用于从 NDSolve 返回的 InterpolatingFunction 对象一致的近似解的方法是,使用三次厄米(Hermite)插值,通过基于在步骤结束时的解的值和解的导数值的插值方法获取步骤中间的解的近似值.
对于用来处理不连续性交叉点的事件,事件处理器有一个包围区间 ![]() 是很有用的,这使它能够在不连续点的两边都能进行恰当的计算,并且确保正确完成相交(crossing)过程. 这使用方法 "BrentBracketRoot" 完成.
是很有用的,这使它能够在不连续点的两边都能进行恰当的计算,并且确保正确完成相交(crossing)过程. 这使用方法 "BrentBracketRoot" 完成.
可以传递给 "Brent" 和 "BrentBracketRoot" 方法的方法选项控制解的近似和 FindRoot 的使用.
选项名 | 默认值 | |
| "MaxIterations" | 100 | 使用的最大迭代数 |
| "AccuracyGoal" | Automatic | 传递给 FindRoot 的准确度目标设置 |
| "PrecisionGoal" | Automatic | 传递给 FindRoot 的精确度目标设置 |
| "SolutionApproximation" | Automatic | 在修正过程中如何对解求近似以计算事件函数;可以是 Automatic 或 "CubicHermiteInterpolation" |
事件定位方法 "Brent" 和 "BrentBracketRoot" 的选项.
如果 AccuracyGoal 或 PrecisionGoal 的设置是 Automatic,传给 FindRoot 的值是基于 NDSolve 的局部错误设置.
定位方法比较
这个例子使用数个不同的事件定位方法对钟摆方程进行积分,并且比较事件被发现的时间.
事件行为
设置 WhenEvent[event,action] 下,一旦检测到事件触发点 ![]() ,并且它位于解的轨迹上,那么事件处理器计算 WhenEvent 的第二个参数中给出的 action.
,并且它位于解的轨迹上,那么事件处理器计算 WhenEvent 的第二个参数中给出的 action.
首先,对解的值 ![]() 求近似,通常使用时间积分方法的稠密输出公式. 通过计算常微分方程的右边或者使用微分代数方程的稠密输出公司求导数
求近似,通常使用时间积分方法的稠密输出公式. 通过计算常微分方程的右边或者使用微分代数方程的稠密输出公司求导数 ![]() . 那么(在与 Block 相似的方法中)时间无关的变量设为
. 那么(在与 Block 相似的方法中)时间无关的变量设为 ![]() 而应变量和它们的导数在
而应变量和它们的导数在 ![]() 和
和 ![]() 中设为近似值,而且计算该表达式. 如果从计算返回的值是 Rule 或者字符串指令,那么事件处理器将执行指令行为.
中设为近似值,而且计算该表达式. 如果从计算返回的值是 Rule 或者字符串指令,那么事件处理器将执行指令行为.
| "StopIntegration" | 停止 |
| "RestartIntegration" | 重新开始 |
| "CrossDiscontinuity" | 积分到 |
| "CrossSlidingDiscontinuity" | 积分到 |
| "RemoveEvent" | 删除事件 |
| y[t]->val | 把状态变量 y 改为 val |
| d[t]->"DiscontinuitySignature" | 改变不连续性特征变量 d |
设置 WhenEvent[event,{action1,action2,…}] 下,在计算 actioni+1 前在完全计算并且处理好 actioni,因此有可能给出触发单个事件的行为序列.
在 WhenEvent 参考页面中存在许多有和没有指令的事件行为示例. 这里将给出一些示例,演示顺序计算和指令处理.
改变状态变量
一般来说,任意行为表达式的计算不会影响 NDSolve 使用的解状态变量. 使用 WhenEvent 中计算为规则的行为,为在离散事件时间改变状态提供一个灵活的方式.
规则 x'[t]->-r x[t] 指明当 x[t]0 时,状态变量 x′[t] 会被 -r x′[t] 取代. 改变后,积分重新开始,因为实际上在计算一个新的解迹.
多个状态变量的变化可以用带有变量和值的列表的单个规则或多个规则指定. 两种方法有细微的语义差别,详见下例.
在规则 {x[t],y[t]}->{y[t],x[t]} 中,右手边被计算,然后设置对应的状态变量. 当行为是规则列表时,依此计算每个规则.
使用这两个规则,首先,设置 ![]() 为
为 ![]() ,然后设置
,然后设置 ![]() 为
为 ![]() 的新值,因此第二个规则实际设置
的新值,因此第二个规则实际设置 ![]() 为
为 ![]() .
.
对于 ODE 方程组 ![]() ,不可能设置导数 x'[t],因为它们是由函数显式确定的. 对于更高阶方程组,会自动简化为一阶,这意味着出现在方程组中的最高阶导数不能被设定.
,不可能设置导数 x'[t],因为它们是由函数显式确定的. 对于更高阶方程组,会自动简化为一阶,这意味着出现在方程组中的最高阶导数不能被设定.
当作为微分代数方程组 ![]() 来求解时,有可能设置导数. 求解 DAE 过程的一部分是找到
来求解时,有可能设置导数. 求解 DAE 过程的一部分是找到 ![]() 和
和 ![]() 一致的值,使得残差
一致的值,使得残差 ![]() 为 0. 如果使用 Method 选项设置 Method->{"EquationSimplification"->"Residual"} 会使 NDSolve 把方程组作为 DAE 方程组.
为 0. 如果使用 Method 选项设置 Method->{"EquationSimplification"->"Residual"} 会使 NDSolve 把方程组作为 DAE 方程组.
当按 DAE 形式 ![]() 求解时,变量或导数变化时,除非给定的新值满足
求解时,变量或导数变化时,除非给定的新值满足 ![]() ,否则当尝试找到没有变化的变量值时需要重新初始化,使得
,否则当尝试找到没有变化的变量值时需要重新初始化,使得 ![]() . 详细的过程和例子请参见“具有事件的微分代数方程重新初始化”.
. 详细的过程和例子请参见“具有事件的微分代数方程重新初始化”.
当行为不是一个明显规则时,在带有属性 HoldFirst 的特殊私用标头的行为表达式中替代所有显式 Rule 之后计算行为,因此左手边的状态不被计算. 如果返回值具有该特殊标头,然后执行状态改变.
由 DiscreteVariables 选项指定的离散变量只能通过规则改变. 使用离散变量的优点是它们没有增加微分方程求解器方法所使用的系统规模,这对于使用雅可比的刚性方法尤其重要.
事件和不连续微分方程
NDSolve 中求解微分方程的方法是有效地基于隐式假设:微分方程满足某些基本的连续条件. 对于 ODE,充分条件是 Lipschitz 连续性.
当微分方程具有不连续性时,这些假设就不成立,求解器可能给出质量差的解,或者,在某种情况下,可能找不到解. 通常,在尝试满足局部误差容差时,求解器会减小步长直到误差容差甚至满足不连续的函数值,求解器会继续,甚至超出找到的近似不连续性.
这里显示的解是在没有不连续性先验知识的情况下计算的,可以看见时间步长的约简正好在不连续之前. 一旦跨过不连续性,时间步长又增加了. 对于默认的方法(多步长),本质上是进行同样的过程,但是在这个例子中,选择更高阶的龙格-库塔方法以强调效果.
如果可以识别发生不连续性的时间,那么处理不连续性的另一种方法是使用接近端的值步入不连续,然后使用不连续性的另一端值重新积分. 这样可以避免非常小的时间步长和可能的误差.
识别发生不连续的时间的自然方法是设置一个事件. 在 Wolfram 语言中,这可以用 WhenEvent 完成. 使用事件检测不连续性的一个问题是,对于依赖于解的事件,解需要在事件之后计算才可以正确定位事件,但是这会涉及到在整个不连续性中解的逼近,首先要设置事件以避免这种情况发生. NDSolve 通过使用不连续符号差离散变量来避免这种问题,它们只是在发生不连续性时进行切换,因此求解器可高效地采样平滑函数. 当 NDSolve 在微分方程中符号式检测不连续函数时,它可以自动完成这项功能,但是它也可以明确设置 WhenEvent 表达式来完成同样的事情;详细描述如下.
当 NDSolve 可以看见函数的符号形式,它可以自动识别不连续性并按事件处理. 这种方法需要少得多的时间步骤.
当参数 ![]() 充分增加时,没有事件的数值方法一般不能连续通过不连续性,因为,当第一次遇到不连续性时,两边的解会指回不连续处.
充分增加时,没有事件的数值方法一般不能连续通过不连续性,因为,当第一次遇到不连续性时,两边的解会指回不连续处.
当 ![]() ,没有事件的数值方法一般不能连续通过不连续性,因为当首次遇到不连续性时,两边的解会指向不连续处.
,没有事件的数值方法一般不能连续通过不连续性,因为当首次遇到不连续性时,两边的解会指向不连续处.
使用不连续性的符号检测,虽然 Wolfram 语言条件违背解的唯一存在性,但是在这种情况下,NDSolve 可以计算称为菲利波夫(Filippov)[F88] 滑动模式的连续性. 当矢量场的点在两边指向不连续处,连续性有效地沿不连续曲面滑动,直到一边或另一边的场偏离. 在上图可以看出,某段时间解直接在圆上,但是最终偏离了.
该教程的下面章节解释了菲利波夫(Filippov)的连续性以及如何使用不连续符号差.
滑动模式
当遇到非连续曲面,两边的矢量场指回解,使用某种连续方法是必要的. 没有连续性,数值方法在尝试采取步骤跨越和重新跨越不连续性时一般会失败;在某种情况下,数值解会显示人造抖动.
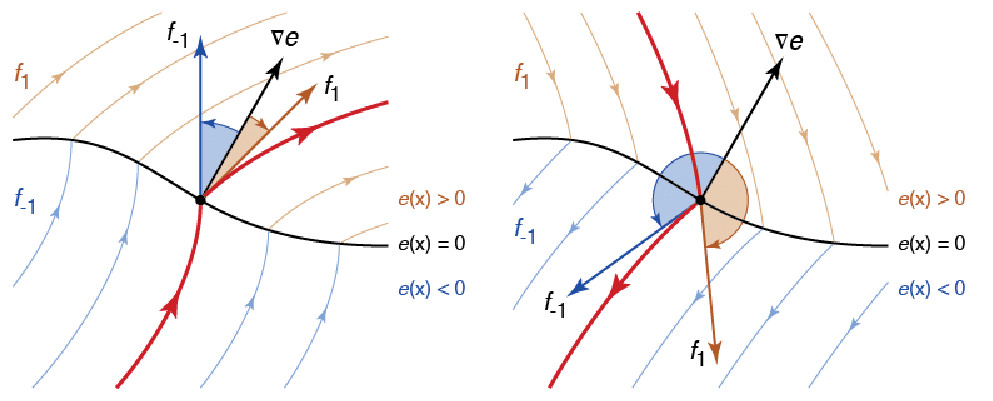
由 Filippov [F88] 定义的恰当连续性有效地采取矢量场组件的凸组合指向非连续曲面(或正交于曲面是阶层曲线的函数的梯度矢量).
在上图中,非连续曲面由 ![]() 定义,对于矢量场
定义,对于矢量场 ![]() 和
和 ![]() 分别为
分别为 ![]() 和
和 ![]() . 然后在曲面
. 然后在曲面 ![]() 使用
使用 ![]() ,其中选择
,其中选择 ![]() ,使得
,使得 ![]() 垂直于梯度
垂直于梯度 ![]() ,特别是
,特别是 ![]() . 解可以从上或下进入滑动模式,分别如图的左右部分所示.
. 解可以从上或下进入滑动模式,分别如图的左右部分所示.
前面的定义是对于自主系统 ![]() ,对于独立变量
,对于独立变量 ![]() 没有明确的依赖性. 同样的方法可以适用于非自主系统
没有明确的依赖性. 同样的方法可以适用于非自主系统 ![]() ,通过增加一个变量
,通过增加一个变量 ![]() 且考虑自主系统
且考虑自主系统 ![]() .
.
一个简单例子是,矢量场为 ![]() 且具有非连续曲面
且具有非连续曲面 ![]() . 如果矢量场为
. 如果矢量场为 ![]() ,
,![]() 和
和 ![]() ;那么
;那么 ![]() ,所以
,所以 ![]() ,滑动运动由
,滑动运动由 ![]() 掌控.
掌控.
默认方法被卡住,因为它最终使用微小的步长使得在非连续处有抖动.
上面的解是不正确的;靠近滑动曲面解的更大振动或抖动是数值法人为造成的.
当非连续函数在方程组中是显式的,NDSolve 可以通过使用 Filippov 连续性自动处理非连续性.
Filippov 连续性是一个自然的选择,因为求解用平滑函数接近非连续的系统序列接近滑动模式解.
一般来说,在滑动模式中迹会被截断直到矢量场偏离. 当这种情况发生时,解会继续在非连续处之上或之下.
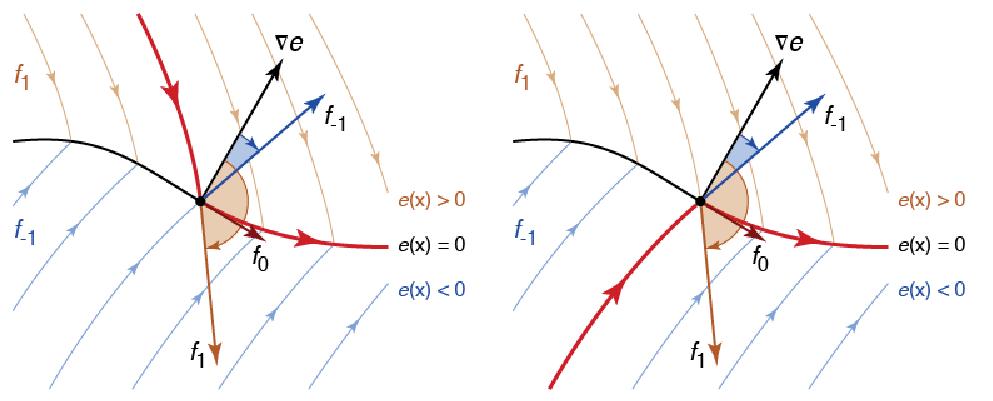
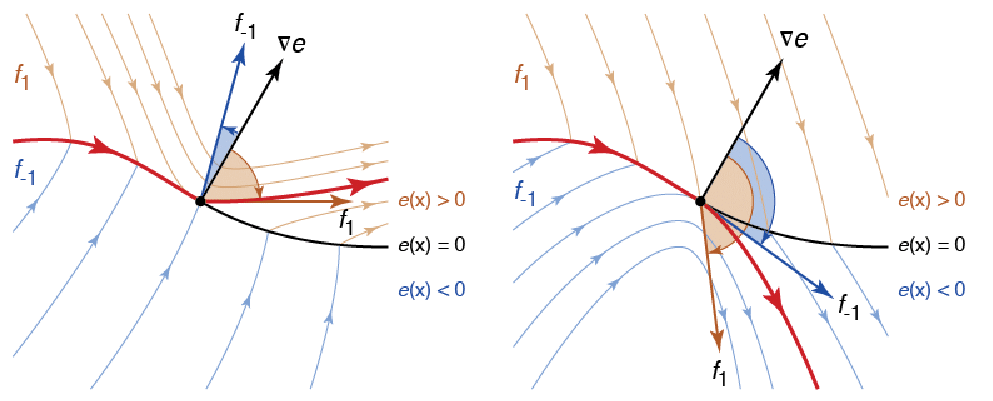
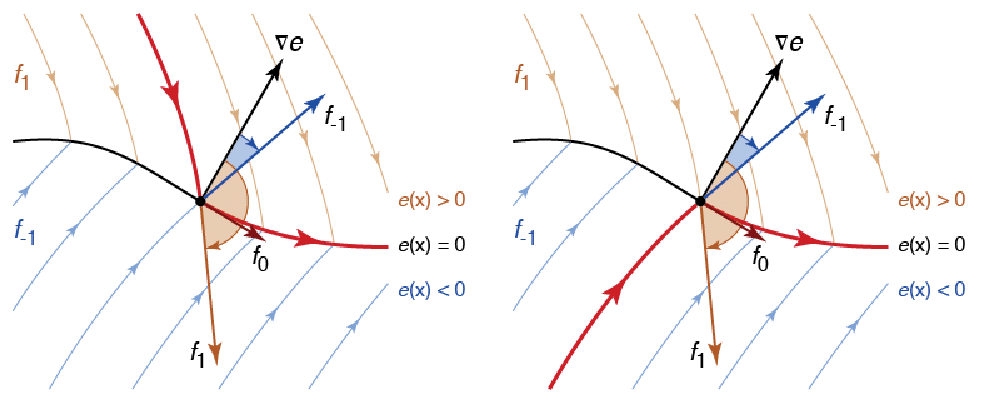
在上面的图中,非连续曲面由 ![]() 定义,对于
定义,对于 ![]() 和
和 ![]() 的矢量场分别为
的矢量场分别为 ![]() 和
和 ![]() . 然后在曲面
. 然后在曲面 ![]() 使用
使用 ![]() ,其中选择
,其中选择 ![]() ,使得
,使得 ![]() 垂直于梯度
垂直于梯度 ![]() ,尤其是
,尤其是 ![]() . 在图两边显示的点之外,
. 在图两边显示的点之外,![]() 和
和 ![]() 都具有同样的符号. 在左边
都具有同样的符号. 在左边 ![]() ,因为
,因为 ![]() 和
和 ![]() ,在右边
,在右边 ![]() ,因为
,因为 ![]() 和
和 ![]() ,在这两种情况下,迹退出滑动模式. 这些点可以通过数值查找合适的根
,在这两种情况下,迹退出滑动模式. 这些点可以通过数值查找合适的根 ![]() 或
或 ![]() 找到.
找到.
考虑矢量场 ![]() . 一旦
. 一旦 ![]() ,矢量场又开始指向下,迹可以逃离滑动模式.
,矢量场又开始指向下,迹可以逃离滑动模式.
考虑矢量场 ![]() . 对于
. 对于 ![]() ,这只是一个具有负阻尼的振荡器. 对于
,这只是一个具有负阻尼的振荡器. 对于 ![]() ,所有迹趋近于不连续曲面
,所有迹趋近于不连续曲面 ![]() . 在
. 在 ![]() ,如果
,如果 ![]() 不是太大,有一组点,其中有滑动运动. 滑动运动有效地稳定带有负阻尼会产生的无界生长,因此那是一个周期性轨道.
不是太大,有一组点,其中有滑动运动. 滑动运动有效地稳定带有负阻尼会产生的无界生长,因此那是一个周期性轨道.
目前为止示范的所有范例都是二维的,因为它很容易可视化. 然而,连续性适用于任何维数,当滑动于一个以上的不连续曲面,可以立即获得解.
考虑三维中两个非连续曲面,由球曲面 ![]() 和平面
和平面 ![]() 定义,并且矢量场为
定义,并且矢量场为 ![]() .
.
解首先沿着球曲面滑动,然后沿着两个曲面,最后只沿着平面滑动.
非连续符号差
对于带有复杂定义的函数,例如非连续性的符号处理是不可能的,有可能手动设置类似 NDSolve 自动处理非连续函数的非连续性处理.
非连续符号差变量是通过包括一个 WhenEvent 表达式来设置,其中事件是在非连续曲面,行为是规则设置变量给 "DiscontinuitySignature",并用 DiscreteVariables 选项指明变量的范围为 {-1,0,1} 或 {-1,1}.
| WhenEvent[e0,s[t]->"DiscontinuitySignature] | 指明离散变量 s[t] 保持由 e 定义的非连续曲面的非连续符号差,使得 s[t] 是有效的 Sign[e] |
| DiscreteVariables->{s[t]∈{-1,0,1}} | 表明 s[t] 是一个离散变量,具有可能的值为 -1、0 和 1;会考虑滑动模式解 |
| DiscreteVariables->{s[t]∈{-1,1}} | 表明 s[t] 是一个离散变量,具有可能的值为 -1 和 1,不会考虑滑动模式解 |
当遇到非连续性时,变量 ![]() 从
从 ![]() 切换到 0,解进入滑动模式. 滑动模式由0的非连续符号差表明,因为理想情况下,解是完全在非连续曲面
切换到 0,解进入滑动模式. 滑动模式由0的非连续符号差表明,因为理想情况下,解是完全在非连续曲面 ![]() ,因此
,因此 ![]() 为 0. 实践中,由于数值误差,实际解可能无法满足. 当在滑动模式中,NDSolve 试着尽可能地靠近曲面.
为 0. 实践中,由于数值误差,实际解可能无法满足. 当在滑动模式中,NDSolve 试着尽可能地靠近曲面.
如果你知道非连续性不会导致滑动模式,如果你把0从非连续符号差变量中排除,所需要的计算可能成本更低. 然而,如果你这样做,可能在非连续性上有滑动模式,解会失败或不正确.
定义,可以由 ![]() 表示,其中
表示,其中 ![]() 由 NDSolve 中 Wolfram 语言表达式 WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"] 设定.
由 NDSolve 中 Wolfram 语言表达式 WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"] 设定.
事件函数的时间导数,![]() 在决定当在某段时间
在决定当在某段时间 ![]() ,
, ![]() 时发生什么是很重要的. 有六中情况,其中
时发生什么是很重要的. 有六中情况,其中 ![]() 会改变,且
会改变,且 ![]() ,WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"].
,WhenEvent[e[x[t]]>0,s[t]->"DiscontinuitySignature"].
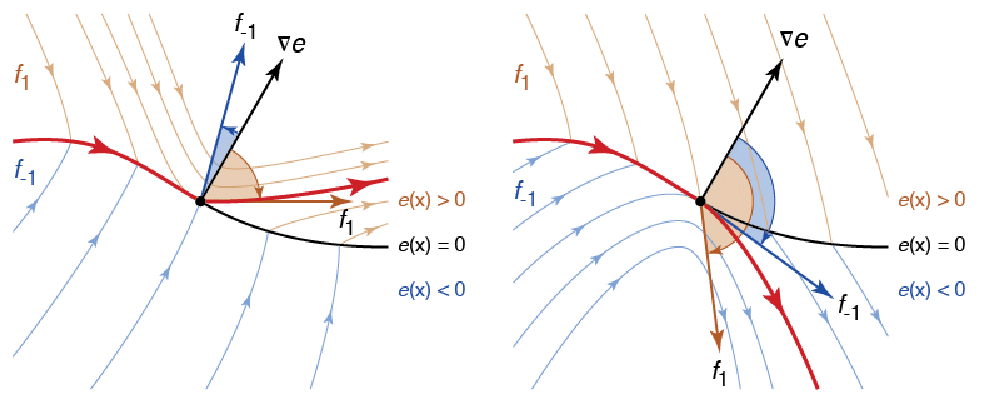
- 情况 3:(从上面进入滑动模式)对于
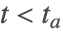 ,且在
,且在  ,
,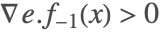 ,有
,有  且
且  . 因为
. 因为 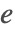 减少至0且在
减少至0且在  时保持
时保持  . 导数
. 导数 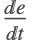 是在负上和正下不连续性,因此迹被限制在不连续处. 这被称为滑动模式,
是在负上和正下不连续性,因此迹被限制在不连续处. 这被称为滑动模式, 的值被设为 0. 有效的矢量场
的值被设为 0. 有效的矢量场 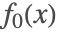 是使用 Filippov 连续性
是使用 Filippov 连续性  计算,其中
计算,其中 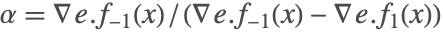 . 注意
. 注意 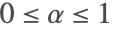 ,因为
,因为 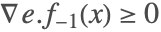 且
且 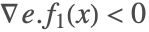 .
.
范例
自由落体
该系统对在遇到空气阻力的情况下、由于引力作用的自由落体进行建模(见 [M04]).
范德波尔振荡器的周期
范德波尔振荡器是常微分方程的一个极端刚性系统的例子. 事件定位方法可以调用任何方法来对常微分方程系统进行实际积分. 默认方法,Automatic,在必要时会自动切换至适用于刚性系统的方法,使得刚性不至引出什么问题.
通过选择 NDSolve 解的端点,就可以编写一个函数,以返回作为 ![]() 的一个函数的周期.
的一个函数的周期.
庞加莱截面
对于一个交互式图形界面,参阅程序包 EquationTrekker.
Hénon–Heiles系统
定义 Hénon–Heiles 系统,该系统对星系中的恒星运动进行建模.
在这种情况下,我们感兴趣的庞加莱截面是当轨道通过 ![]() 时
时 ![]() 平面中点的集合.
平面中点的集合.
由于数值积分的实际结果并不是必须的,有可能可以通过把输出变量列表(NDSolve 的第二个变量中)指定为空,或者 {} 来避免把所有数据存储在 InterpolatingFunction 中. 这意味着 NDSolve 不会产生InterpolatingFunction 作为输出,避免了存储大量不必要的数据. NDSolve 的确发出一条消息 NDSolve::noout 警告将不会有输出函数,但是在这种情况下,它可以安全地被关闭,因为我们所感兴趣的数据是从事件动作中收集到的.
这里使用了线性插值事件定位方法,因为这里计算的目的是在分辨率相对较低的图像中查看结果. 如果用户正在做一个需要放大图像以查看详细信息或者找到某个特征的例子,比如庞加莱 map 中的一个固定点,那么使用默认的定位方法就更加适合了.
由于 Hénon–Heiles 系统是哈密顿的,一个辛方法提供了这个例子的更好的定性结果.
ABC 流
弹跳球
这个例子是 [SGT03] 中一个例子的推广. 它对一个沿着具有给定形状的坡道弹跳的球进行建模. 这个例子很好地演示了用户可以如何使用具有事件定位的 NDSolve 的多次调用来对某些行为进行建模.
避免偏微分方程中的 Wraparound
许多演化方程对这样一个空间域内的行为建模,该空间域是无限的或者足够大以至于无法不使用专门的离散方法对整个域进行离散化. 在实践中,通常的情况是,只要我们感兴趣的解依然是局域化的,我们就有可能一直使用较小的计算域.
当计算域的边界由实际考虑制定,而不是根据研究的实际模型制定时,我们就可能适当地选择边界条件. 因为周期性拟谱逼近的良好的分辨率,使用具有周期性边界条件的 "Pseudospectral Derivatives" 方法可以增加计算域的范围. 周期性边界条件的缺点是传播过边界的信号在域的另一边继续,从而通过 wraparound 影响了解. 我们有可能在接近边界处使用一个吸收层以最小化这些效果,但是并不总是可能完全消除它们.
Sine-Gordon 方程出现在微分几何和相对场论中. 这个例子从一个局部化的初始条件开始,对方程进行积分.周期性的拟谱方法用于积分. 由于没有在边界附近设置吸收层,最适当的办法是,一旦 wraparound 变得显著,即停止积分. 这种条件很容易通过使用 WhenEvent,用事件定位检测到.
三体问题
这个例子说明受限的三体问题(由四个方程组成的标准非刚性测试系统)的解. 这个例子追踪了绕着月球旅行、并且返回地球的飞船的路径(见 [SG75]的第 246 页). 指明多个事件和零点交叉方向的能力是重要的.
前两个解的组成部分是无穷小质量的物体的坐标,所以画出一个对另一个的图形就能给出物体的轨道.
具有延迟的传染模型
非连续符号差和 C 代码
对于符号式指定的微分方程组,NDSolve 会自动扫描方程组查找非连续函数,并设置事件以便正确处理非连续性. 如果一个微分系统是通过计算一个不可能进行符号式扫描的函数来定义的话,那么有必要设置非连续符号差变量和事件来处理可能内嵌于定义的非连续性.
用 C 代码定义并编译与 LibraryFunction Wolfram 语言相链接的函数是 Wolfram 语言不能进行符号式扫描的一个很好的范例.