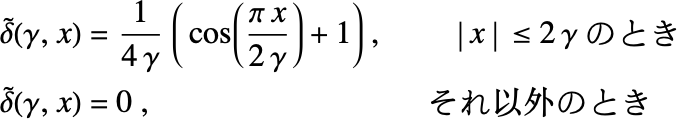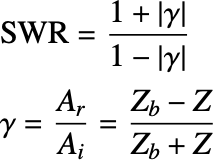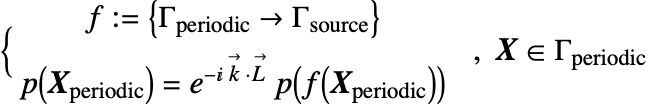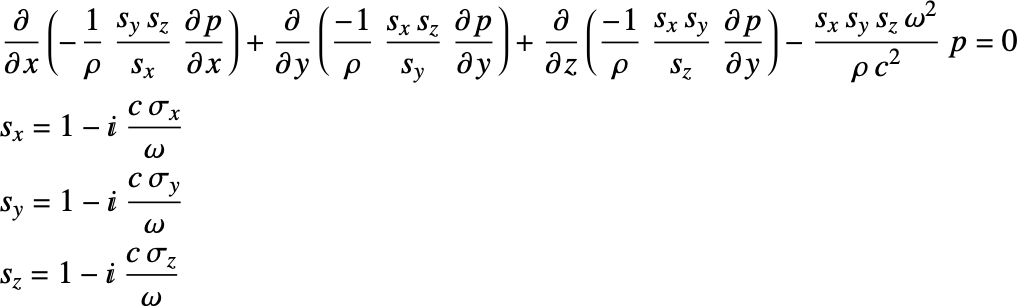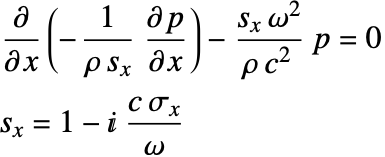Acoustics in the Frequency Domain
| Contents | Perfectly Matched Layer |
| Introduction | Nomenclature |
| Helmholtz Equation | References |
| Acoustic Boundary Conditions |
Contents
Introduction
Acoustics is the field of physics that models sound waves by changes in pressure. Two approaches to modeling acoustic systems are common: one approach is to model acoustics in the time domain and the other is to model in the frequency domain. This tutorial focuses on the modeling of sound in the frequency domain and makes use of the Helmholtz partial differential equation (PDE) as the model. The acoustic modeling in the frequency domain introduced here will build on concepts introduced in the tutorial Acoustics in the Time Domain, which should be read as a first exposure to acoustics modeling. Since the two approaches are related, the relations will be presented throughout this tutorial.
The main model of acoustics in the frequency domain is the Helmholtz equation. The Helmholtz PDE is a time-independent equation. Because the Helmholtz PDE is a time-independent PDE, it can be solved more efficiently compared to the time-dependent wave equation used for modeling acoustics in the time domain. The Helmholtz equation is, however, only applicable when modeling acoustic systems that have a harmonic time dependency. In other words, inharmonic sound signals have to be modeled in the time domain, and the benefits of using the Helmholtz equation cannot be exploited.
Two types of analysis in the frequency domain are introduced in this tutorial: Time-Harmonic Analysis and Eigenfrequency Analysis. Both the time-harmonic and the eigenfrequency analysis are based on the Helmholtz PDE model in conjunction with various types of boundary conditions, which are also introduced in this tutorial. The purpose of a time-harmonic analysis is to compute the frequency response of an acoustic system over a range of frequencies. An eigenfrequency analysis, on the other hand, is applied to solve for the eigenmodes and eigenfrequencies of an acoustic system. The actual analysis of a time-harmonic model is done with ParametricNDSolve, and for an eigenfrequency analysis, NDEigensystem is made use of.
Extended examples of sound system modeling can be found in the Model Collection.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Time-Harmonic Analysis
Time-harmonic analysis is a branch of acoustics concerned with the frequency response of an acoustic system. A sound signal is referred to as time harmonic if it can be expressed as a sine function with a specific frequency. For a time-harmonic analysis, an acoustic system is exposed to several harmonic sound signals over a range of frequencies, and the performance of the device at the frequency of interest is analyzed. This type of analysis is important when building frequency-dependent acoustic systems, for example, a lowpass filter that is designed to attenuate sound at higher frequencies.
In response to harmonic stimulus, the resulting sound pressure field ![]() can be shown to be time harmonic as well [1]. A sound pressure field is said to be time harmonic if the pressure variation at any spatial position
can be shown to be time harmonic as well [1]. A sound pressure field is said to be time harmonic if the pressure variation at any spatial position ![]() has a sinusoidal time dependence with an angular frequency
has a sinusoidal time dependence with an angular frequency ![]() .
.
A general expression of a harmonic sound pressure field ![]() is written as:
is written as:
Here, ![]() denotes the amplitude at the given position, and
denotes the amplitude at the given position, and ![]() is an initial phase shift at
is an initial phase shift at ![]() . In cases where two sound signals have no phase difference
. In cases where two sound signals have no phase difference ![]() , they are said to be "in phase". If the phase difference happens to be
, they are said to be "in phase". If the phase difference happens to be ![]()
![]() , the two sound signals are said to be "in antiphase".
, the two sound signals are said to be "in antiphase".
For analytical convenience, the time-harmonic relation (2) is often expressed in complex form known as the complex exponential representation (CER):
By convention, the CER expression is often expressed simply as:
in which it is implicitly interpreted that the real part of the complex expression represents the real function ![]() .
.
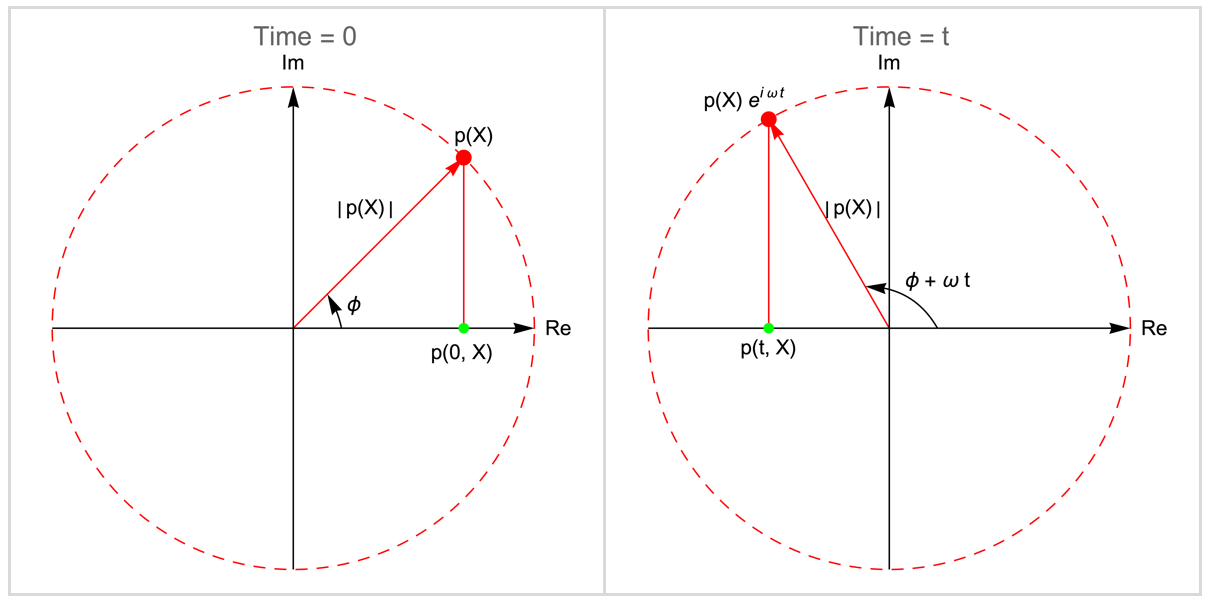
The CER expression can be understood as a rotating vector ![]() in the complex plane. The following figure illustrates this behavior.
in the complex plane. The following figure illustrates this behavior.
The rotating vector ![]() is known as the complex amplitude function. The amplitude function
is known as the complex amplitude function. The amplitude function ![]() rotates counterclockwise at a speed of the angular frequency
rotates counterclockwise at a speed of the angular frequency ![]() . At any given time
. At any given time ![]() , the projection of
, the projection of ![]() on the real axis represents the transient sound pressure
on the real axis represents the transient sound pressure ![]() , and the vector length
, and the vector length ![]() corresponds to the local amplitude.
corresponds to the local amplitude.
If the amplitude function and its complex conjugate are expressed as ![]() and
and ![]() , then the local amplitude
, then the local amplitude ![]() can be calculated by:
can be calculated by:
When the time-harmonic relation (3) is inserted into the wave equation, the equation simplifies to a time-independent Helmholtz equation. The derivation of the Helmholtz equation from a wave equation will be presented in a later section entitled Derivation of the Frequency Acoustics Model from Time Domain Model. For now, it is important to understand that an unknown sound field can be solved for in the frequency domain by using the angular frequency ![]() in the Helmholtz PDE model (4):
in the Helmholtz PDE model (4):
The terms ![]() and
and ![]() are monopole and dipole sources, respectively.
are monopole and dipole sources, respectively.
The computed solution ![]() , however, can be easily transformed back into the time domain using the time-harmonic relation (5).
, however, can be easily transformed back into the time domain using the time-harmonic relation (5).
Eigenfrequency Analysis
If the monopole source ![]() and the dipole source
and the dipole source ![]() are removed from the Helmholtz PDE model (6), the equation simplifies to the source-free Helmholtz equation:
are removed from the Helmholtz PDE model (6), the equation simplifies to the source-free Helmholtz equation:
Equation (7) can be treated as an eigenvalue problem such that ![]() , and can be solved with NDEigensystem. Here, the differential operator
, and can be solved with NDEigensystem. Here, the differential operator ![]() corresponds to the left-hand side of (8), and
corresponds to the left-hand side of (8), and ![]() represents the eigenvalue of the eigensystem.
represents the eigenvalue of the eigensystem.
The set of eigenvalues ![]() that fulfills the source-free Helmholtz equation gives the corresponding eigenfrequencies
that fulfills the source-free Helmholtz equation gives the corresponding eigenfrequencies ![]() by:
by:
The amplitude function ![]() that is paired with each eigenvalue
that is paired with each eigenvalue ![]() is called eigenmode.
is called eigenmode.
The eigenfrequency ![]() is also known as the natural frequency, which determines the resonance of an acoustic system. To illustrate the acoustic resonance, consider an open-ended tube and a closed-ended tube. Both tubes are filled with air, and the length
is also known as the natural frequency, which determines the resonance of an acoustic system. To illustrate the acoustic resonance, consider an open-ended tube and a closed-ended tube. Both tubes are filled with air, and the length ![]() .
.
By convention, the closed-ended tube denotes a tube with one closed end only.
Since the medium pressure must be equal to the ambient reference pressure at the open end, the sound pressure is fixed at zero such that ![]() . At the closed end, however, the sound pressure accumulates and reaches its maximum value, since no forward motion is possible. Due to these boundary conditions, the tube can only sustain sound waves at certain frequencies, that is, the eigenfrequencies.
. At the closed end, however, the sound pressure accumulates and reaches its maximum value, since no forward motion is possible. Due to these boundary conditions, the tube can only sustain sound waves at certain frequencies, that is, the eigenfrequencies.
At each eigenfrequency ![]() , a standing wave forms within the tube. The lowest eigenfrequency, which corresponds to eigenmode 1, is called the fundamental frequency. As shown in the acoustics time domain tutorial, compared to a traveling wave with the same amplitude, a standing wave needs a weaker sound source. In other words, a sound source excites an acoustic system the most at each eigenfrequency.
, a standing wave forms within the tube. The lowest eigenfrequency, which corresponds to eigenmode 1, is called the fundamental frequency. As shown in the acoustics time domain tutorial, compared to a traveling wave with the same amplitude, a standing wave needs a weaker sound source. In other words, a sound source excites an acoustic system the most at each eigenfrequency.
Eigenfrequency analysis is therefore an important consideration when designing acoustic systems that utilize (or prevent) resonance, such as musical instruments, acoustic filters and concert halls.
Helmholtz Equation
Introduction to Helmholtz Equation
The behavior of an acoustics system in the frequency domain is investigated by repetitively solving the Helmholtz PDE for a specific frequency out of a frequency range of interest. The Helmholtz equation (9) is used for modeling a harmonic sound pressure field at a specific angular frequency ![]() :
:
The dependent variable in the Helmholtz equation is the sound pressure ![]() . The sound pressure wave is propagating in a medium with density
. The sound pressure wave is propagating in a medium with density ![]() at the speed of sound
at the speed of sound ![]() . The sound pressure field is modeled in response to a harmonic sound stimulus at a frequency
. The sound pressure field is modeled in response to a harmonic sound stimulus at a frequency ![]() , which is related to the angular frequency
, which is related to the angular frequency ![]() by
by ![]() .
.
Sound pressure can be understood as the local pressure deviation from an ambient reference pressure: ![]() , where
, where ![]() denotes the position vector. Terms
denotes the position vector. Terms ![]() and
and ![]() represent monopole and dipole sources, respectively. The Source Types section describes these sound sources.
represent monopole and dipole sources, respectively. The Source Types section describes these sound sources.
Various sections in the documentation explain the use of inactive PDE operators. Please refer to Numerical Solution of Partial Differential Equations.
As shown in the tutorial Acoustics in the Time Domain, the transient acoustic model can be set up in a similar way.
Note that for the frequency domain acoustic model, the time-derivative term ![]() has been converted to the frequency-dependent term
has been converted to the frequency-dependent term ![]() by using the time-harmonic relation (10). The derivation can be found in the following section: Derivation of the Drequency Acoustics Model from Time Domain Model.
by using the time-harmonic relation (10). The derivation can be found in the following section: Derivation of the Drequency Acoustics Model from Time Domain Model.
The following model parameters are used for the examples in this tutorial. These parameters define the simulation domain ![]() .
.
The following 1D example shows a frequency domain acoustic model simulation. In the first step, a time-harmonic analysis will be performed, and in the subsequent step, an eigensystem analysis is done of the same acoustic mode. The relation between the two analysis types will then be apparent.
In a next step, an eigenvalue analysis is performed.
Note that at each eigenfrequency ![]() , the amplitude response
, the amplitude response ![]() reaches its local maximum.
reaches its local maximum.
Derivation of the Frequency Acoustics Model from the Time Domain Model
The Helmholtz equation is derived from the wave equation (11) with harmonic time dependence. The general wave equation is given as:
Here the terms ![]() and
and ![]() are monopole and dipole sources, respectively.
are monopole and dipole sources, respectively.
Recall that if a sound pressure field is assumed to be time harmonic, the pressure variation in time for a particular frequency ![]() can be expressed in the complex plane by an amplitude function
can be expressed in the complex plane by an amplitude function ![]() :
:
Likewise, the monopole and dipole sources can be expressed by amplitude functions ![]() and
and ![]() , respectively:
, respectively:
Taking the second-order time derivative of (12) gives:
Taking the gradient of (13) yields:
Inserting (14), (15), (16) into (17), the wave equation becomes:
Factor out the common term ![]() ; then the equation simplifies to the time-independent, inhomogeneous Helmholtz equation (18):
; then the equation simplifies to the time-independent, inhomogeneous Helmholtz equation (18):
Model Parameter Setup
In acoustics simulations, the wavelength ![]() of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution of the governing partial differential equation. Here, a function is created to set the MaxCellMeasure for time-harmonic waves.
of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution of the governing partial differential equation. Here, a function is created to set the MaxCellMeasure for time-harmonic waves.
For a time-harmonic wave, the wavelength is ![]() . The default resolution of the max edge length is set to 12 nodes per
. The default resolution of the max edge length is set to 12 nodes per ![]() , which means that there will be at least 12 elements per wavelength
, which means that there will be at least 12 elements per wavelength ![]() in each direction of the wave propagation. Typically, this is sufficient to resolve waves accurately [19]. However, it is always possible to assign other resolution values to meet different accuracy requirements.
in each direction of the wave propagation. Typically, this is sufficient to resolve waves accurately [19]. However, it is always possible to assign other resolution values to meet different accuracy requirements.
Many examples will be using a radiation boundary condition to produce a harmonic sound wave and an absorbing boundary condition to avoid wave reflection.
Source Types
The Helmholtz PDE model (20) contains two types of time-harmonic sources: monopole ![]() and dipole sources
and dipole sources ![]() . The following sections will demonstrate how these sound sources are set up for modeling in the frequency domain. The physical meaning of sound sources is explained in detail in the acoustics time domain tutorial.
. The following sections will demonstrate how these sound sources are set up for modeling in the frequency domain. The physical meaning of sound sources is explained in detail in the acoustics time domain tutorial.
Monopole Sources
The monopole source ![]() from the Helmholtz equation (21) models a point source that radiates sound isotropically. An example of an acoustic monopole would be a small sphere whose radius alternately expands and contracts [22].
from the Helmholtz equation (21) models a point source that radiates sound isotropically. An example of an acoustic monopole would be a small sphere whose radius alternately expands and contracts [22].
To make use of a monopole source, the monopole source strength ![]() and the source location
and the source location ![]() need to be specified. The monopole source term
need to be specified. The monopole source term ![]() may be written as:
may be written as:
where ![]() is a regularized Dirac delta function at the source location.
is a regularized Dirac delta function at the source location.
There are various techniques to regularize the delta function [23,24], such as:
where ![]() is the regularization parameter that controls the support of the regularized delta functions
is the regularization parameter that controls the support of the regularized delta functions ![]() . Typically,
. Typically, ![]() should have a size comparable to the mesh spacing
should have a size comparable to the mesh spacing ![]() .
.
As shown in the section entitled Time-Harmonic Analysis, the solution from the Helmholtz PDE is the complex-valued amplitude function ![]() , which contains the information of both phase and amplitude. The amplitude of the sound pressure corresponds to the absolute value or complex modulus
, which contains the information of both phase and amplitude. The amplitude of the sound pressure corresponds to the absolute value or complex modulus ![]() .
.
In a 1D domain, the sound pressure amplitude ![]() is constant for the monopole source
is constant for the monopole source ![]() at each particular frequency. Within the source region
at each particular frequency. Within the source region ![]() , there is a small deviation in
, there is a small deviation in ![]() due to the discrete nature of the regularized delta function
due to the discrete nature of the regularized delta function ![]() used. A finer mesh can be used to reduce the numerical error.
used. A finer mesh can be used to reduce the numerical error.
Note that for a given monopole source strength ![]() , the pressure amplitude reduces with higher frequencies. The analytical solution [25] for the amplitude in one dimension is given by:
, the pressure amplitude reduces with higher frequencies. The analytical solution [25] for the amplitude in one dimension is given by:
It is more intuitive to consider the sound pressure ![]() as a function of time. To do so, the amplitude function
as a function of time. To do so, the amplitude function ![]() should be transformed via the harmonic wave relation (26):
should be transformed via the harmonic wave relation (26): ![]() .
.
The monopole source is a point source that radiates sound isotropically at ![]() . The blue line here is the transient sound pressure
. The blue line here is the transient sound pressure ![]() , and the gray line is the analytical pressure amplitude inserted for a visual verification.
, and the gray line is the analytical pressure amplitude inserted for a visual verification.
As a comparison, a 2D monopole source is constructed in a similar manner.
For 2D and 3D monopoles, as the radiated sound wave spreads out from the source, a wider wavefront will be formed. Therefore, with a given monopole strength ![]() , the pressure amplitude
, the pressure amplitude ![]() will decrease with the distance to the source location.
will decrease with the distance to the source location.
Dipole Sources
A dipole source ![]() consists of two monopole sources of equal strength but opposite phase and separated by a distance
consists of two monopole sources of equal strength but opposite phase and separated by a distance ![]() . The separation distance is small compared to the wavelength of sound
. The separation distance is small compared to the wavelength of sound ![]() . An example of an acoustic dipole would be a small rigid sphere that oscillates sinusoidally [27]. Unlike a single monopole source
. An example of an acoustic dipole would be a small rigid sphere that oscillates sinusoidally [27]. Unlike a single monopole source ![]() , a dipole source does not radiate sound isotropically.
, a dipole source does not radiate sound isotropically.
In the acoustics time domain tutorial, it has been shown that a dipole source ![]() could be modeled by two identical monopole sources
could be modeled by two identical monopole sources ![]() . Here that intermediate step is not made, and modeling is done with a dipole source with the source term
. Here that intermediate step is not made, and modeling is done with a dipole source with the source term ![]() .
.
To make use of a dipole source, the dipole source strength ![]() and the source location
and the source location ![]() need to be specified. The dipole source term
need to be specified. The dipole source term ![]() may be written as:
may be written as:
where ![]() is the regularized delta function at the source location.
is the regularized delta function at the source location.
As shown in the section entitled Time-Harmonic Analysis, the solution from the Helmholtz PDE is the complex-valued amplitude function ![]() , which contains the information of both phase and amplitude. The amplitude of the sound pressure corresponds to the absolute value or complex modulus
, which contains the information of both phase and amplitude. The amplitude of the sound pressure corresponds to the absolute value or complex modulus ![]() .
.
In the 1D domain, the sound pressure amplitude ![]() is constant outside each dipole source region. Since the embedded monopole sources are in opposite phase, the amplitude at the source location
is constant outside each dipole source region. Since the embedded monopole sources are in opposite phase, the amplitude at the source location ![]() sums to zero. The analytical solution [28] for the pressure amplitude in 1D is given by:
sums to zero. The analytical solution [28] for the pressure amplitude in 1D is given by:
The numerical solution plot above, however, is slightly different from the analytical solution, due to the discrete nature of the regularized delta function ![]() used. A finer mesh can be used to reduce the numerical error.
used. A finer mesh can be used to reduce the numerical error.
It is more intuitive to consider the sound pressure ![]() as a function of time. To do so, the amplitude function
as a function of time. To do so, the amplitude function ![]() should be transformed via the harmonic wave relation (29):
should be transformed via the harmonic wave relation (29): ![]() .
.
The dipole source does not radiate sound isotropically. The resultant sound waves are sinusoidal but in opposite phase.
As a comparison, a 2D dipole source is constructed in a similar manner.
For 2D and 3D dipoles, the radiated sound wave does not spread out equally in all directions [30]. Therefore, with a given dipole strength ![]() , the pressure amplitude
, the pressure amplitude ![]() will depend on both the spatial direction and the distance to the source location.
will depend on both the spatial direction and the distance to the source location.
Sound Propagation in Lossy Media
As shown in the acoustics time domain tutorial, it is possible to model sound propagation in lossy media with a given porosity ![]() , flow resistivity
, flow resistivity ![]() and an effective bulk modulus
and an effective bulk modulus ![]() . The modified wave equation is:
. The modified wave equation is:
Inserting the harmonic wave relation ![]() and factoring out the common term
and factoring out the common term ![]() , the equation (31) becomes:
, the equation (31) becomes:
Equation (32) is the modified Helmholtz equation that is used to model sound attenuation in the frequency domain.
The effective bulk modulus ![]() is frequency dependent [33] and can be approximated by an empirical formula:
is frequency dependent [33] and can be approximated by an empirical formula:
To illustrate the lossy media model, a sound wave propagating through a tube filled with a porous absorber is considered. The porosity and flow resistivity of this material are given by ![]() and
and ![]() , respectively.
, respectively.
An absorbing boundary condition is added on the right to avoid a reflection of the wave. Note that the NeumannValue is set to ![]() [34] to accommodate for the modified Helmholtz equation (35).
[34] to accommodate for the modified Helmholtz equation (35).
Since the effective bulk modulus ![]() in (36) is a frequency-dependent variable, the attenuation rate of the amplitude
in (36) is a frequency-dependent variable, the attenuation rate of the amplitude ![]() also varies with different frequencies. The small wiggles near the right end result from the numerical reflection on the absorbing boundary and can be reduced by using a finer mesh.
also varies with different frequencies. The small wiggles near the right end result from the numerical reflection on the absorbing boundary and can be reduced by using a finer mesh.
The amplitude of the sound pressure wave decays as it propagates to the right. Note that the attenuation rate slightly varies with different frequencies.
A Comparison of Time-Domain and Frequency-Domain Modeling
An acoustic system can be modeled both in the time domain and the frequency domain. As shown in the acoustics time domain tutorial, the wave equation is used to find a transient solution of a sound wave in the time domain. Whenever the excitation of a sound pressure field is time harmonic, the Helmholtz equation can be used to directly solve for a steady-state solution of a sound pressure field in the frequency domain. Each approach has its own strength and constraints and is summarized in the following table.
| Time-Domain Modeling | Frequency-Domain Modeling | |
| Governing PDE | Wave equation | Helmholtz equation |
| Dependent variable | transient p(t,X) | stationary p(X) |
| Harmonic excitation | yes | yes |
| Inharmonic excitation | yes | no |
| Computational cost | high | low |
| Accuracy | low | high |
In other words, if an acoustic system has a time-inharmonic dependency, then it needs to be modeled in the time domain, and the benefits of using the Helmholtz equation cannot be exploited. But in all other cases, making use of the model in the frequency domain is beneficial.
To illustrate this behavior, an acoustic system of a right-traveling wave is considered in the next example. The simulation is done once in the time domain and once in the frequency domain. In both models, the simulation domain is set as four times of the wavelength ![]() , and the frequency is arbitrarily chosen at
, and the frequency is arbitrarily chosen at ![]() .
.
In the following example, a radiation boundary condition is added on the left to produce a harmonic sound wave, and an absorbing boundary condition is placed on the right to avoid wave reflection.
First, the model is analyzed in the time domain, and following that, a frequency domain analysis will be performed. The results will be compared to each other.
Wave Equation: Time-Domain Modeling
For the wave equation model, the simulation end time ![]() is defined as the time required for the sound pressure field to reach its dynamic steady state.
is defined as the time required for the sound pressure field to reach its dynamic steady state.
The result shows a transient sound pressure wave traveling to the right.
Next, the same model is built with the Helmholtz equation.
Helmholtz Equation: Frequency-Domain Modeling
Note that the setup of the equation does not change. All changes are done through changing the variables and parameters.
Since the Helmholtz equation directly computes a stationary solution of a sound pressure field, there is no need to do the time integration in the solving process. The computational cost is thus reduced significantly.
The result of the Helmholtz equation is a steady-state sound pressure field ![]() . To transform the solution into the time domain, the harmonic wave relation can be used:
. To transform the solution into the time domain, the harmonic wave relation can be used:
To transform a transient solution into the frequency domain, however, requires a Fourier analysis [37]. The process is to decompose the transient sound signal into a sum of harmonic signals. Each harmonic signal has a specific frequency and a relative magnitude, which allows the transient signal to be mapped into the frequency domain.
The computational cost for solving the Helmholtz equation is so much lower that it is possible to solve the Helmholtz PDE repetitively with different frequencies, which makes it suitable for frequency-domain modeling.
Next, the accuracy of the wave equation model and the Helmholtz equation model are compared.
Accuracy Comparison
Since the wave-equation model is a time-dependent PDE, while the Helmholtz-equation model is not, the former is subject to an extra error from the numerical time integration. The Helmholtz model is therefore more accurate than the wave-equation model.
Acoustic Boundary Conditions
In the acoustics time domain tutorial, details of common acoustic boundary conditions and how they can be modeled in the time domain have been shown. To avoid repetition, the following section only describes how to build these boundary conditions in the frequency domain. For readers who are interested in the derivation and the physical explanation, please refer to the acoustics time domain tutorial.
Most common boundary conditions in acoustics can be modeled with DirichletCondition, NeumannValue and PeriodicBoundaryCondition and can be categorized in the following four types:
Generally speaking, in solver algorithms, a NeumannValue[g-q p(X) ,X∈Γb] is used to specify the flux over the boundary ![]() such that
such that ![]() holds.
holds.
However, in acoustic models, the dipole sources ![]() can only be specified within the domain and will always equal zero on any part of the boundary; thus they lead to
can only be specified within the domain and will always equal zero on any part of the boundary; thus they lead to ![]() .
.
For each boundary condition, a statement will be made whether the particular boundary condition is applicable for Time Harmonic Analysis or Eigenfrequency Analysis or both in the following manner:
| analysis type | applicable | |
| Time Harmonic | Yes/No | |
| Eigenfrequency | Yes/No |
Impedance Boundary Conditions
Formulation
With a specified impedance ![]() on the boundary
on the boundary ![]() , the impedance boundary condition is given by:
, the impedance boundary condition is given by:
Derivation
When a sound wave transits to another medium or encounters a partially reflective boundary, for example, a porous surface, part of the sound wave will be reflected at the interface and part will be transmitted across the interface.
One property that is used to formulate the relation between the incident, reflected and transmitted wave is called the specific acoustic impedance. The specific acoustic impedance ![]() is the ratio of the sound pressure to the sound particle velocity as the wave moves through the medium, which is defined as:
is the ratio of the sound pressure to the sound particle velocity as the wave moves through the medium, which is defined as:
The acoustics time domain tutorial shows that the impedance boundary condition can be formulated with a given boundary impedance ![]() as:
as:
Inserting the harmonic wave relation ![]() and factoring out the common term
and factoring out the common term ![]() , then the impedance boundary condition can be applied in the frequency domain as:
, then the impedance boundary condition can be applied in the frequency domain as:
Here the wave number ![]() denotes the ratio of angular frequency to the speed of sound.
denotes the ratio of angular frequency to the speed of sound.
An impedance boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Impedance Boundary Conditions in Time-Harmonic Analysis
To illustrate the impedance boundary condition, a tube with a porous surface at the right end is considered in the next example. The porous surface is treated as an impedance boundary, since it is a partially reflective boundary.
It is more intuitive to inspect the sound wave in the time domain. Recall that the solution can be transformed back into the time domain with the harmonic wave relation (38): ![]() .
.
Since the impedance boundary models a partially reflective boundary, there is more energy moving to the right than there is being reflected, which makes the resulting wave appear to travel to the right. Note that the maximum and the minimum values of the pressure amplitude are fixed in space (dashed lines). This type of wave is called a partial standing wave.
The ratio between the maximum and the minimum amplitudes is known as the standing wave ratio (SWR):
The standing wave ratio (SWR) is shown to be independent of the frequency. For an unknown boundary, the SWR can be used to measure the impedance ![]() and the reflection coefficient
and the reflection coefficient ![]() , given the specific acoustic impedance,
, given the specific acoustic impedance, ![]() , of the domain:
, of the domain:
Here ![]() and
and ![]() are the amplitude of the reflected and the incident wave, respectively.
are the amplitude of the reflected and the incident wave, respectively.
Absorbing Boundary Conditions
Formulation
With a specific type of incident wave and the distance ![]() between the wave origin to the boundary
between the wave origin to the boundary ![]() , the absorbing boundary condition is given by:
, the absorbing boundary condition is given by:
Derivation
Typically, a simulation domain that extends to infinity is not a feasible option in a simulation. Absorbing boundary conditions are a methodology used to model infinite domains. An absorbing boundary condition (ABC) works by absorbing an incoming wave and thus makes the model behave as if it had infinite extent. ABC are not the only way to model simulation domains with infinite extent. Perfectly Matched Layers (PML) may be used as an alternative approach to an ABC.
The time domain tutorial shows that the absorbing boundary condition is given by:
and inserting the harmonic wave relation ![]() gives the absorbing boundary condition in the frequency domain:
gives the absorbing boundary condition in the frequency domain:
Note that for a plane wave ![]() , for a cylindrical wave
, for a cylindrical wave ![]() and for a spherical wave
and for a spherical wave ![]() are used.
are used.
An absorbing boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Absorbing Boundary Conditions in Time-Harmonic Analysis
As an example, an infinitely long tube with the computational domain set from ![]() to
to ![]() is shown. To model the continuation of the domain, a plane wave absorbing boundary condition is added at the right end.
is shown. To model the continuation of the domain, a plane wave absorbing boundary condition is added at the right end.
Since the resulting sound pressure field is simply a right-traveling harmonic wave, the pressure amplitude is fixed at ![]() throughout the domain for all frequencies.
throughout the domain for all frequencies.
The incoming wave is absorbed at the right-hand boundary as if the simulation domain had infinite extent.
Sound Hard Boundary Conditions—Walls
Formulation
For a wall boundary ![]() , the sound hard boundary condition is given by:
, the sound hard boundary condition is given by:
Derivation
On a sound hard boundary, the normal component of the sound particle velocity ![]() is zero, since no forward motion is possible:
is zero, since no forward motion is possible:
Substituting (39) into the momentum conservation equation ![]() and applying the harmonic wave relation (40)
and applying the harmonic wave relation (40) ![]() , then the sound hard boundary condition can be formulated in the frequency domain as:
, then the sound hard boundary condition can be formulated in the frequency domain as:
If no boundary condition is specified on any part of the boundary, then by default a Neumann zero boundary condition is implicitly used. This implies that a sound hard boundary is the default boundary condition used if no boundary condition is specified at a given boundary.
A sound hard boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | Yes |
Sound Hard Boundary Conditions in Time-Harmonic Analysis
As an example for a time-harmonic analysis, look at a tube with one end closed.
The shape of the amplitude field shows several minima and maxima points, which are known as "nodes" and "antinodes", respectively. In the time domain, nodes are positions where the standing wave has no displacement and antinodes are the positions with maximal displacement. In the frequency domain, the displacements manifest themselves as minima and maxima. Since no forward motion is possible on the sound hard boundary, the sound pressure ![]() is fixed at its maximum at the right end, which means it is one of the antinodes. The maximum value
is fixed at its maximum at the right end, which means it is one of the antinodes. The maximum value ![]() corresponds to the double of the amplitude set by the radiation boundary.
corresponds to the double of the amplitude set by the radiation boundary.
It is more intuitive to inspect the result in the time domain.
Note that the sound wave moves neither right nor left but simply oscillates in time. This type of wave is known as a standing wave, which is formed by the superposition of two waves traveling in opposite directions.
In this case, the right-traveling wave is produced by the radiation boundary, and the left-traveling wave is the reflected wave from the sound hard boundary. For readers who are interested in the way that traveling waves superimpose to give a standing wave, please refer to the acoustics time domain tutorial.
Sound Hard Boundary Conditions in Eigenfrequency Analysis
Unlike a time-harmonic analysis, an eigenfrequency analysis aims to find the eigenfrequencies ![]() and the corresponding eigenmodes (eigenfunctions) of an acoustic system. In the next example, consider a tube with both ends closed.
and the corresponding eigenmodes (eigenfunctions) of an acoustic system. In the next example, consider a tube with both ends closed.
Note that the first eigenfrequency is zero, corresponding to the solution without any sound. The first pair of eigenfrequency/eigenmode is therefore a trivial solution and is denoted as eigenmode 0.
As explained previously, the sound pressure is fixed at its maximum on the sound hard boundaries since no forward motion is possible.
Normal Velocity Boundary Conditions
Formulation
With a specified sound particle velocity ![]() on the boundary
on the boundary ![]() , the normal velocity boundary condition is given by:
, the normal velocity boundary condition is given by:
Derivation
When a nonzero, time-harmonic sound particle velocity is specified at a boundary, then this type of boundary is called a normal velocity boundary:
Substituting (41) into the momentum conservation equation ![]() and applying the harmonic wave relation (42)
and applying the harmonic wave relation (42) ![]() , then the normal velocity boundary condition can be formulated in the frequency domain as:
, then the normal velocity boundary condition can be formulated in the frequency domain as:
A normal velocity boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Normal Velocity Boundary Conditions in Time-Harmonic Analysis
In the following example, a harmonic vibration is introduced at the right-hand boundary and vibrates with a known velocity amplitude ![]() . The sound field can be calculated by using NeumannValue, as shown below.
. The sound field can be calculated by using NeumannValue, as shown below.
Since the resulting wave is simply a left-traveling harmonic wave, the amplitude distribution is fixed throughout the domain for all frequencies.
The normal velocity boundary generates a harmonic wave on the right end that propagates to the left.
As shown in the acoustics time domain tutorial, a normal velocity boundary could be replaced by a pressure source boundary when the specific acoustic impedance ![]() is known.
is known.
Sound Soft Boundary Conditions
Formulation
The sound soft boundary condition is given by:
Derivation
On a sound soft boundary, the medium pressure is set equal to an ambient reference pressure, which means that the sound pressure at the boundary is fixed at zero: ![]() :
:
A sound soft boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | Yes |
Sound Soft Boundary Conditions in Time-Harmonic Analysis
A tube with one end open is considered as an example for the time-harmonic analysis. The open-ended side is treated as a sound soft boundary, since there is no constraint to limit the sound wave movement.
With ![]() , the sound pressure is a minimum at
, the sound pressure is a minimum at ![]() , where a sound soft boundary is positioned, and is thus called a node. The maximum value of the sound pressure field corresponds to the double of the amplitude set by the radiation boundary.
, where a sound soft boundary is positioned, and is thus called a node. The maximum value of the sound pressure field corresponds to the double of the amplitude set by the radiation boundary.
Similar to the sound hard boundary, the resulting wave is a standing wave that is formed by the superposition of two waves traveling in opposite directions.
In this case, the right-traveling wave is produced by the radiation boundary and the left-traveling wave is the reflected wave from the sound soft boundary. For readers who are interested in the way that traveling waves superimpose to give a standing wave, please refer to the acoustics time domain tutorial.
Sound Soft Boundary Conditions in Eigenfrequency Analysis
A tube with both ends open is used to illustrate the behavior of sound soft boundaries in an eigenfrequency analysis.
As expected, the sound pressure on the sound soft boundaries is fixed at zero.
Pressure Source Boundary Conditions
Formulation
With a specified pressure amplitude ![]() on the boundary
on the boundary ![]() , the pressure source boundary condition is given by:
, the pressure source boundary condition is given by:
Derivation
A pressure source boundary condition is spoken of when a nonzero, time-harmonic sound pressure is specified at a boundary. Both DirichletCondition and NeumannValue can be used to specify a pressure source boundary condition:
A pressure source boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Pressure Source Boundary Conditions in Time-Harmonic Analysis
To formulate the Dirichlet condition of a pressure source boundary, equation (43) is rewritten with the harmonic wave relation (44) ![]() :
:
Here ![]() denotes the amplitude of the pressure source.
denotes the amplitude of the pressure source.
Since the resulting wave is simply a left-traveling harmonic wave, the amplitude distribution is fixed at ![]() throughout the domain.
throughout the domain.
Similar to the normal velocity boundary, the pressure source generates a harmonic wave on the right end that propagates to the left.
A pressure source can also be modeled with a NeumannValue. As shown in the acoustics time domain tutorial, the NeumannValue setting for a pressure source is given by:
Insert the harmonic wave relation (45) ![]() ; then the pressure source boundary condition can be formulated in the frequency domain as:
; then the pressure source boundary condition can be formulated in the frequency domain as:
The animation shows the same effect as the Dirichlet model. For readers who are interested in the tradeoff between the Neumann model and the Dirichlet model of a pressure source boundary, please refer to the corresponding section in the acoustics time domain tutorial.
Radiation Boundary Conditions
Formulation
With a specified incident sound pressure ![]() and a wave direction vector
and a wave direction vector ![]() on the boundary
on the boundary ![]() , the radiation boundary condition is given by:
, the radiation boundary condition is given by:
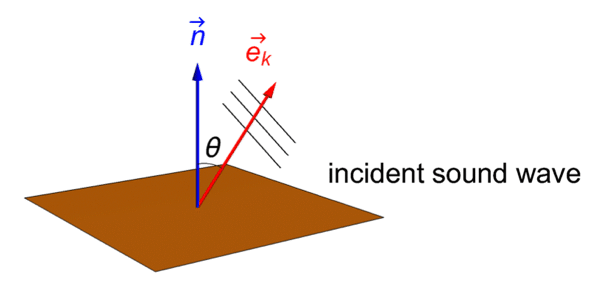
The relation among the boundary normal vector ![]() , the wave direction vector
, the wave direction vector ![]() and the wave incident angle
and the wave incident angle ![]() is illustrated below:
is illustrated below:
Therefore, equation (46) can also be expressed with a wave incident angle ![]() as:
as:
Note that when applying a radiation boundary in the 1D domain, the incident angle ![]() is always zero (i.e. normal incidence) and the equation (47) simplifies to:
is always zero (i.e. normal incidence) and the equation (47) simplifies to:
A 1D radiation boundary example will be shown in the following section. A 2D example, which demonstrated a radiated sound wave with oblique incidence, is presented here.
Derivation
A radiation boundary is a hybrid boundary condition that combines the properties of a pressure source boundary and an absorbing boundary. A time-harmonic sound pressure ![]() is specified at a boundary to produce an incoming wave; however, unlike a simple pressure source, the radiation boundary allows an outgoing wave to leave the computational domain with little reflection.
is specified at a boundary to produce an incoming wave; however, unlike a simple pressure source, the radiation boundary allows an outgoing wave to leave the computational domain with little reflection.
As shown in the acoustics time domain tutorial, the radiation boundary condition is given by:
Insert the harmonic wave relation (48) ![]() ; then the radiation boundary condition can be formulated in the frequency domain as:
; then the radiation boundary condition can be formulated in the frequency domain as:
A radiation boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Radiation Boundary Conditions in Time-Harmonic Analysis
As an example, a semi-infinite tube with one end closed is considered in the next example. The right end is treated as a radiation boundary where the harmonic sound wave enters the computational domain, and the closed left end is set as a sound hard boundary.
The resulting sound pressure field shows a standing wave, which is formed by the superposition of both incoming and outgoing waves. In this case, the radiation boundary at ![]() generates an incoming left-traveling wave, and the implicit sound hard boundary at
generates an incoming left-traveling wave, and the implicit sound hard boundary at ![]() reflects the wave to the right as an outgoing wave, which leaves the domain from the radiation boundary without constraint. For readers who are interested in the way that traveling waves superimpose to give a standing wave, please refer to the acoustics time domain tutorial.
reflects the wave to the right as an outgoing wave, which leaves the domain from the radiation boundary without constraint. For readers who are interested in the way that traveling waves superimpose to give a standing wave, please refer to the acoustics time domain tutorial.
Floquet Periodic Boundary Conditions
Formulation
Given a function ![]() that maps the sound pressure
that maps the sound pressure ![]() from the source boundary
from the source boundary ![]() to the periodic boundary
to the periodic boundary ![]() , the Floquet periodic boundary condition can be written as:
, the Floquet periodic boundary condition can be written as:
Here ![]() is the offset distance from the periodic boundary
is the offset distance from the periodic boundary ![]() to the source boundary
to the source boundary ![]() , and
, and ![]() is the wave number vector that denotes the direction of the sound wave.
is the wave number vector that denotes the direction of the sound wave.
Derivation
A Floquet periodic boundary condition is used to model a time-harmonic acoustic wave within a spatially periodic domain. That is, the information obtained from one boundary, referred to as the source boundary ![]() , can be mapped to another boundary, referred as the periodic boundary
, can be mapped to another boundary, referred as the periodic boundary ![]() , with a mapping function
, with a mapping function ![]() . The Floquet periodic boundary condition is set up with a PeriodicBoundaryCondition in the acoustic PDE model.
. The Floquet periodic boundary condition is set up with a PeriodicBoundaryCondition in the acoustic PDE model.
A Floquet periodic boundary condition can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Floquet Periodic Boundary Conditions in Time-Harmonic Analysis
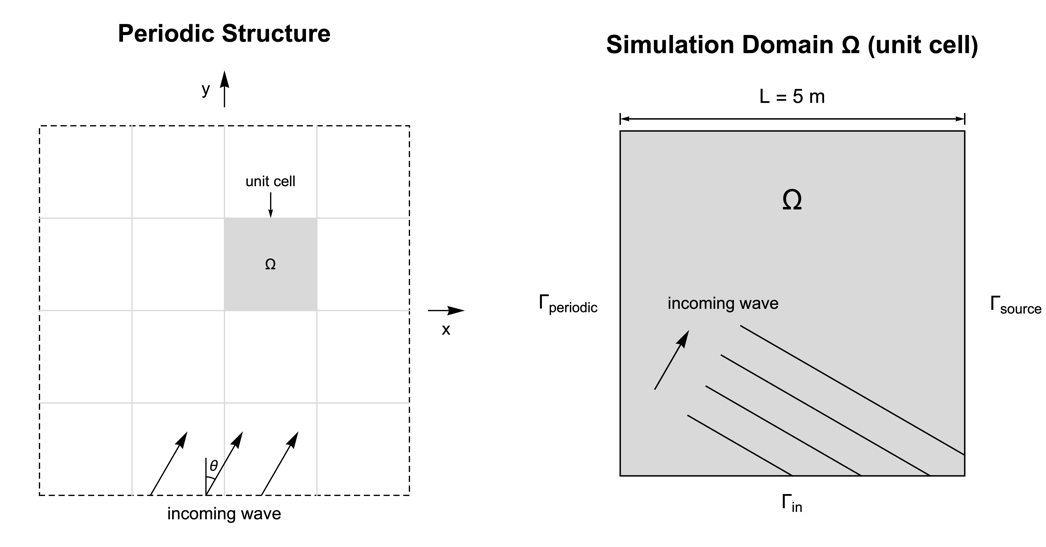
As an example, consider the following periodic structure in the ![]() plane. The structure is assumed to extend to infinity along the
plane. The structure is assumed to extend to infinity along the ![]() and
and ![]() directions. With the usage of the periodic boundary condition, it is possible to truncate the structure and take the unit cell as the simulation domain
directions. With the usage of the periodic boundary condition, it is possible to truncate the structure and take the unit cell as the simulation domain ![]() .
.
In this model, an acoustic wave is coming from the bottom edge with an incident angle ![]() and is modeled with a 2D radiation boundary denoted as
and is modeled with a 2D radiation boundary denoted as ![]() . The periodic boundary
. The periodic boundary ![]() is set on the left edge and the source boundary
is set on the left edge and the source boundary ![]() on the right edge, so that when the sound wave passes through the right side of the domain
on the right edge, so that when the sound wave passes through the right side of the domain ![]() , it reappears on the left side with the same magnitude.
, it reappears on the left side with the same magnitude.
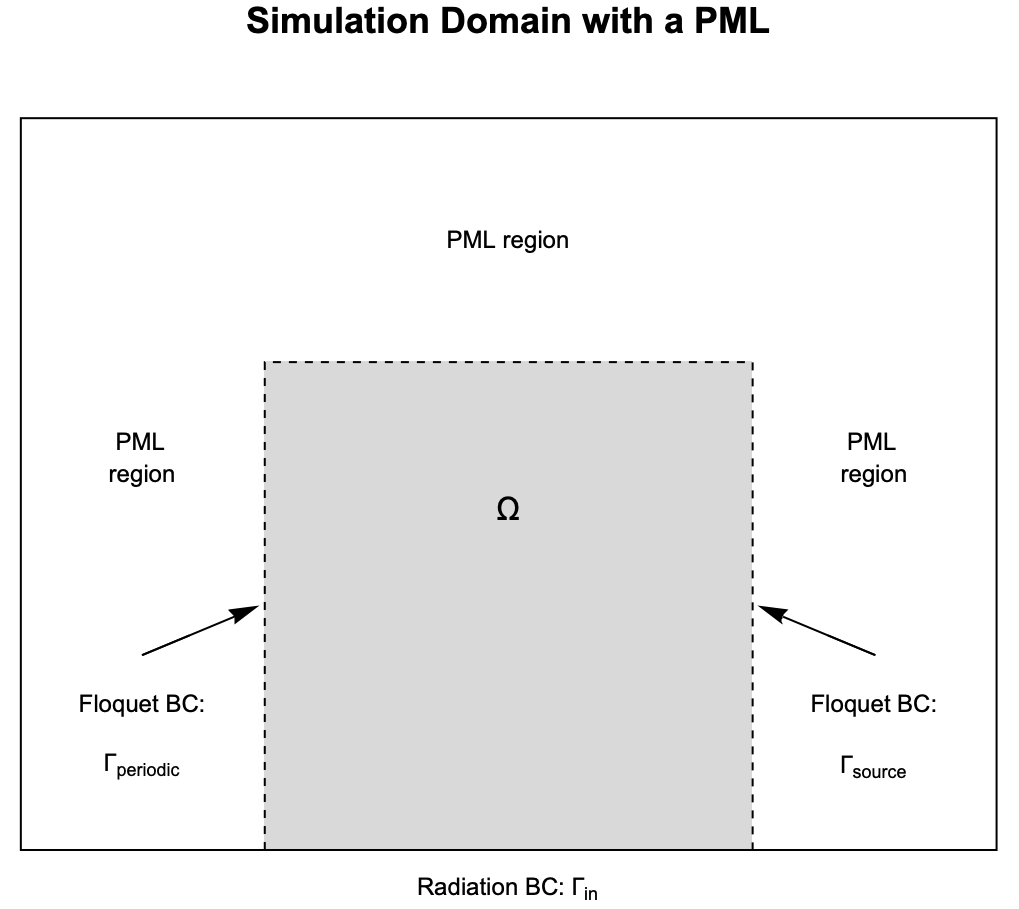
Furthermore, the outgoing wave though the boundaries needs to be simulated. In this case, an absorbing boundary condition is not applicable, due to the non-normal outbound angle. An alternative technique called "perfectly matched layer (PML)" is used instead. Further details on PML can be found in the following section entitled Perfectly Matched Layers (PML).
To implement a PML, the simulation domain is extended to include a PML region:
To set up the 2D domain that preserves the internal boundary between the regular domain ![]() and the PML region, the boundary mesh is generated manually. A detailed explanation about the mesh generation can be found in the Element Mesh Generation tutorial.
and the PML region, the boundary mesh is generated manually. A detailed explanation about the mesh generation can be found in the Element Mesh Generation tutorial.
In order to get a good result with PML implemented, a rid finer than the default is used for the mesh generation. Here the max edge length is set to be ![]() , which means that there will be at least 10 elements in the
, which means that there will be at least 10 elements in the ![]() (length) and
(length) and ![]() (width) directions of the domain
(width) directions of the domain ![]() .
.
Next, the Floquet periodic boundary condition is set up on the left edge. Note that the offset distance between the periodic boundary ![]() (left edge) and the source boundary
(left edge) and the source boundary ![]() (right edge) is
(right edge) is ![]() .
.
To simulate the inbound sound wave with an oblique incidence, a 2D radiation boundary condition is applied on the bottom edge of the domain.
See this note about improving the visual quality of the animation.
The animation shows a non-normal sound wave propagating over the domain. As the wave passes through the right boundary, it reappears on the left side, due to the spatial periodicity. Since the sound medium is assumed to be acoustic lossless, the magnitude of the wave remains at a constant level at all times.
Perfectly Matched Layer
A perfectly matched layer (PML) is a method to model simulation domains with infinite extent. As such, a PML is an alternative method to the absorbing boundary condition. The following section shows how to implement a PML for a Helmholtz PDE used in frequency domain modeling. The full derivation and the explanation can be found in the appendix section of the acoustics time domain tutorial.
To implement a PML, two things need to happen. First, the simulation domain needs to be enlarged. This extension is the region in which the PML is active. Second, a coordinate transformation of the PDE is done.
The three-dimensional Helmholtz equation after the PML coordinate transformation [50] is given by:
Here, ![]() ,
, ![]() and
and ![]() are the absorbing coefficients of the PML. Three auxiliary variables
are the absorbing coefficients of the PML. Three auxiliary variables ![]() ,
, ![]() and
and ![]() are introduced to control the PML attenuation in each dimension.
are introduced to control the PML attenuation in each dimension.
In the 1D case where ![]() , the equation (51) simplifies to:
, the equation (51) simplifies to:
The absorption coefficient ![]() is a tuning parameter to be chosen and is set to increase linearly within the PML layer from
is a tuning parameter to be chosen and is set to increase linearly within the PML layer from ![]() to
to ![]() . A thinner PML requires a greater value of
. A thinner PML requires a greater value of ![]() , but large
, but large ![]() tends to increase numerical reflections.
tends to increase numerical reflections.
The perfectly matched layer can be used with:
| analysis type | applicable | |
| Time Harmonic | Yes | |
| Eigenfrequency | No |
Perfectly Matched Layer in Time-Harmonic Analysis
As a next example, consider a simulation of a 1D domain from ![]() to
to ![]() using a computational domain that ranges from
using a computational domain that ranges from ![]() to
to ![]() with a PML at the right from
with a PML at the right from ![]() to
to ![]() .
.
As seen, ![]() in the original non-PML region.
in the original non-PML region.
The sound pressure in the non-PML region is fixed at the incident amplitude ![]() and then decays to zero within the PML region. To minimize the numerical reflection at the PML interface, the absorption coefficient
and then decays to zero within the PML region. To minimize the numerical reflection at the PML interface, the absorption coefficient ![]() and the PML width should be chosen carefully. The tradeoff between these two parameters is discussed in the acoustics time domain tutorial.
and the PML width should be chosen carefully. The tradeoff between these two parameters is discussed in the acoustics time domain tutorial.
The wave is attenuated within the PML but remains unchanged in the original domain, and the attenuation rate is independent of frequencies.
Nomenclature
| Symbol | Description | Unit |
| ρ | density of a medium | [kg/m3] |
| c | speed of sound in a medium | [m/s] |
| p | sound pressure | [Pa] |
| p | local sound amplitude | [Pa] |
| specified boundary pressure | [Pa] | |
| conjugate of sound pressure | [Pa] | |
| t | time | [s] |
| tend | simulation end time | [s] |
| X | position vector | [m] |
| s | direction switch | N/A |
| F | optional dipole source | [N/m3] |
| dipole source strength | [N/m3] | |
| θ | dipole directivity angle | [rad] |
| Q | optional monopole source | [1/s2] |
| monopole source strength | [1/s2] | |
| d | separation distance of dipole source | [m] |
| λ | wavelength of sound | [m] |
| Ω | simulation domain | [m] |
| k | wave number | [rad/m] |
| f | sound wave frequency | [Hz] |
| ω | sound wave angular frequency | [rad/s] |
| δ | Dirac delta function | N/A |
| regularized delta function | N/A | |
| γ | regularization parameter | [m] |
| h | mesh spacing | [m] |
| Xs | sound source location | [m] |
| κ | effective bulk modulus | [Pa] |
| α | attenuation factor | [m2/(s·N)] |
| ϕ | porosity | N/A |
| Vv | void volume | [m3] |
| VT | total volume | [m3] |
| Rf | flow resistivity | [kg/(m3·s)] |
| β | standard deviation of a Gaussian pulse | [m] |
| ζ | sound particle displacement | [m] |
| v | sound particle velocity | [m/s] |
| specified boundary velocity | [m/s] | |
| T | sound wave period | [t] |
| Z | characteristic impedence | [Pa·s/m] |
| Zb | boundary impedance | [Pa·s/m] |
| Ar | amplitude of reflected wave | [Pa] |
| Ai | amplitude of incident wave | [Pa] |
| σ | absorbtion coefficient of PML | [rad/(s·m)] |
| σmax | maximum value of absorbtion coefficient | [rad/(s·m)] |
References
1. Ihlenburg, F. "The Medium-Frequency Range in Computational Acoustics: Practical and Numerical Aspects." Journal of Computational Acoustics, Vol.11, No. 2 175-193, 2003.
2. Heutschi, K. Lecture Notes on Acoustics I. Swiss Federal Institute of Technology Zurich, 2016.
3. Johnson, S. "Notes on Perfectly Matched Layers (PMLs)." MIT, 2010.
4. Bilbao, S. and Hamilton, B. "Directional Source Modeling In Wave-Based Room Acoustics Simulation." IEEE, 2017.
5. Peskin, C. "The Immersed Boundary Method." Cambridge University, 2002.
6. Russell, D., Titlow, J. and Bemmen, Y.-J. "Acoustic Monopoles, Dipoles and Quadropoles: An Experiment Revisited." American Journal of Physics, 67, 660, 1999.
7. Vita, M. "The Wave Equation with a Source." Oklahoma State University.
8. De Moerloose, J. and Stuchly, M. A. "Behavior of Berenger's ABC for Evanescent Waves." IEEE Microwave and Guided Wave Letters, vol. 5, no. 10, pp. 344-346, Oct. 1995.
9. Berenger, J. "Evanescent Waves in PMLs: Origin of the Numerical Reflection in Wave-Structure Interaction Problems." IEEE Transactions on Antennas and Propagation, vol. 47, no. 10, pp. 1497-1503, Oct. 1999.
10. De Moerloose, J. and Stuchly, M. "Reflection Analysis of PML ABCs for Low-Frequency Applications." IEEE Microwave and Guided Wave Letters, vol. 6., no. 4, pp. 177-179, Apr. 1996.
11. Turkel, E. and Yefet, A. "Absorbing PML Boundary Layers for Wave-like Equations." Applied Numerical Mathematics, 27(4) 533-557, 1998.
12. Pan, G., Abubakar, A. and Habashy, T. "An Effective Perfectly Matched Layer Design for Acoustic Fourth-Order Frequency-Domain Finite-Difference Scheme." Geophysical Journal International, vol. 188, pp. 211-222, 2012.
13. Cox, T. and D'Antonio, P. Acoustic Absorbers and Diffusers: Theory, Design and Application. Spon Press, 2004.
14. Weisstein, E. W. "Fast Fourier Transform." MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/FastFourierTransform.html