Multiple Aperture Vector Diffraction
| Introduction | Nomenclature |
| Scalar Diffraction by Multiple Apertures | References |
| Vector Field Diffraction |
Introduction
Electromagnetic diffraction is a phenomenon that occurs when an electromagnetic (EM) wave passes trough an obstacle or aperture. For EM diffraction, the electric or magnetic field is described by a complex function. In the case of two or more apertures, the spatial distribution of the EM field after the aperture, called the diffraction pattern, is characterized by fringes that vary with the distance between apertures due to the spatial phase difference. This feature is greatly exploited in metrology to measure the distance of micro and nano objects.
In isotropic and non-dispersive media, diffraction of EM waves can be modeled by the vector-valued, source-free Helmholtz partial differential equation [Jackson, 1999]:
Here ![]() is the wave number in the medium
is the wave number in the medium ![]() and is related to the wavelength
and is related to the wavelength ![]() by
by ![]() . The wavelength in a medium
. The wavelength in a medium ![]() with refractive index
with refractive index ![]() is related to free space wavelength
is related to free space wavelength ![]() by
by ![]() . In some cases, only one component of the field is required to describe the full behavior of the field; in that case, the field is said to be scalar. The scalar case was studied in the "Single Aperture Scalar Diffraction" tutorial. This tutorial provides a brief introduction to multiple slits using a scalar approach, followed by a focus on the vector properties of EM waves.
. In some cases, only one component of the field is required to describe the full behavior of the field; in that case, the field is said to be scalar. The scalar case was studied in the "Single Aperture Scalar Diffraction" tutorial. This tutorial provides a brief introduction to multiple slits using a scalar approach, followed by a focus on the vector properties of EM waves.
Polarization is a property of transverse vector fields that specifies the geometric orientation of the oscillations. This property is exploited in a technique called polarimetry to characterize optically active samples.
As a prerequisite for the content presented here, it is recommended to work through the material presented in "Single Aperture Scalar Diffraction", as the basics of electromagnetic diffraction and perfectly matched layers are described there.
Many of the animations of the simulation results shown in this tutorial are generated with a call to Rasterize. This is to reduce the disk space this tutorial requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high-quality graphics, remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Scalar Diffraction by Multiple Apertures
Before modeling the vector Helmholtz equation (1), it will be useful to solve the simpler case of scalar diffraction by multiple apertures. This will help to introduce the boundary conditions and element mesh functionalities in a more understandable way.
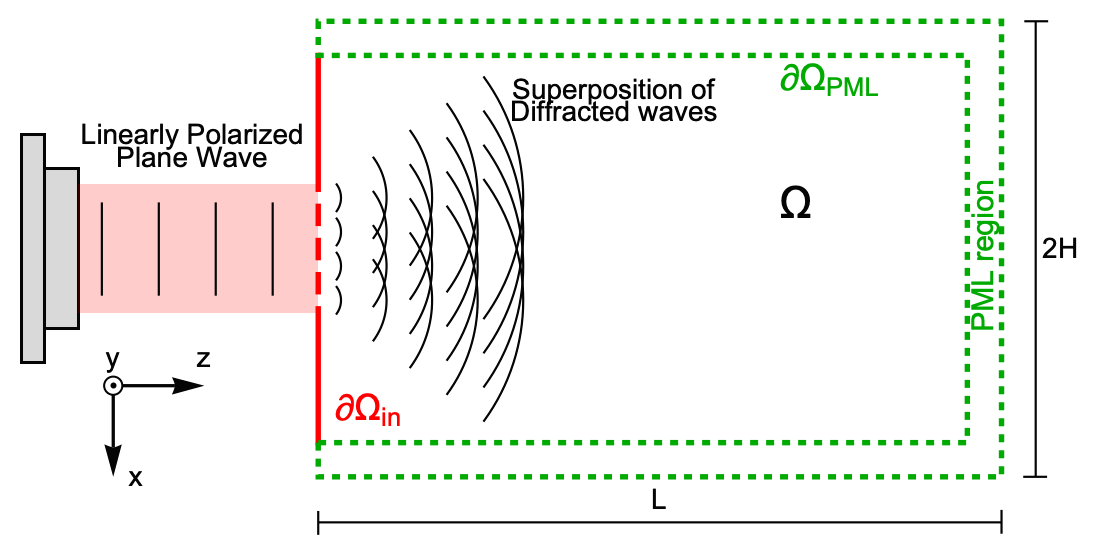
For this first example, consider a laser radiating an electromagnetic (EM) field propagating in the ![]() direction and polarized in the
direction and polarized in the ![]() direction. Under those conditions, the vector electric field can be considered as a scalar field containing energy only in the
direction. Under those conditions, the vector electric field can be considered as a scalar field containing energy only in the ![]() component [Born & Wolf, 1999].
component [Born & Wolf, 1999].
This application example considers a helium-neon laser with a free space wavelength ![]() illuminating an opaque screen with four evenly spaced apertures of width
illuminating an opaque screen with four evenly spaced apertures of width ![]() and separation
and separation ![]() . The apertures are slits assumed to be infinitely large in the
. The apertures are slits assumed to be infinitely large in the ![]() direction, so there will be no disturbances to the diffracted wave in the
direction, so there will be no disturbances to the diffracted wave in the ![]() direction; hence a system in 2D can be modeled. The laser and apertures themselves will be modeled by a radiation boundary condition on the
direction; hence a system in 2D can be modeled. The laser and apertures themselves will be modeled by a radiation boundary condition on the ![]() boundary. The opaque screen is made of a fully absorbing material where light cannot be transmitted or reflected. The boundary
boundary. The opaque screen is made of a fully absorbing material where light cannot be transmitted or reflected. The boundary ![]() indicates the beginning of the perfectly matched layer (PML) region. The PML region is an artificial boundary that absorbs incoming light to mimic an open system where light propagates indefinitely without any reflections [Jin, 1993]; therefore, the only source of light is the aperture, as the field is
indicates the beginning of the perfectly matched layer (PML) region. The PML region is an artificial boundary that absorbs incoming light to mimic an open system where light propagates indefinitely without any reflections [Jin, 1993]; therefore, the only source of light is the aperture, as the field is ![]() in the other boundaries. The simulation domain then has dimensions
in the other boundaries. The simulation domain then has dimensions ![]() and
and ![]() . The refractive index inside the propagation region
. The refractive index inside the propagation region ![]() is 1.
is 1.
The scheme above is rotated 90 degrees for better visualization; in the following, the propagation ![]() axis will be the vertical axis. Also note that the geometry is symmetric along the
axis will be the vertical axis. Also note that the geometry is symmetric along the ![]() direction and that the
direction and that the ![]() direction points outward from the screen.
direction points outward from the screen.
Domain
To make use of the PML approach, the propagation region ![]() has to be extended by an extra layer of length
has to be extended by an extra layer of length ![]() which will be the PML region. In this region, the incoming wave will be damped out.
which will be the PML region. In this region, the incoming wave will be damped out.
Boundaries 1 and 3 (dotted green) describe the outer and inner boundaries of the PML region. Boundaries with marker 4 (orange) are needed to set up the PML parameters. The boundary 2 (red) describes the opaque screen and apertures. To distinguish between the opaque screen and apertures, a function will be used inside the Neumann boundary condition.
From the "Single Aperture Scalar Diffraction" tutorial, it is observed that the intensity profiles in regions far from the ![]() axis are negligible. A MeshRefinementFunction can be utilized to create a finer mesh at specified coordinates, and "RegionMarker" can be used to divide the PML region into four subregions. In 2D, a MeshRefinementFunction operates based on the element's area. The area of a triangle in the mesh can be approximated using the formula for the area of an equilateral triangle, which is
axis are negligible. A MeshRefinementFunction can be utilized to create a finer mesh at specified coordinates, and "RegionMarker" can be used to divide the PML region into four subregions. In 2D, a MeshRefinementFunction operates based on the element's area. The area of a triangle in the mesh can be approximated using the formula for the area of an equilateral triangle, which is ![]() , where
, where ![]() represents the edge length of the triangle.
represents the edge length of the triangle.
It is worth mentioning that ![]() is a recommended initial discretization constraint to properly resolve the EM wave [Jin, 1993]. In some systems, a smaller constant has to be used to provide a precise result.
is a recommended initial discretization constraint to properly resolve the EM wave [Jin, 1993]. In some systems, a smaller constant has to be used to provide a precise result.
Now, create the mesh with a maximum element area depending on the position. In the region ![]() , the recommended edge length is used, as it is the region of interest. Outside that region, the field is practically 0. Therefore, a larger edge length is used to reduce the number of unknowns for the FEM method.
, the recommended edge length is used, as it is the region of interest. Outside that region, the field is practically 0. Therefore, a larger edge length is used to reduce the number of unknowns for the FEM method.
The use of Rasterize above helps to reduce the size of the graphics. For a better visual appearance, the Rasterize can be removed.
Parameters Setup
The basics of PML are described in the acoustic time and frequency domain tutorials. Roughly speaking, a PML region mimics an absorbing material with an absorbing coefficient ![]() . While
. While ![]() is set inside the propagation region
is set inside the propagation region ![]() , an increasing function with maximum value
, an increasing function with maximum value ![]() is set inside the PML region [Jin, 1993] and there dampens the wave out.
is set inside the PML region [Jin, 1993] and there dampens the wave out.
The use of Rasterize above helps to reduce the size of the graphics. For a better visual appearance, the Rasterize can be removed.
In the ![]() plots, it is evident that the absorbing coefficient behaves as a wall in each direction outside the region
plots, it is evident that the absorbing coefficient behaves as a wall in each direction outside the region ![]() , while it does not alter the electric field inside the region
, while it does not alter the electric field inside the region ![]() .
.
Boundary Conditions
The incoming wave illuminating the boundary ![]() containing the opaque screen and aperture can be modeled with a radiation boundary condition of the form [Jin, 1993]:
containing the opaque screen and aperture can be modeled with a radiation boundary condition of the form [Jin, 1993]:
with ![]() the boundary normal,
the boundary normal, ![]() the incoming EM wave propagation direction and
the incoming EM wave propagation direction and ![]() the EM wave amplitude. The boundary condition is a sum of two terms, a light incidence term
the EM wave amplitude. The boundary condition is a sum of two terms, a light incidence term ![]() and an absorbing boundary condition term
and an absorbing boundary condition term ![]() .
.
The second term is needed to ensure that the boundary ![]() does not reflect EM waves and only the incident light flows outward from the boundary. In this case, both the boundary normal and the wave propagation direction are in the
does not reflect EM waves and only the incident light flows outward from the boundary. In this case, both the boundary normal and the wave propagation direction are in the ![]() direction; therefore the inner product is 1.
direction; therefore the inner product is 1. ![]() will be used to distinguish between the screen and apertures. From equation (2), it is evident that setting
will be used to distinguish between the screen and apertures. From equation (2), it is evident that setting ![]() to 0 results in only the absorbing term, which represents an opaque screen. However, setting
to 0 results in only the absorbing term, which represents an opaque screen. However, setting ![]() to
to ![]() represents an aperture with an initial amplitude of
represents an aperture with an initial amplitude of ![]() .
.
where ![]() is the number of apertures,
is the number of apertures, ![]() is the width of each aperture and
is the width of each aperture and ![]() the distance between the centers of any two apertures.
the distance between the centers of any two apertures.
Now, set up the radiation boundary condition with the following parameters: ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
Model Evaluation
Visualization
See this note about improving the visual quality of the animation.
Model Verification
Next, the solution is validated against an analytical solution. To verify the model, the integral diffraction formula deduced by Green's method [Ishimarou, 1991] can be used. In 2D, the analytical solution is as follows:
where ![]() is the Euclidian distance between any point
is the Euclidian distance between any point ![]() at
at ![]() and a point
and a point ![]() inside the region
inside the region ![]() . As the aperture is a line, the normal is a vector in the
. As the aperture is a line, the normal is a vector in the ![]() direction. For a detailed deduction, see [Ishimarou, 1991].
direction. For a detailed deduction, see [Ishimarou, 1991].
A more detailed discussion about the analytical solution is given in the "Single Aperture Scalar Diffraction" tutorial.
Vector Field Diffraction
In the preceding section, the diffraction of scalar fields through an object was described. Scalar fields have a single value at each point in space. On the other hand, vector fields have an amplitude and a direction, therefore the field ![]() can be written as
can be written as ![]() , with
, with ![]() the amplitude and
the amplitude and ![]() the orientation or polarization angle.
the orientation or polarization angle.
In a medium with a diagonal relative permittivity tensor ![]() , the components of the electric field
, the components of the electric field ![]() are independent and can be solved individually [Born & Wolf, 1999].
are independent and can be solved individually [Born & Wolf, 1999].
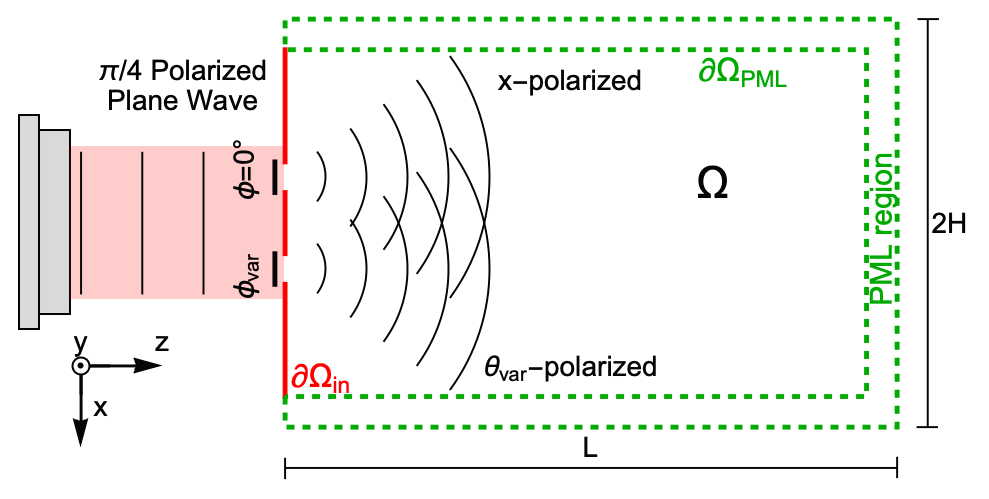
In the following, the diffraction of a vector field will be modeled by two apertures with a linear polarizer in each one. A linear polarizer is an optical filter instrument that only allows EM waves with a specific polarization angle ![]() to pass through. The polarizer angle
to pass through. The polarizer angle ![]() is called the transmission axis.
is called the transmission axis.
For example, when an EM wave with a polarization angle ![]() passes through a linear polarizer with transmission axis
passes through a linear polarizer with transmission axis ![]() , the EM wave polarization angle after the polarizer will be
, the EM wave polarization angle after the polarizer will be ![]() , but with a reduced intensity. The intensity will be
, but with a reduced intensity. The intensity will be ![]() , and the remaining intensity will be absorbed by the polarizer. This is called Malus's law. One important note is that if
, and the remaining intensity will be absorbed by the polarizer. This is called Malus's law. One important note is that if ![]() and
and ![]() are orthogonal (
are orthogonal (![]() ), the final intensity will be zero.
), the final intensity will be zero.
A linear polarizer with transmission axis ![]() is characterized by a transmission matrix [Born & Wolf, 1999].
is characterized by a transmission matrix [Born & Wolf, 1999].
Assume that the linear polarizer located at the upper aperture is fixed at ![]() , i.e. only the
, i.e. only the ![]() component of the incident field passes through the aperture. The other polarizer located at the lower aperture has a variable transmission axis
component of the incident field passes through the aperture. The other polarizer located at the lower aperture has a variable transmission axis ![]() .
.
The scheme above is rotated 90 degrees for better visualization; in the following, the propagation ![]() axis will be the vertical axis. Also note that the
axis will be the vertical axis. Also note that the ![]() direction points outward from the screen.
direction points outward from the screen.
Parameter Setup
Set up the vector Helmholtz operator for the field ![]() and the diagonal anisotropic (orthotropic) permittivity
and the diagonal anisotropic (orthotropic) permittivity ![]() for the PML region. In this case, an additional
for the PML region. In this case, an additional ![]() rank-3 tensor is needed to set up both PDEs simultaneously. See the DiffusionPDETerm reference page for more information.
rank-3 tensor is needed to set up both PDEs simultaneously. See the DiffusionPDETerm reference page for more information.
Domain Definition
The same domain, ElementMesh and PML parameters are used as for the 2D PML scalar example presented above.
Boundary Conditions
Before establishing the boundary conditions for the apertures with the linear polarizers, an auxiliary function for the polarizer transmission matrix needs to be created.
Now, the same approach as in the scalar example can be used. Set up a function for the amplitude ![]() for each aperture. In this case, the amplitude is not a scalar; it is a 2D vector. A linear polarizer is placed in each aperture, one with a transmission axis at 0° and the other has an arbitrary transmission axis
for each aperture. In this case, the amplitude is not a scalar; it is a 2D vector. A linear polarizer is placed in each aperture, one with a transmission axis at 0° and the other has an arbitrary transmission axis ![]() . The transmission matrix needs to be multiplied to the incoming vector field amplitude.
. The transmission matrix needs to be multiplied to the incoming vector field amplitude.
![]() is the width and
is the width and ![]() is the spacing between the two apertures' center.
is the spacing between the two apertures' center.
See this note about improving the visual quality of the animation.
Model Evaluation
For this example, the same mesh element and PML regions employed in the 2D PML example will be used.
Now, do a sweep for different values of ![]() between
between ![]() and
and ![]() .
.
See this note about improving the visual quality of the animation.
When ![]() , both apertures have the same polarization and a result is obtained equal to the scalar case studied previously. When
, both apertures have the same polarization and a result is obtained equal to the scalar case studied previously. When ![]() starts increasing, the
starts increasing, the ![]() component of the EM wave going out of the upper aperture will interfere with the
component of the EM wave going out of the upper aperture will interfere with the ![]() component of the EM wave going out of the lower aperture. The amount of energy in the
component of the EM wave going out of the lower aperture. The amount of energy in the ![]() component varies with
component varies with ![]() . On the other hand, the EM wave going out of the upper aperture does not contain energy in the
. On the other hand, the EM wave going out of the upper aperture does not contain energy in the ![]() component, therefore the
component, therefore the ![]() component of the EM wave going out of the lower aperture does not interfere with anything, producing a single slit pattern whose magnitude varies with
component of the EM wave going out of the lower aperture does not interfere with anything, producing a single slit pattern whose magnitude varies with ![]() . When
. When ![]() , the fields diffracted at the upper and lower apertures are orthogonal, therefore showing two single-aperture patterns.
, the fields diffracted at the upper and lower apertures are orthogonal, therefore showing two single-aperture patterns.
The intensity of the field will be proportional to the sum of the squares of all the components, i.e. ![]() .
.
Nomenclature
| Symbol | Description | Unit |
| E | Electric field | [V/m] |
| λn | Wavelength | [m] |
| kn | Wavenumber | [1/m] |
| μr | Relative permeability | N/A |
| ϵr | Relative permittivity | N/A |
| L | Propagation region length | [μm] |
| H | Propagation region width | [μm] |
| d | Aperture size | [m] |
| ϕ | Aperture size | [m] |
| Γscreen | Opaque screen boundary | N/A |
| Γaperture | Aperture boundary | N/A |
| ΓABC | Absorbing boundary | N/A |
| Γin | Screen and aperture boundary | N/A |
| Ω | Computational domain | N/A |
References
1. Born, M. and Wolf, E.(1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (7th ed.). Cambridge: Cambridge University Press.
2. Jackson, J. D. Classical Electrodynamics. New York: Wiley, 1999.
3. Jin, J.-M. The Finite Element Method in Electromagnetics. John Wiley & Sons, 2015.
4. A. Ishimarou. Electromagnetic Wave Propagation, Radiation, and Scattering. Prentice Hall, 1991.