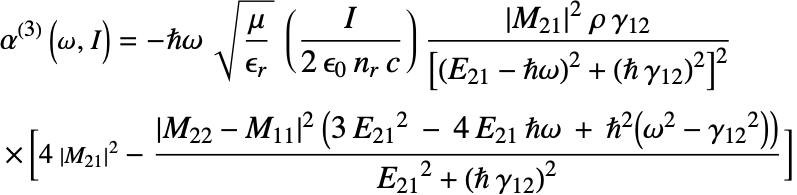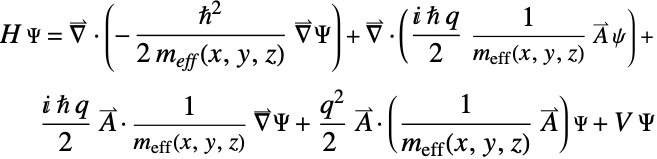Quantum Ring
Introduction
Semiconductor quantum dots (QDs) [Garcia, 2021] are structures made from the union of two or more semiconductor materials, like ![]() or
or ![]() , and are fabricated so their geometry has dimensions on the order of 100 nanometers or less. Due to the difference in energy gaps between each of the semiconductor materials forming the QD, they restrict the mobility of charge carriers like electrons or holes in all three dimensions and, effectively, confine them inside the QD. They exhibit properties that are normally associated with atoms, such as quantized energy levels. For this reason, QDs are sometimes called artificially fabricated atoms. The nature of the charge carriers confined inside QDs is described by the wavefunction that is obtained by solving the Schrödinger equation.
, and are fabricated so their geometry has dimensions on the order of 100 nanometers or less. Due to the difference in energy gaps between each of the semiconductor materials forming the QD, they restrict the mobility of charge carriers like electrons or holes in all three dimensions and, effectively, confine them inside the QD. They exhibit properties that are normally associated with atoms, such as quantized energy levels. For this reason, QDs are sometimes called artificially fabricated atoms. The nature of the charge carriers confined inside QDs is described by the wavefunction that is obtained by solving the Schrödinger equation.
Quantum rings (QRs) are a type of QD that were first fabricated by Granados et al. [Granados, 2003] in 2003. Since their appearance, QRs have been a focus of many condensed matter physicists. They have been proven to be useful in many applications, like lasers [Cao, 2005], quantum computing [Yu, 2008] and single-photon emission [Gallardo, 2010], and there are still other studies that show promising qualities for other applications like optoelectronics [Fomin, 2014].
In many of the studies in the literature, the authors consider two-dimensional QRs like the one by Xie [Xie, 2009], but very few consider the 3D nature of the QRs. This represents one of the advantages that the finite element method has for solving the Schrödinger equation in QDs with rich 3D geometry like QRs.
In this example, a mono-electronic system confined in a quantum ring is considered. The ring is composed of ![]() , while the surroundings are made of
, while the surroundings are made of ![]() . The objective is to find the eigenstates, which can be the starting point for further calculations like optical absorption and thermodynamical properties, among others.
. The objective is to find the eigenstates, which can be the starting point for further calculations like optical absorption and thermodynamical properties, among others.
An electron inside the QR will experience a finite step confinement potential, which means that inside the ring, the potential would be 0, and a finite constant potential outside the ring. In standard conditions of pressure and temperature, the potential outside the QR would be of 256.8 meV, when the concentration aluminum is ![]()
![]() [Culchac, 2009].
[Culchac, 2009].
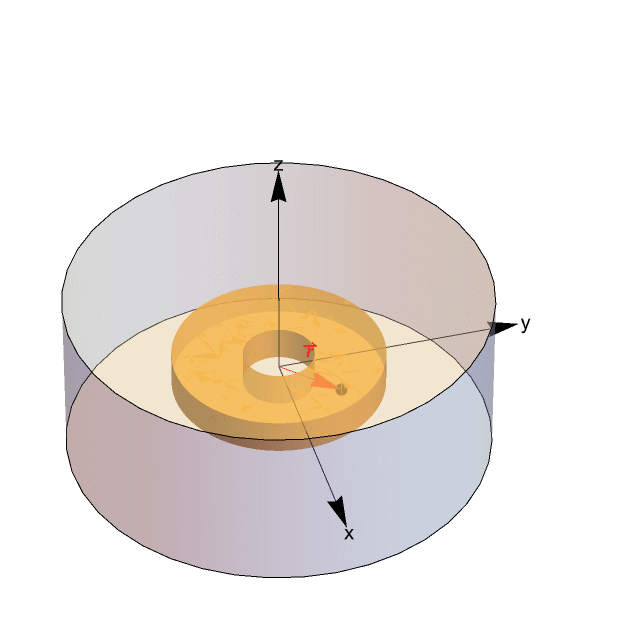
Depiction of the quantum ring and its surroundings. Here the ![]() vector represents the position of the electron in the Schrödinger equation.
vector represents the position of the electron in the Schrödinger equation.
The behavior of charge carriers inside a crystalline semiconductor, like an electron or a hole, is described by the theory of solid-state physics [Ashcroft, 1976]. In particular, the motion of these particles is described by band theory [Zawadzki, 2020]. In this context, a quantity that is analogous to the electron mass is defined. It is called the effective mass, and it helps describe how a particle in a periodic potential, such as an electron in a crystal, would respond to external forces, taking into account all the interactions that the particle is submitted to inside the crystal. This is a topic with many nuances, for instance, see [Chang, 2014][Duque-Gomez, 2012].
Generally speaking, the effective mass can depend on position and other factors such as temperature and pressure. For this example, as a first approach, a simplification widely used in the literature can be considered. This simplification states that for electrons or holes with a small crystal momentum, the effective mass can be regarded as constant [Zawadzki, 2020]. According to Kohn and Sham [Kohn-Sham, 1965], the numerous interactions within the crystal that each electron experiences can be approximated by a single average potential. This transforms a many-electron problem into a one-electron Schrödinger equation. Additionally, the envelope function approximation can be applied [Harrison, 2005], allowing the time-independent Schrödinger equation for the electron's wavefunction to be written as in equation 1.
The time-independent Schrödinger equation for the electron's wavefunction is given as:
Here ![]() represents the effective mass of the electron. For
represents the effective mass of the electron. For ![]() ,
, ![]() ,
, ![]() being the free electron's mass. Also in this case, the potential
being the free electron's mass. Also in this case, the potential ![]() is a piecewise function that defines a potential energy of
is a piecewise function that defines a potential energy of ![]() outside the ring and
outside the ring and ![]() inside it.
inside it.
Parameters
The ring's mean radius ![]() , width
, width ![]() , height of the ring
, height of the ring ![]() , boundary radius
, boundary radius ![]() and the height of the whole region
and the height of the whole region ![]() are defined, which all represent distances in nanometers.
are defined, which all represent distances in nanometers.
These geometric parameters for this example are inspired by similar theoretical work considering a square cross section quantum ring [Hernandez, 2022].
Domain
It is necessary to load the NDSolve FEM package.
One region is created for the ring and another for the bounding domain.
Next, a region is created by taking the difference between the two regions created above. This results in a hollow part inside the domain, which will define the ring in the mesh later on.
For generating the mesh, the "RegionMarker" option is used to set different mesh element sizes in the two different regions, as well as "RegionHoles"->None, such that ring is part of the mesh too.
Hamiltonian and Confinement Potential
Potential
A finite step potential is defined such that the potential energy is ![]() outside the ring and
outside the ring and ![]() inside it. The value of the potential is given without units for now, and units will be incorporated later when defining the Hamiltonian.
inside it. The value of the potential is given without units for now, and units will be incorporated later when defining the Hamiltonian.
The SetDelayed statement does not evaluate the right-hand side; as a consequence, in every call to the function V, the ringMemberFunction will need to be evaluated. That makes the process of solving the differential equation inefficient. So, the Evaluate function is used in the definition of the potential to make the whole process more efficient. Consider reading this section on efficient evaluation of PDE coefficients for more details.
Hamiltonian
First, the effective mass and the reduced Planck constant are defined.
Next, the units of the potential are specified with the Quantity function. Since the dimensions of the geometry are in nanometers, the parameter "ScaleUnits"{"Meters""Nanometers"} is set so that all units are consistent.
In the next step, the Schrödinger PDE component is used to generate all the PDE terms.
Boundary Conditions
One Dirichlet condition is imposed, requiring the electron's wavefunction for the low-lying states of interest to decay to ![]() at a significant distance from the ring. This is achieved by setting the wavefunction to
at a significant distance from the ring. This is achieved by setting the wavefunction to ![]() at the outer boundary of the previously defined domain.
at the outer boundary of the previously defined domain.
Solving the Eigenvalue Problem
Now, NDEigensystem is used to solve the eigenvalue problem with the Hamiltonian ![]() and the mesh previously defined. The variables en and funs are defined as the energy eigenvalues and the wavefunctions, respectively.
and the mesh previously defined. The variables en and funs are defined as the energy eigenvalues and the wavefunctions, respectively.
It takes less than ![]() minute to find
minute to find ![]() eigenstates with a normal laptop.
eigenstates with a normal laptop.
Visualization
To interpret the units of the eigenvalues, it is essential to note that the SchrodingerPDEComponent internally converts all units to SI units. When specifying "ScaleUnits"{"Meters""Nanometers"} in the parameters pars, all units of meters are converted to nanometers. Thus, the reverse procedure is followed to convert back to millielectronvolts.
It is clear that the second and third eigenvalues are numerically identical, and the same goes for the fourth and fifth values. This makes sense because these are degenerate eigenstates. Degenerate eigenvalues are expected when the system has symmetry, like the rotational symmetry of the quantum ring. This is easier to see by looking at the corresponding probability densities.
The probability density for the second and third states is basically the same but rotated around the ![]() axis, as can be seen from the top view. This is because states
axis, as can be seen from the top view. This is because states ![]() and
and ![]() , as well as
, as well as ![]() and
and ![]() , form a degenerate subspace, meaning that any linear combination of those states would lead to a valid solution.
, form a degenerate subspace, meaning that any linear combination of those states would lead to a valid solution.
Also, one important feature is that by making use of NDEigensystem, one obtains the wavefunctions already normalized.
On the other hand, it is possible to take a closer look at each eigenfunction by doing a contour plot.
Magnetic Field Interaction
The effect of an external magnetic field on the eigenstates describing particles confined in low-dimensional systems, such as QDs and QRs, is something that has been considered by various authors [Jahan, 2018], [Gutiérrez, 2010]. One of the reasons this is an area of interest is that the interaction with the magnetic field can greatly affect the energy spectrum and as a consequence, the transition energy between the states confined in the nanostructure. Also, a periodic oscillation in the eigenvalues for each state as the magnetic flux density is increased can be observed, a phenomenon known as Aharanov–Bohm (AB) oscillations. In particular, AB oscillations are present for particles confined in a QR submitted to the presence of a threading magnetic field [Fomin, 2018]. For this reason, an external constant magnetic field pointing in the ![]() direction will be considered.
direction will be considered.
Usually, the Hamiltonian operator for a particle of mass ![]() has the following form:
has the following form: ![]() , where
, where ![]() is the momentum operator that in quantum mechanics is defined as
is the momentum operator that in quantum mechanics is defined as ![]() . On the other hand, by following what is known as Peierl's substitution [Luttinger, 1951][Peierls, 1997], when a magnetic field is present, the momentum changes from
. On the other hand, by following what is known as Peierl's substitution [Luttinger, 1951][Peierls, 1997], when a magnetic field is present, the momentum changes from ![]() to
to ![]() , where
, where ![]() is the magnetic vector potential, which is defined in such a way that one can obtain the magnetic flux density as
is the magnetic vector potential, which is defined in such a way that one can obtain the magnetic flux density as ![]() .
.
Therefore, the Hamiltonian takes the following form:
The term ![]() can be expanded as
can be expanded as ![]() , and therefore, the Hamiltonian would take the form in equation 2.
, and therefore, the Hamiltonian would take the form in equation 2.
Now, applying the definition of ![]() , replacing
, replacing ![]() for the effective mass and
for the effective mass and ![]() for the electron's charge, the PDE operator acquires the following form.
for the electron's charge, the PDE operator acquires the following form.
One particular characteristic of the magnetic vector potential is that one can add the gradient of a scalar function, for instance ![]() , to
, to ![]() as
as ![]() , and it would lead to the same magnetic flux density, since
, and it would lead to the same magnetic flux density, since ![]() . The function
. The function ![]() is called a gauge function, and choosing a particular
is called a gauge function, and choosing a particular ![]() and
and ![]() is called gauge fixing. This choice can, in many cases, lead to a simplification of the equations involved. One common way to do this is to use Coulomb's gauge fixing condition, which states that
is called gauge fixing. This choice can, in many cases, lead to a simplification of the equations involved. One common way to do this is to use Coulomb's gauge fixing condition, which states that ![]() .
.
As a justification of this condition, consider an original vector potential, ![]() , which divergence does not make vanish, i.e
, which divergence does not make vanish, i.e ![]() . Then add to it the gradient of a scalar function such that
. Then add to it the gradient of a scalar function such that ![]() . This way, Coulomb's condition,
. This way, Coulomb's condition, ![]() , would lead to the equation
, would lead to the equation ![]() . This is a Poisson-type equation and it has a unique solution. Therefore,
. This is a Poisson-type equation and it has a unique solution. Therefore, ![]() would be uniquely determined by applying the condition
would be uniquely determined by applying the condition ![]() . That means that Coulomb's gauge fixing condition can always be applied without any ambiguity. In summary, since the curl of
. That means that Coulomb's gauge fixing condition can always be applied without any ambiguity. In summary, since the curl of ![]() is specified by
is specified by ![]() but the divergence of
but the divergence of ![]() is not specified, it is possible to set the divergence of
is not specified, it is possible to set the divergence of ![]() in a way that simplifies the equations, in this case
in a way that simplifies the equations, in this case ![]() .
.
Considering Coulomb's gauge fixing condition, the PDE operator can be written as shown in equation 3:
A magnetic vector potential is considered that satisfies the condition that ![]() , where
, where ![]() is the position vector, which ensures that
is the position vector, which ensures that ![]() is true. Then the SchrodingerPDEComponent is used to generate the new PDE operator.
is true. Then the SchrodingerPDEComponent is used to generate the new PDE operator.
Note that QuantityMagnitude is used in order to ensure that the SchrodingerPDEComponent can handle correctly the units of ![]() .
.
To generate the PDE operator, specify the magnetic vector potential and the charge of the particle in the parameters argument of the SchrodingerPDEComponent function. This way, two additional terms are added to the PDE.
Activate was used to show how ultimately the PDE operator given by the SchrodingerPDEComponent is consistent with equation 4.
Note that the Coulomb's gauge for the magnetic vector potential, i.e ![]() , is satisfied by the specific selection of
, is satisfied by the specific selection of ![]() .
.
Solving the Eigenvalue Problem
Next, the eigenvalue problem can be solved using the same mesh and boundary conditions as before.
Visualization
The presence of the magnetic field makes the wavefunctions complex valued, and it is necessary to separate the real and imaginary parts of the resulting interpolating function to plot it using the Abs function.
The obtained eigenvalues are complex numbers, as the PDE is now complex valued in nature.
Upon close inspection, one can see that the imaginary part is very small compared with the real part, and one can suspect that this is due to numerical noise, given the fact that in quantum mechanics the energy eigenvalues are always a real quantity. For this reason, the real part of the eigenvalues obtained with NDEigensystem will be considered.
Comparing the real part of the eigenvalues with and without the magnetic field reveals that states ![]() and
and ![]() , as well as
, as well as ![]() and
and ![]() , are no longer degenerate. Thus, the presence of the magnetic field removes the degeneracy of the eigenstates observed when no magnetic field was present.
, are no longer degenerate. Thus, the presence of the magnetic field removes the degeneracy of the eigenstates observed when no magnetic field was present.
Varying the Magnetic Field
To explore how the external magnetic field affects the energy eigenvalues, the energy of each state can be calculated as a function of the magnetic flux density. This can be done by just redefining the PDE operator and solving the eigenvalue problem for each value of the magnetic flux density. For this purpose, a function is defined.
Then Table is used to find the energy for a range of magnetic flux densities.
This is a lengthy calculation and takes about ![]() minutes to complete with the current mesh on a normal laptop.
minutes to complete with the current mesh on a normal laptop.
The last graph represents the AB oscillations of the energy levels, as is often referred to in the literature. One important feature is that the degeneracy in the eigenstates that can be seen when no magnetic field is present at ![]() is revoked by the presence of the magnetic field. The energy levels then begin to split as the magnetic flux density is increased, a phenomenon known as the Zeeman effect. Furthermore, from the graph, it is clear that the energy of the lowest state starts to grow until a point near
is revoked by the presence of the magnetic field. The energy levels then begin to split as the magnetic flux density is increased, a phenomenon known as the Zeeman effect. Furthermore, from the graph, it is clear that the energy of the lowest state starts to grow until a point near ![]() , where subsequently it starts to fall and then increases again at a point near
, where subsequently it starts to fall and then increases again at a point near ![]() . This oscillation is also present for the remaining states. For instance, the energy of the next state starts decreasing until near
. This oscillation is also present for the remaining states. For instance, the energy of the next state starts decreasing until near ![]() , when it starts to increase up to a point close to
, when it starts to increase up to a point close to ![]() , from which it falls back again. And a similar pattern is present for higher states.
, from which it falls back again. And a similar pattern is present for higher states.
In summary, a key feature is that that the mere presence of the magnetic field makes the eigenstates no longer degenerate.
On the other hand, something worth noting in the graph is the "anti-crossing" or "avoided crossing" in the energy levels. For instance, take the point close to ![]() where the eigenvalues for the first two states come really close and seem to "avoid" each other afterward. This is a common feature of quantum systems, when two eigenvalues will not cross when the strength of a perturbation, as is the case of the magnetic field, is increased [Cohen-Tannaoudji, 1992].
where the eigenvalues for the first two states come really close and seem to "avoid" each other afterward. This is a common feature of quantum systems, when two eigenvalues will not cross when the strength of a perturbation, as is the case of the magnetic field, is increased [Cohen-Tannaoudji, 1992].
To explore the effect that the external field has on the wavefunctions, the probability densities are plotted for a magnetic flux density of ![]() . The choice of that specific value will be clear later.
. The choice of that specific value will be clear later.
Taking into account the steps in which the magnetic flux density was varied in the previous calculation, the wavefunctions and eigenvalues for a magnetic flux density of ![]() can be obtained.
can be obtained.
These last energies are the real part of the eigenvalues provided by NDEigensystem in millielectronvolts.
There are a few things that one can notice here. First, the wavefunctions for states ![]() and
and ![]() have interchanged roles compared with the wavefunctions previously calculated for a magnetic flux density of
have interchanged roles compared with the wavefunctions previously calculated for a magnetic flux density of ![]() . And the same can be said about states
. And the same can be said about states ![]() and
and ![]() . Moreover, the wavefunction for state
. Moreover, the wavefunction for state ![]() has a morphology that did not appear in the first five states for the
has a morphology that did not appear in the first five states for the ![]() case. To explain this, its useful to analyze the AB oscillations graph.
case. To explain this, its useful to analyze the AB oscillations graph.
The AB oscillations pattern can be understood as a set of displaced parabolas, each representing a state. This way, the energy for a particular eigenstate at ![]() , with its correspondent wavefunction, will evolve following a parabola. In the case of
, with its correspondent wavefunction, will evolve following a parabola. In the case of ![]() , the probability densities morphologies are the same as in the no magnetic field case, which can be understood by looking at the last figure and noticing that the ordering of the eigenstates is the same for a value of
, the probability densities morphologies are the same as in the no magnetic field case, which can be understood by looking at the last figure and noticing that the ordering of the eigenstates is the same for a value of ![]() as for a
as for a ![]() case. Inversely, for the case with magnetic flux density of
case. Inversely, for the case with magnetic flux density of ![]() , the parabolas have intertwined, and as a consequence, the ordering of the eigenstates has changed, which is reflected in the probability densities as described earlier. Furthermore, state
, the parabolas have intertwined, and as a consequence, the ordering of the eigenstates has changed, which is reflected in the probability densities as described earlier. Furthermore, state ![]() in the
in the ![]() case can be traced back, following a parabola, up to the point with a magnetic flux density of
case can be traced back, following a parabola, up to the point with a magnetic flux density of ![]() , and, as can be seen in the previous graph, in that case it would correspond to state
, and, as can be seen in the previous graph, in that case it would correspond to state ![]() . That is the reason why in the morphology of the probability density for state
. That is the reason why in the morphology of the probability density for state ![]() in the
in the ![]() case differs from the previously studied cases.
case differs from the previously studied cases.
The choice of the specific magnetic flux density of ![]() is clearer now. Any value between
is clearer now. Any value between ![]() and
and ![]() would reveal how the states have intertwined and how the wavefunctions have interchanged order due to the presence of the magnetic field, as can be seen in the graph.
would reveal how the states have intertwined and how the wavefunctions have interchanged order due to the presence of the magnetic field, as can be seen in the graph.
Optical Absorption
Once the eigenstates are computed, additional properties such as the optical absorption can be obtained. To calculate the optical absorption, the first two eigenstates obtained for a magnetic flux density of ![]() are considered.
are considered.
The presence of a magnetic field will be included in the optical absorption calculation because, without it, states ![]() and
and ![]() are degenerate, which means that the real physical system will be in a linear combination of the two. Therefore, the magnetic field's ability to remove the degeneracy of the eigenstates will be utilized. And in this case, a magnetic flux density of
are degenerate, which means that the real physical system will be in a linear combination of the two. Therefore, the magnetic field's ability to remove the degeneracy of the eigenstates will be utilized. And in this case, a magnetic flux density of ![]() will be sufficient to have the first two eigenstates be non-degenerate.
will be sufficient to have the first two eigenstates be non-degenerate.
One way to compute the optical absorption is to follow a procedure described by Karabulut et al. [Karabulut, 2005] that is based on the density matrix formalism and perturbation theory. The details on how the interaction with light is modeled are in Karabulut's paper [Karabulut, 2005]. The expressions for the linear optical absorption ![]() , the nonlinear optical absorption
, the nonlinear optical absorption ![]() and total optical absorption
and total optical absorption ![]() that are given in equations 5, 6 and 7, respectively, can then be applied.
that are given in equations 5, 6 and 7, respectively, can then be applied.
Here, ![]() is the permeability of
is the permeability of ![]() and
and ![]() and
and ![]() are vacuum and relative electrical permittivity, respectively. The intensity of the incident light beam is
are vacuum and relative electrical permittivity, respectively. The intensity of the incident light beam is ![]() , and
, and ![]() is its frequency. The
is its frequency. The ![]() is the inverse of the decay time between states 1 and 2, due to the interaction between the system and the environment.
is the inverse of the decay time between states 1 and 2, due to the interaction between the system and the environment. ![]() is the carrier density of states of
is the carrier density of states of ![]() ,
, ![]() is the refractive index, and
is the refractive index, and ![]() is the speed of light.
is the speed of light. ![]() are the components of the electric dipole matrix defined as
are the components of the electric dipole matrix defined as ![]() , where
, where ![]() is the electron's charge and
is the electron's charge and ![]() represents the
represents the ![]() coordinate, which is also in the direction in which the incident light beam is polarized. And finally,
coordinate, which is also in the direction in which the incident light beam is polarized. And finally, ![]() is the difference between the two energy levels considered,
is the difference between the two energy levels considered, ![]() .
.
Next, the necessary quantities are defined.
The components of the electric dipole matrix must have units of [![]() ]. But the geometry and the wavefunctions's length units are nanometers. So, to have the correct units, a factor of
]. But the geometry and the wavefunctions's length units are nanometers. So, to have the correct units, a factor of ![]() is introduced in the integral above. Also, note that
is introduced in the integral above. Also, note that ![]() is symmetrical.
is symmetrical.
The other parameters are defined.
A similar intensity as the one used in the work by Xie [Xie, 2009] will be used.
To plot the absorption, a factor of ![]() is used to have the
is used to have the ![]() axis be in meV.
axis be in meV.
In the latter plot, a peak in the optical absorption around the transition energy ![]() can be observed. This means that the system is better able to absorb optical waves with an energy that can promote the ground state to the first excited state. Also, the absorption has a maximum for a frequency that is in the terahertz range, which can be one of the characteristics to consider about this type of nanostructure in an optoelectronic application.
can be observed. This means that the system is better able to absorb optical waves with an energy that can promote the ground state to the first excited state. Also, the absorption has a maximum for a frequency that is in the terahertz range, which can be one of the characteristics to consider about this type of nanostructure in an optoelectronic application.
Variable Effective Mass Model Extension
In the previous approach, the effective mass of the electron in the ![]() quantum ring was used throughout the whole region. Although this procedure is widely used in the literature, a more appropriate way to solve the problem is to take into account the difference in effective mass in the ring region and the outside region. So, what is commonly known as a BenDaniel–Duke Hamiltonian [BenDaniel, 1966] is defined.
quantum ring was used throughout the whole region. Although this procedure is widely used in the literature, a more appropriate way to solve the problem is to take into account the difference in effective mass in the ring region and the outside region. So, what is commonly known as a BenDaniel–Duke Hamiltonian [BenDaniel, 1966] is defined.
To get the desired PDE operator, start from the momentum definition discussed earlier, ![]() , where
, where ![]() is the charge of the particle. Furthermore, to make the Hamiltonian be Hermitian, and given that the Hermitian conjugate of the product of three operators is
is the charge of the particle. Furthermore, to make the Hamiltonian be Hermitian, and given that the Hermitian conjugate of the product of three operators is ![]() , the following form in equation 8:
, the following form in equation 8:
Here, ![]() represents an operator. Then, equation 9:
represents an operator. Then, equation 9:
Now, the effective mass ![]() is a function of the position, however, still constant in each subregion. Thus, the effective mass will be a piecewise function.
is a function of the position, however, still constant in each subregion. Thus, the effective mass will be a piecewise function.
NDSolve can handle PDE coefficients that are position dependent. The only thing that needs to be done is to make use of the piecewise effective mass in the parameters pars, redefine the magnetic flux density and magnetic vector potential and generate a new Hamiltonian. The equation can be solved as before with the same geometry and mesh.
By default, a Hamiltonian with the diffusion term in the BenDaniel–Duke form is generated.
The boundary condition remains the same as before.
It is important to note that the energies have changed and are lower in magnitude than before. To see this more clearly, the energy eigenvalues for each approach are plotted.
Let's explore the difference between the probability densities for the model with constant effective mass with the ones in the BenDaniel–Duke approach.
Now, let's explore now what happens to the absorption.
The absorption behaves in a very similar manner as before. And maximum frequency has changed by an amount close to ![]()
![]() . To compare how the absorption has changed, the two results are plotted.
. To compare how the absorption has changed, the two results are plotted.
These graphs illustrate that there are not drastic changes in the absorption. Nevertheless, the absorption coefficients' maxima have decreased and a small redshift can be observed in the peak frequency when the difference in effective masses between regions is considered.
On the other hand, it is also interesting to explore the changes in the eigenfunctions. By looking at the plots of the wavefunctions for each approach, it is difficult to see any difference. Therefore, the integral of the product between an specific eigenstate considering constant effective mass and the same eigenstate considering variable effective mass is calculated.
The integrals are close to unity, which is expected when one calculates the integral of a given eigenstate squared, which makes one suspect that the eigenfunctions did not change much. Also, from the plot of the difference in the probability density for each approach it is clear that the functional form of the probability density stayed the same.
As a conclusion, it is possible to say that the changes in the energy eigenvalues are appreciable, close to ![]() of the energy of the ground state. The changes in the position of the absorption peak and the maximum absorption value are minor but noticeable. And this small change can be explained by looking at the eigenfunctions: their value and functional form did not change much. That means that the electric dipole moment matrix components did not undergo a huge change, and they are a big part of the absorption expressions used.
of the energy of the ground state. The changes in the position of the absorption peak and the maximum absorption value are minor but noticeable. And this small change can be explained by looking at the eigenfunctions: their value and functional form did not change much. That means that the electric dipole moment matrix components did not undergo a huge change, and they are a big part of the absorption expressions used.
For this problem, the use of the BenDaniel–Duke Hamiltonian may be dispensable if one is only interested in optical absorption, but its inclusion in the model can be essential for accurately calculating the energies.
References
1. García de Arquer, F. P., Talapin, D. v., Klimov, V. I., Arakawa, Y., Bayer, M. and Sargent, E. H. (2021). "Semiconductor Quantum Dots: Technological Progress and Future Challenges." Science, 373 (6555). https://doi.org/10.1126/science.aaz8541
2. Granados, D. and Garcia, J. M. (2003). "Customized Nanostructures MBE Growth: From Quantum Dots to Quantum Rings." Journal of Crystal Growth, 251 (1–4), 213–217. https://doi.org/10.1016/S0022-0248(02)02512-5
3. Cao, H., Deng, H., Ling, H., Liu, C., Smagley, V. A., Caldwell, R. B., Smolyakov, G. A., Gray, A. L., Lester, L. F., Eliseev, P. G. and Osiński, M. (2005). "Highly Unidirectional InAsInGaAsGaAs Quantum-Dot Ring Lasers." Applied Physics Letters, 86(20), 1–3. https://doi.org/10.1063/1.1931044
4. Yu, L. and Voskoboynikov, O. (2008). "Ballistic Aharonov–Bohm Quantum Bits and Quantum Gates." Solid State Communications, 145 (9–10), 447–450. https://doi.org/10.1016/J.SSC.2007.12.017
5. Gallardo, E., Martínez, L. J., Nowak, A. K., Sarkar, D., Sanvitto, D., van der Meulen, H. P., Calleja, J. M., Prieto, I., Granados, D., Taboada, A. G., García, J. M. and Postigo, P. A. (2010). "Single-Photon Emission by Semiconductor Quantum Rings in a Photonic Crystal." Journal of the Optical Society of America B, 27(6), A21. https://doi.org/10.1364/JOSAB.27.000A21
6. Fomin, V. M. (2014). Physiscs of Quantum Rings (Vladimir M Fomin, Ed.). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-39197-2
7. Xie, W. (2009). "Absorption Spectra of a Donor Impurity in a Quantum Ring." Physica Status Solidi (b), 246 (6), 1313–1317. https://doi.org/10.1002/pssb.200844349
8. Culchac, F. J., Porras-Montenegro, N. and Latgé, A. (2009). "Hydrostatic Pressure Effects on Electron States in GaAs–(Ga,Al)As Double Quantum Rings." Journal of Applied Physics, 105 (9), 094324. https://doi.org/10.1063/1.3124643
9. Ashcroft, N. W. and Mermin, N. D. (1976). Solid State Physics. Holt, Rinehart and Winston.
10. Zawadzki, W. (2020). "Wave and Uncertainty Properties of Electrons in Crystalline Solids." Physica Status Solidi (B) Basic Research, 257 (6). https://doi.org/10.1002/pssb.201900517
11. Chang, R., Potnis, S., Ramos, R., Zhuang, C., Hallaji, M., Hayat, A., Duque-Gomez, F., Sipe, J. E. and Steinberg, A. M. (2014). "Observing the Onset of Effective Mass." Physical Review Letters, 112 (17), 170404. https://doi.org/10.1103/PhysRevLett.112.170404
12. Duque-Gomez, F. and Sipe, J. E. (2012). "Response of a Particle in a One-Dimensional Lattice to an Applied Force: Dynamics of the Effective Mass." Physical Review A, 85 (5), 053412. https://doi.org/10.1103/PhysRevA.85.053412
13. Kohn, W. and Sham, L. J. (1965). "Self-Consistent Equations Including Exchange and Correlation Effects." Physical Review, 140 (4A), A1133–A1138. https://doi.org/10.1103/PhysRev.140.A1133
14. Harrison, P. (2005). Quantum Wells, Wires and Dots. John Wiley Sons, Ltd. https://doi.org/10.1002/0470010827
15. Hernández, N., López-Doria, R. A., Rivera, I. E. and Fulla, M. R. (2022). "Refractive Index Change of a D+2 Complex in GaAs/AlxGa1−xAs Quantum Ring." Journal of Materials Science, 57 (18), 8417–8424. https://doi.org/10.1007/s10853-021-06763-8
16. Jahan, K. L., Boda, A., Shankar, I. v., Raju, Ch. N. and Chatterjee, A. (2018). "Magnetic Field Effect on the Energy Levels of an Exciton in a GaAs Quantum Dot: Application for Excitonic Lasers." Scientific Reports, 8 (1), 5073. https://doi.org/10.1038/s41598-018-23348-9
17. Gutiérrez, W., García, L. F. and Mikhailov, I. D. (2010). "Coupled Donors in Quantum Ring in a Threading Magnetic Field." Physica E: Low-Dimensional Systems and Nanostructures, 43 (1), 559–566. https://doi.org/https://doi.org/10.1016/j.physe.2010.09.015
18. Fomin, V. M. (2018). "Quantum Ring: A Unique Playground for the Quantum-Mechanical Paradigm," Physics of Quantum Rings. NanoScience and Technology (V. Fomin, ed.), Springer, Cham. https://doi.org/10.1007/978-3-319-95159-1_1
19. Luttinger, J. M. (1951). "The Effect of a Magnetic Field on Electrons in a Periodic Potential." Physical Review, 84 (4), 814–817. https://doi.org/10.1103/PhysRev.84.814
20. Peierls, R. (1997). "On the Theory of the Diamagnetism of Conduction Electrons" (pp. 97–120), Selected Scientific Papers of Sir Rudolf Peierls (R. H. Dalitz and R. Peierls, eds.). World Scientific. https://doi.org/10.1142/9789812795779_0010
21. Feynman, R. P., Leighton, R. B. and Sands, M. (1965). The Feynman Lectures on Physics. Vol. 3. Addison-Wesley. ISBN 0-201-02115-3. https://www.feynmanlectures.caltech.edu/III_12.html#Ch12-S4
22. Cohen-Tannoudji, B. Diu and F. Laloe, “Quantum Mechanics,” John Wiley & Sons, New York, 1977, (Vol. 1), p.409.
23. Karabulut, İ., Ünlü, S. and Şafak, H. (2005). "Calculation of the Changes in the Absorption and Refractive Index for Intersubband Optical Transitions in a Quantum Box." Physica Status Solidi (b), 242(14), 2902–2909. https://doi.org/10.1002/pssb.200541093
24. BenDaniel, D. J. and Duke, C. B. (1966). "Space-Charge Effects on Electron Tunneling." Physical Review, 152 (2), 683–692. https://doi.org/10.1103/PhysRev.152.683