ARCHProcess

ARCHProcess[κ,{α1,…,αq}]

標準ホワイトノイズに駆動される q 次ARCH（自己回帰条件付き分散不均一）過程を表す．

ARCHProcess[κ,{α1,…,αq},init]

初期データが init であるARCH過程を表す．

詳細

  • ARCHProcessは，離散時間・連続状態のランダム過程である．
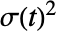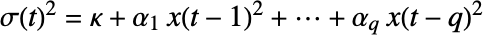  • 条件付き平均Expectation[x[t] {x[t-1], …}]=0およびExpectation [x[t]2{x[t-1, …}]で与えられる条件付き分散 が方程式 を満足するのであれば，過程 x[t] はARCH過程である．
  • 初期データ init は，リスト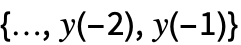{...,y(-2),y(-1)}として，あるいはタイムスタンプが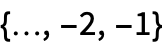{...,-2,-1}であると了解される単一路TemporalDataオブジェクトとして与えることができる．
  • スカラーARCH過程は非負の係数 αiおよび正の係数 κ を持つことができる．
  • ARCHProcess[q]は，EstimatedProcessおよび関連関数で使われる q 次ARCH過程を表す．
  • ARCHProcessは，RandomFunction，CovarianceFunction，TimeSeriesForecast等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

ARCHProcessのシミュレーションを行う：

弱定常過程の無条件平均値関数および無条件分散関数：

固定した初期値で：

観測は無相関であるが依存する：

データの平方値には相関関係がある：

スコープ  (13)

基本例題  (8)

経路の集合のシミュレーションを行う：

任意精度でシミュレーションを行う：

指定された初期値で弱定常過程のシミュレーションを行う：

非弱定常過程の場合：

和分ARCHProcess：

爆発ARCHProcess：

そのような過程は二次定常ではない：

ARCHProcessが共分散定常になるための条件：

ARCHProcess[2]の二次定常性の範囲：

ARCHProcessを推定する：

条件付き最尤推定を使う：

予測する：

20ステップ先の予測を求める：

予測の平均二乗誤差を求める：

予測状態は0に等しい．したがって，予測される標準偏差境界は以下の通りである：

平均二乗誤差とともにこの値をプロットする：

過程スライス特性  (5)

次数1の弱定常ARCHのモーメント：

指定された初期条件によるARCH過程のモーメント：

歪度：

尖度：

尖度が定義されている領域：

スライス分布のシミュレーションを行う：

サンプルの確率密度関数：

モンテカルロ法を使い，スライス分布についてのNProbabilityを計算する：

NExpectationを計算する：

二次Momentと比較する：

特性と関係  (3)

ARCHProcessの値は無相関である：

対応するARProcess：

初期値が指定された過程について：

ARCHProcessの値を平方したものはARProcessに従う：

平方値のCorrelationFunctionおよびPartialCorrelationFunction：

対応する自己回帰過程：

自己回帰過程のCorrelationFunctionおよびPartialCorrelationFunction：

Wolfram Research (2014), ARCHProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/ARCHProcess.html.

テキスト

Wolfram Research (2014), ARCHProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/ARCHProcess.html.

CMS

Wolfram Language. 2014. "ARCHProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ARCHProcess.html.

APA

Wolfram Language. (2014). ARCHProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ARCHProcess.html

BibTeX

@misc{reference.wolfram_2024_archprocess, author="Wolfram Research", title="{ARCHProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ARCHProcess.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_archprocess, organization={Wolfram Research}, title={ARCHProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/ARCHProcess.html}, note=[Accessed: 22-November-2024 ]}