AbelianGroup

AbelianGroup[{n1,n2,…}]

represents the direct product of the cyclic groups of degrees n1,n2,….

Details

  • The degrees ni of AbelianGroup[{n1,n2,…}] must be non-negative integers.
  • AbelianGroup[{n1,n2,…}] is represented by default as a permutation group on the points {1,…,n1+n2+…}.

Background & Context

  • AbelianGroup[{n1,n2,…,nk}] represents the commutative group defined as the direct product 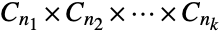of cyclic groups having non-negative integer degrees n1,n2,…,nk. Here, the direct product of groups 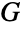, , 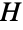… is the analog of the Cartesian product of sets in which the underlying sets are ordered tuples 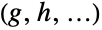with 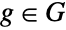, , 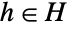… and the group operation is taken componentwise so that .
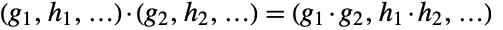  • In general, the term "Abelian group" is used to refer to a group that is commutative, i.e. a group 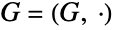for which the group operation satisfies the identity 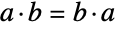for all elements 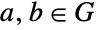. The fundamental theorem of finite Abelian groups states that every finite Abelian group can be expressed as a direct product of cyclic groups. As a result, the function AbelianGroup can be used to represent any finite Abelian group.
  • The default representation of AbelianGroup[{n1,n2,…,nk}] is as a permutation group on the elements 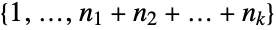. When 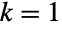, AbelianGroup[{n}] is equivalent to CyclicGroup[n] (with both AbelianGroup[{0}] and AbelianGroup[{1}] equivalent to the trivial group with exactly one element).
  • The usual group theoretic functions may be applied to AbelianGroup[{n1,n2,…,nk}], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the Abelian group AbelianGroup[{n1,n2,…,nk}] are available via FiniteGroupData[{"AbelianGroup",{n1,n2,…,nk}},"prop"].
  • AbelianGroup is related to a number of other symbols. Mathematically, AbelianGroup[{n1,n2,…,nk}] is equivalent to the direct product of the groups CyclicGroup[n1],CyclicGroup[n2],…,CyclicGroup[nk]. Other infinite families of finite groups built into the Wolfram Language that are parametrized by integers include AlternatingGroup, CyclicGroup, DihedralGroup and SymmetricGroup.

Examples

open allclose all

Basic Examples  (3)

Number of elements of an Abelian group:

Permutation generators of an Abelian group:

Elements of a permutation representation of an Abelian group:

Scope  (1)

Direct product of any number of cyclic groups of any degrees:

Properties & Relations  (2)

For nonzero degrees, the order of AbelianGroup[{n1,n2,…}] is the product of the ni:

A group AbelianGroup[{p,p,…}] with p prime is called an elementary Abelian group. In such groups all nontrivial elements have order p:

Neat Examples  (1)

The Cayley graph of the direct product of two cyclic groups resembles a torus:

Wolfram Research (2010), AbelianGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/AbelianGroup.html.

Text

Wolfram Research (2010), AbelianGroup, Wolfram Language function, https://reference.wolfram.com/language/ref/AbelianGroup.html.

CMS

Wolfram Language. 2010. "AbelianGroup." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AbelianGroup.html.

APA

Wolfram Language. (2010). AbelianGroup. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AbelianGroup.html

BibTeX

@misc{reference.wolfram_2024_abeliangroup, author="Wolfram Research", title="{AbelianGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AbelianGroup.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_abeliangroup, organization={Wolfram Research}, title={AbelianGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/AbelianGroup.html}, note=[Accessed: 21-December-2024 ]}